Ferramentas Matemáticas para Computação Científica: mudanças entre as edições
imported>Fargoud |
imported>Fargoud |
||
| Linha 16: | Linha 16: | ||
<center> ⇒ MEMÓRIA </center> | <center> ⇒ MEMÓRIA </center> | ||
[[image: FMCmemoria.png|center]] | |||
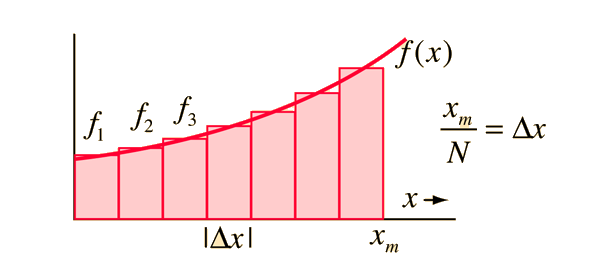
Um cálculo como o da integral, por exemplo, seria impossível, porque nenhum computador teria memória suficiente para armazenar infinitos valores. | Um cálculo como o da integral, por exemplo, seria impossível, porque nenhum computador teria memória suficiente para armazenar infinitos valores. | ||
| Linha 25: | Linha 27: | ||
[[image: FMCintegralnumerica.png|center]] | [[image: FMCintegralnumerica.png|center]] | ||
=Cálculo "humano" x Cálculo numérico= | =Cálculo "humano" x Cálculo numérico= | ||
Edição das 14h15min de 13 de março de 2019
Palestra apresentada durante a Semana Científica do Curso de Engenharia Elétrica Campus Itajaí - março de 2019 Profa. Fernanda Argoud da Silva, M.Sc., Dr. Eng.
Introdução
O computador é uma ferramenta indispensável para o avanço da Ciência.
Apesar de ter que ser programado, é capaz de executar cálculos complexos e/ou repetitivos, em uma velocidade muito maior que qualquer ser humano e sem desgaste ou cansaço.
Porém, tem uma limitação muito severa:
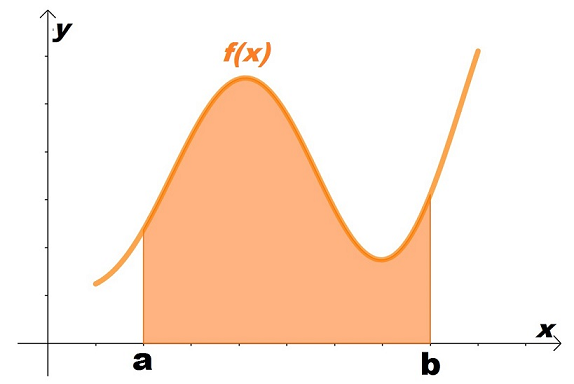
Um cálculo como o da integral, por exemplo, seria impossível, porque nenhum computador teria memória suficiente para armazenar infinitos valores.
A solução, então, é discreta e numérica.
Cálculo "humano" x Cálculo numérico
Os algoritmos para cálculos científicos e matemáticos normalmente são específicos.
NÃO são procedimentos de resolução "humana" adaptados à uma linguagem de programação.
Cálculo de raízes de equação
Raízes de uma equação y = f(x) → Quais são os valores de x que levam à equação y ao valor ZERO??
Em outras palavras: em que pontos de x a função atravessa o eixo y = 0?
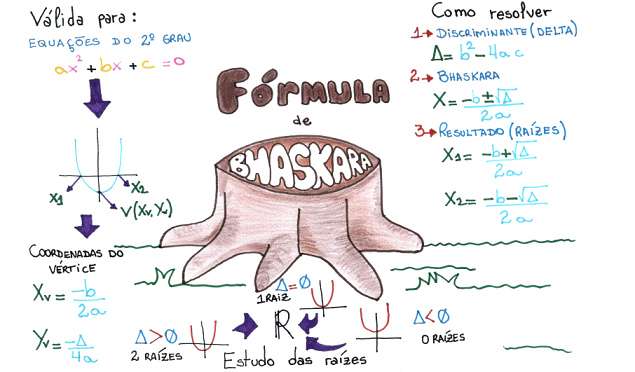
Métodos "humanos"
- Bhaskara ⇒ Baseado no uso dos coeficientes da equação:
- Para equações de terceiro grau:
Seja a equação da forma a.x³ + b.x² + c.x + d = a.(x - r1).(x - r2).(x - r3)
Mais informações: Relações de Girardi...
- Para equações de quarto grau:
...
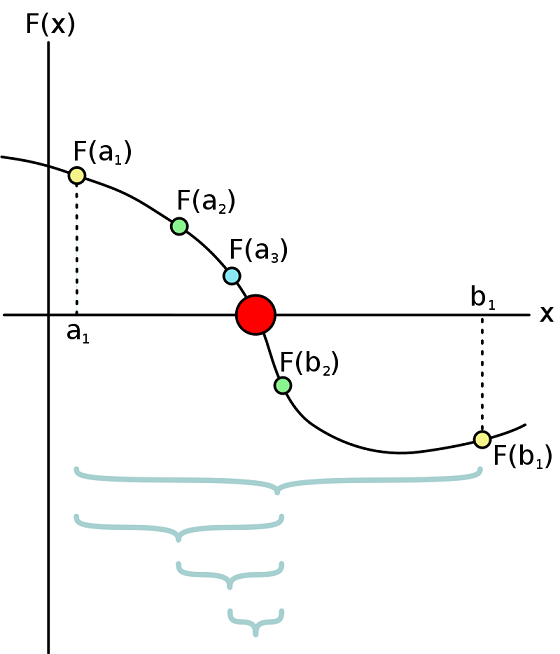
Método numérico - Bissecção
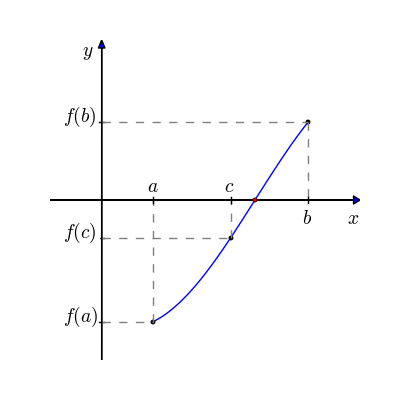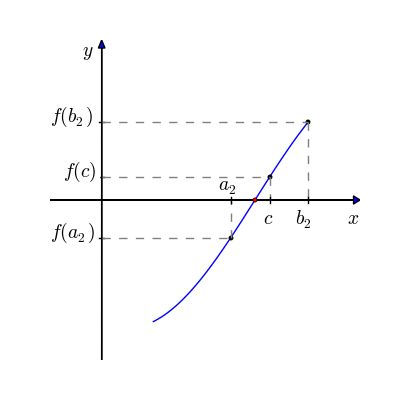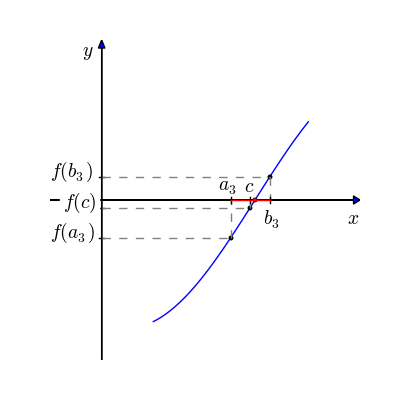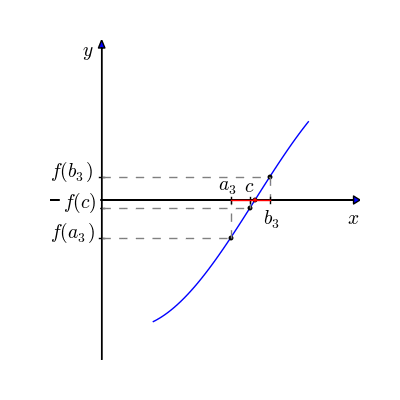
O método da bissecção é um método de busca de raízes que divide repetidamente um intervalo da função e então seleciona um subintervalo contendo a raiz para processamento adicional. Escolhe-se dois pontos extremos, a e b, de preferência para os quais haja um inversão de polaridade da curva.
é usado frequentemente para obter uma primeira aproximação de uma solução, a qual é então utilizada como ponto inicial para métodos que convergem mais rapidamente.
Trata-se de um método simples e robusto, relativamente lento quando comparado a métodos como o método de Newton ou o método das secantes.
PSEUDOCÓDIGO:
ENTRADA: Função f,
extremos do intervalo a, b,
tolerância TOL,
número máximo de iterações NMAX
CONDIÇÕES: a < b, ou f(a) < 0 e f(b) > 0 ou f(a) > 0 e f(b) < 0
SAÍDA: valor que difere de uma raiz de f(x)=0 por menos do que TOL
N ← 1
Enquanto N ≤ NMAX # limita o número de iterações para prevenir um loop infinito
c ← (a + b)/2 # novo ponto médio
Se f(c) = 0 or (b – a)/2 < TOL então # solução encontrada
Retorne(c)
Pare
Fim
N ← N + 1 # incrementa o contador de iterações
Se sinal(f(c)) = sinal(f(a)) então a ← c senão b ← c # novo intervalo
Fim
Retorne("O algoritmo falhou.") # núm. máximo de iterações excedido