Solução Exercício 2 - RESISTORES

Exercício sobre especificação de bitola de fio

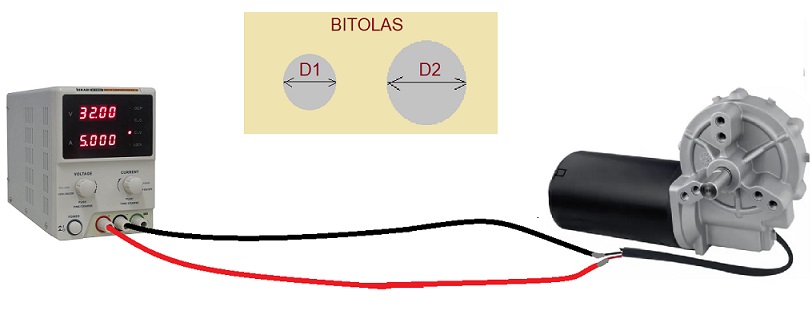
Qual dos cabos de cobre abaixo deve ser usado, o de D1 = 1 mm, ou o de D2 = 2mm, para garantir uma corrente acima de 10 A, se a tensão fornecida for de 32 V, para um circuito cujo comprimento total dos cabos é de 200 m?

Considere π = 3,1416 e ρ_cobre = 1,7.10 ^-8 Ω.m

---

Resolução

Em primeiro lugar, temos que entender que, para que a carga seja ultrapassada por uma corrente de, no mínimo, 10A, significa que a resistênca deva ser dada por:

 V = R.I , e  I ≥ 10
 ⇒  I = V/ R ≥ 10
 ⇒  V/R ≥ 10
 ⇒  32 ≥ R. 10
 ⇒  32/10 ≥ R
 ⇒  3,2 ≥ R
 ou
 ⇒  R ≤ 3,2 Ω

Ou seja, qualquer resistência total de cabo maior que 3,2 Ω vai gerar uma corrente menor que 10 A.

Logicamente, agora temos que investigar os valores das resistências para ambas as bitolas de cabo, e verificar qual(is) atenderá(ão) a exigência acima.

A área S1 de seção do primeiro cabo, de D1 = 1 mm = 0,001 m é dada por:

S1 = π. D1²/4
S1 = 3,1416 . 0,001² / 4
S1 = 7,854 .10-7 m²

Logo:

R1 = ρ . l/S1
R1 = 1,7.10-8 . 200/7,854.10-7
R1 = 4,33 Ω

Repetindo o procedimento para o segundo tipo de cabo:

S2 = π. D2²/4
S2 = 3,1416 . 0,002² / 4
S2 = 3,1416 .10-6 m²

Logo:

R2 = ρ . l/S2
R2 = 1,7.10-8 . 200/3,1416.10-6
R2 = 1,08 Ω

Assim, o segundo resistor, de diâmetro D2, é o que vai atender à exigência colocada.

<< Voltar para os Exercícios