Exercícios Circuitos Aritméticos: mudanças entre as edições
Ir para navegação
Ir para pesquisar
imported>Fargoud |
imported>Fargoud Sem resumo de edição |
||
| (Uma revisão intermediária pelo mesmo usuário não está sendo mostrada) | |||
| Linha 17: | Linha 17: | ||
# Calcule as subtrações binárias abaixo, em 8 bits: | # Calcule as subtrações binárias abaixo, em 8 bits: | ||
45d - 23d = 0010 1101 + C2(0001 0111) = 0010 1101 + 1110 1001 = | 45d - 23d = 0010 1101 + C2(0001 0111) = 0010 1101 + 1110 1001 = 1 0001 0110, despreza o 9o bit: 0001.0110 = +22d | ||
103d - 25d = | 103d - 25d = 0110 0111 + C2(0001 1001) = 0110 0111 + 1110 0111 = 1 0100 1110, despreza o 9o bit: 0100 1110 = +78d | ||
-99d + 10d | -99d + 10d = C2(0110 0011) + 0000 1010 = 1001 1101 + 0000 1010 = 1010 0111, aplicando C2: 0101 1001 = -89d | ||
-68d - 47d | -68d - 47d = C2(0100 0100) + C2(0010 1111) = 1011 1100 + 1101 0001 = 1 1000 1101, despreza o 9o bit e aplica C2: 0111 0011 = -115 | ||
Edição atual tal como às 17h51min de 7 de fevereiro de 2022
Respostas Exercícios Circuitos Aritméticos
- Calcule as somas binárias abaixo, para qualquer número de bits:
1011b + 0101b = 10000b 010110b + 1110b = 100100b 01001110b + 11000011b = 0100010001b
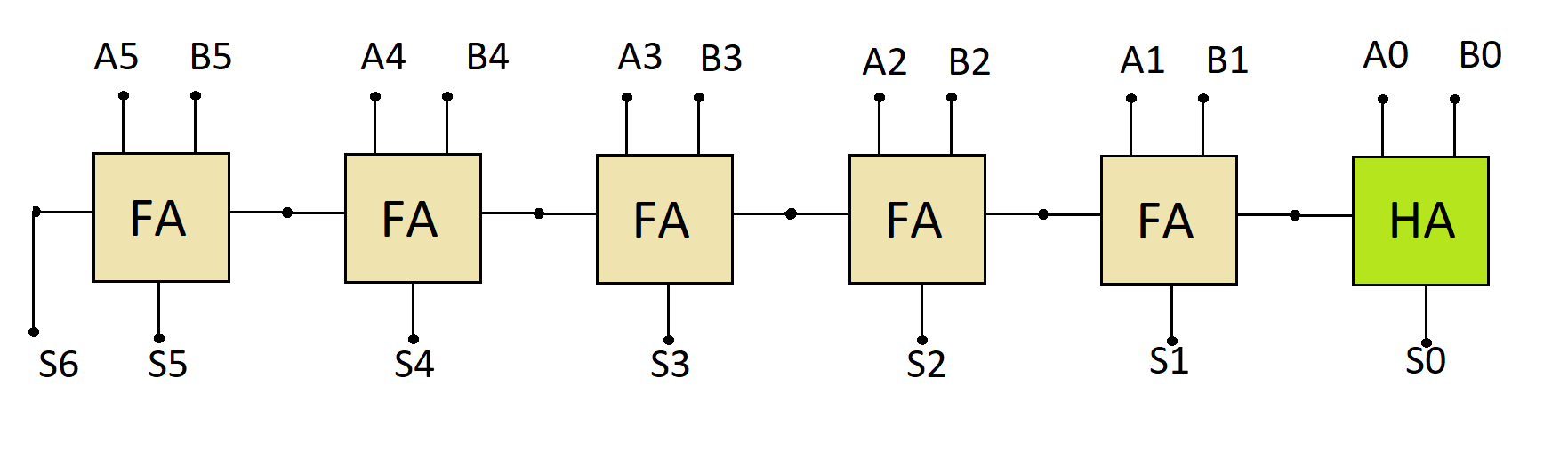
- Desenhe, usando blocos meio-somador e somador completo, um circuito somador para palavras de 6 bits:
- Calcule o complemento 2 dos números abaixo:
57d = 32 + 16 + 8 + 1= 0111001b, C2(0111001b) = 100 0111b 120d = 64 + 32 + 16 + 8 = 0111 1000b , C2(0111 1000b) = 1000 1000b 405d = 256 + 128 + 16 + 4 + 1 = 01 1001 0101b , C2(01 1001 0101) = 10 0110 1011b 1237d = 1024 + 128+ 64+ 16+ 4 + 1 = 0100 1101 0101b, C2(0100 1101 0101) = 1011 0010 1011b
- Calcule as subtrações binárias abaixo, em 8 bits:
45d - 23d = 0010 1101 + C2(0001 0111) = 0010 1101 + 1110 1001 = 1 0001 0110, despreza o 9o bit: 0001.0110 = +22d 103d - 25d = 0110 0111 + C2(0001 1001) = 0110 0111 + 1110 0111 = 1 0100 1110, despreza o 9o bit: 0100 1110 = +78d -99d + 10d = C2(0110 0011) + 0000 1010 = 1001 1101 + 0000 1010 = 1010 0111, aplicando C2: 0101 1001 = -89d -68d - 47d = C2(0100 0100) + C2(0010 1111) = 1011 1100 + 1101 0001 = 1 1000 1101, despreza o 9o bit e aplica C2: 0111 0011 = -115