Solex3cap11: mudanças entre as edições

De IFSC
Ir para navegação Ir para pesquisar
imported>Fargoud
Sem resumo de edição
imported>Fargoud
Sem resumo de edição
 
(10 revisões intermediárias pelo mesmo usuário não estão sendo mostradas)
Linha 1: Linha 1:
*  CARGA MOTOR:  
*  CARGA MOTOR:  


Potência aparente S = V.I = 1,5 KVA e potência ativa P = V. I. cosφ = 1,2 KW
Sabe-se que a Potência aparente é igual a S = V.I e foi dada por:


Portanto:
S<sub>motor</sub> = 1,5 KVA
            cos &phi;<sub>motor</sub> = P<sub>motor</sub>/S<sub>motor</sub> = 1,5 K/1,2K = 0,8  &rarr; &phi; = 36,87&deg;


E
Também, sabe-se que a potência ativa P = V. I. cos&phi; e que foi dada por
    Q<sub>motor</sub> = S.sen &phi;<sub>motor</sub> = 1,5K x 0,6 = 0,9 KVar
P<sub>motor</sub> = 1,2 KW


Portanto, cos &phi;<sub>motor</sub> = P<sub>motor</sub>/S<sub>motor</sub>  = 1,5 K/1,2K = 0,8  &rarr;


&phi;<sub>motor</sub> = 36,87&deg;


e Q<sub>motor</sub> = S.sen &phi;<sub>motor</sub> = 1,5K x 0,6 :


  Q<sub>motor</sub> =  0,9 KVar


Portanto:


a) corrente de entrada da resistência
*  CARGA LÂMPADAS:
 
Se foi dada em watts, significa que se trata da potência ativa. Portanto, a carga total de lâmpadas = 10 x 60W :
 
P<sub>lamp</sub> = 600 W
 
, com  cos &phi;<sub>lamp</sub> = 0,6 e, portanto cos<sup>-1</sup> 0,6 = 53,13 :
 
  &phi;<sub>lamp</sub> = 53,13&deg;
 
 
Como P<sub>lamp</sub> = S.cos &phi; &rarr; S = P<sub>lamp</sub>/cos &phi;:
 
S<sub>lamp</sub> = 1000 VA
 
e Q<sub>lamp</sub> = S.sen &phi;:
 
Q<sub>lamp</sub> = 800 Var
 


  I= P/(V.cos&phi;)
  I=9000/[220.0.8]= 51,14 A


B) Potência aparente
*  CARGA TOTAL:


  S = V.I = 220.51,14 = 11,250 kVA
Os triângulos do circuitos são:


B) Potência reativa
  [[image: ex3Cap11.png|center]]


  Q = (S&sup2;-P&sup2;)&frac12; = (11,25&sup2; - 9&sup2;)&frac12; = 6,75 kVAr
Fazendo-se as somas:


    P<sub>total</sub> = P<sub>motor</sub> +  P<sub>lamp</sub> = 1200 + 600 = 1,8 KW
    Q<sub>total</sub> = Q<sub>motor</sub> +  Q<sub>lamp</sub> = 900 + 800 = 1,7 kVar


Portanto:
Portanto:


a) corrente de entrada da resistência
    S<sub>total</sub> = (P<sub>total</sub><sup>2</sup> +  Q<sub>total</sub><sup>2</sup>)<sup>1/2</sup>
 
    S<sub>total</sub> = 2,476 KVA
  I= P/(V.cos&phi;)
  I=9000/[220.0.8]= 51,14 A


B) Potência aparente
e
    &phi;<sub>total</sub> = arc tg (Q/P) = 43,36&deg;


  S = V.I = 220.51,14 = 11,250 kVA


B) Potência reativa
A correção do fator de potência implicaria no uso de uma carga capacitiva com Q = -1,7 KVar.


  Q = (S&sup2;-P&sup2;)&frac12; = (11,25&sup2; - 9&sup2;)&frac12; = 6,75 kVAr
[https://wiki.ifsc.edu.br/mediawiki/index.php/AULA_8_-_Circuitos_El%C3%A9tricos_2_-_Gradua%C3%A7%C3%A3o#Exerc.C3.ADcios  << Voltar]

Edição atual tal como às 15h43min de 10 de junho de 2025

  • CARGA MOTOR:

Sabe-se que a Potência aparente é igual a S = V.I e foi dada por: 

Smotor = 1,5 KVA

Também, sabe-se que a potência ativa P = V. I. cosφ e que foi dada por 

Pmotor = 1,2 KW

Portanto, cos φmotor = Pmotor/Smotor = 1,5 K/1,2K = 0,8 → 

φmotor = 36,87°

e Qmotor = S.sen φmotor = 1,5K x 0,6 : 

 Qmotor =  0,9 KVar


  • CARGA LÂMPADAS:

Se foi dada em watts, significa que se trata da potência ativa. Portanto, a carga total de lâmpadas = 10 x 60W : 

Plamp = 600 W

, com cos φlamp = 0,6 e, portanto cos-1 0,6 = 53,13 : 

 φlamp = 53,13°

Como Plamp = S.cos φ → S = Plamp/cos φ: 

Slamp = 1000 VA

e Qlamp = S.sen φ: 

Qlamp = 800 Var


  • CARGA TOTAL:

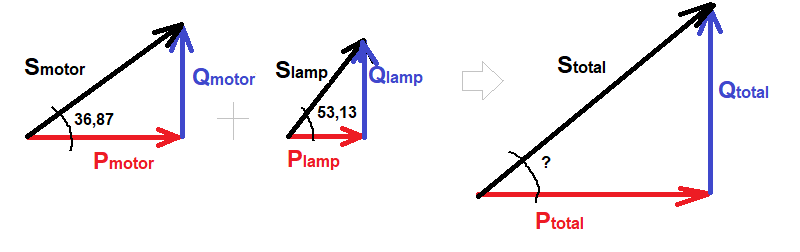
Os triângulos do circuitos são:

Ex3Cap11.png

Fazendo-se as somas: 

    Ptotal = Pmotor +  Plamp = 1200 + 600 = 1,8 KW 
    Qtotal = Qmotor +  Qlamp = 900 + 800 = 1,7 kVar

Portanto: 

    Stotal = (Ptotal2 +  Qtotal2)1/2
    Stotal = 2,476 KVA

e 

    φtotal = arc tg (Q/P) = 43,36°


A correção do fator de potência implicaria no uso de uma carga capacitiva com Q = -1,7 KVar.

<< Voltar

Disponível em “https://wiki.ifsc.edu.br/index.php?title=Solex3cap11&oldid=24295”