Ferramentas Matemáticas para Computação Científica: mudanças entre as edições
imported>Fargoud |
imported>Fargoud |
||
| Linha 19: | Linha 19: | ||
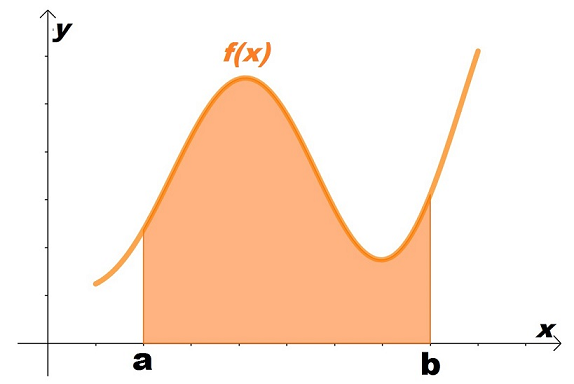
Um cálculo como o da integral, por exemplo, seria impossível, porque nenhum computador teria memória suficiente para armazenar infinitos valores. | Um cálculo como o da integral, por exemplo, seria impossível, porque nenhum computador teria memória suficiente para armazenar infinitos valores. | ||
[[image: | [[image: FMCintegr.png| center]] | ||
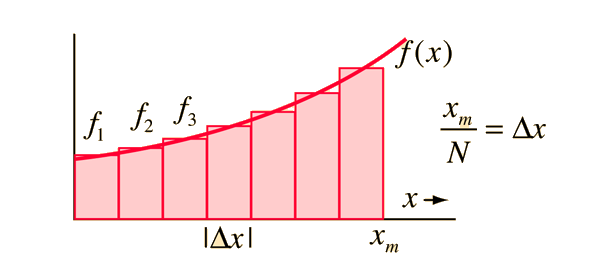
A solução, então, é ''discreta'' e ''numérica''. | A solução, então, é ''discreta'' e ''numérica''. | ||
[[image: FMCintegralnumerica.png|center]] | [[image: FMCintegralnumerica.png|center]] | ||
=Cálculo "humano" x Cálculo numérico= | |||
Os algoritmos para cálculos científicos e matemáticos normalmente são específicos. | |||
NÃO são procedimentos de resolução "humana" adaptados à uma linguagem de programação. | |||
==Cálculo de raízes de equação== | |||
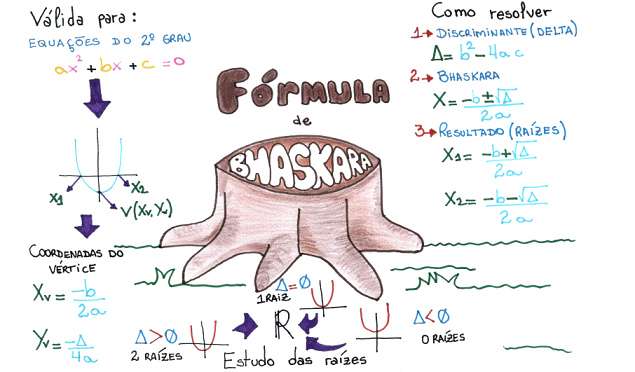
===Método "humano" - ''Bhaskara''=== | |||
[[image: FMCbhask.png|center]] | |||
===Método numérico - Bissecção === | |||
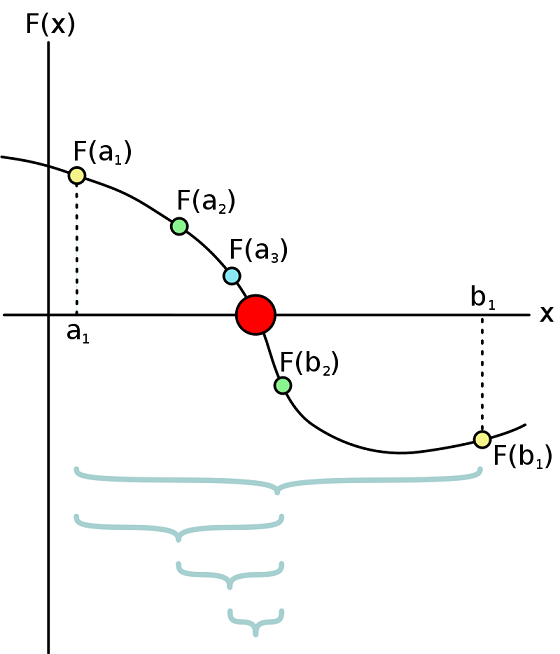
O '''método da bissecção''' é um método de busca de raízes que divide repetidamente um intervalo da função e então seleciona um subintervalo contendo a raiz para processamento adicional. | |||
[[image: FMCbissec.png|center]] | |||
é usado frequentemente para obter uma primeira aproximação de uma solução, a qual é então utilizada como ponto inicial para métodos que convergem mais rapidamente. | |||
Trata-se de um método simples e robusto, relativamente lento quando comparado a métodos como o método de Newton ou o método das secantes. | |||
Edição das 11h41min de 13 de março de 2019
Palestra apresentada durante a Semana Científica do Curso de Engenharia Elétrica Campus Itajaí - março de 2019 Profa. Fernanda Argoud da Silva, M.Sc., Dr. Eng.
Introdução
O computador é uma ferramenta indispensável para o avanço da Ciência.
Apesar de ter que ser programado, é capaz de executar cálculos complexos e/ou repetitivos, em uma velocidade muito maior que qualquer ser humano e sem desgaste ou cansaço.
Porém, tem uma limitação muito severa:
Um cálculo como o da integral, por exemplo, seria impossível, porque nenhum computador teria memória suficiente para armazenar infinitos valores.
A solução, então, é discreta e numérica.
Cálculo "humano" x Cálculo numérico
Os algoritmos para cálculos científicos e matemáticos normalmente são específicos.
NÃO são procedimentos de resolução "humana" adaptados à uma linguagem de programação.
Cálculo de raízes de equação
Método "humano" - Bhaskara
Método numérico - Bissecção
O método da bissecção é um método de busca de raízes que divide repetidamente um intervalo da função e então seleciona um subintervalo contendo a raiz para processamento adicional.
é usado frequentemente para obter uma primeira aproximação de uma solução, a qual é então utilizada como ponto inicial para métodos que convergem mais rapidamente.
Trata-se de um método simples e robusto, relativamente lento quando comparado a métodos como o método de Newton ou o método das secantes.