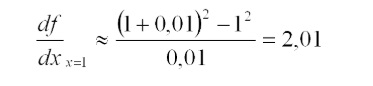Ferramentas Matemáticas para Computação Científica
Palestra apresentada durante a Semana Científica do Curso de Engenharia Elétrica Campus Itajaí - março de 2019 Profa. Fernanda Argoud da Silva, M.Sc., Dr. Eng.
Introdução
O computador é uma ferramenta indispensável para o avanço da Ciência.
Apesar de ter que ser programado, é capaz de executar cálculos complexos e/ou repetitivos, em uma velocidade muito maior que qualquer ser humano e sem desgaste ou cansaço.
Porém, tem uma limitação muito severa:
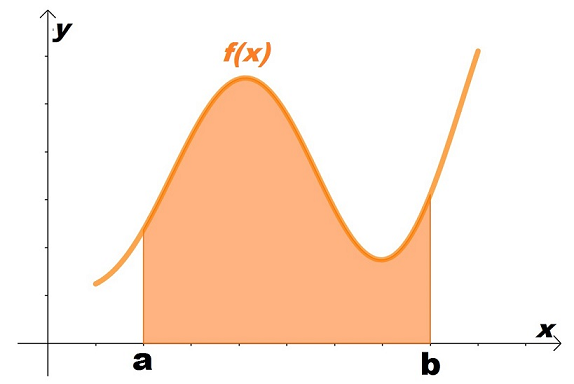
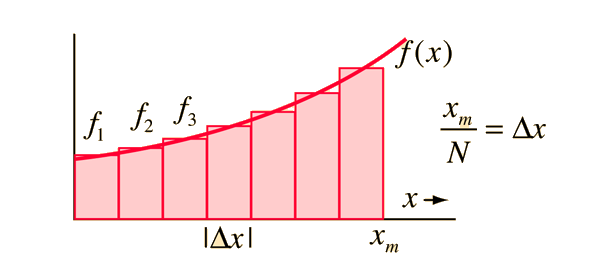
Um cálculo como o da integral, por exemplo, seria impossível, porque nenhum computador teria memória suficiente para armazenar infinitos valores.
A solução, então, é discreta e numérica.
Obviamente, a solução sempre será aproximada, jamais exata.
É importante, então, estabelecer um erro máximo admitido.
Cálculo "humano" x Cálculo numérico
Os algoritmos para cálculos científicos e matemáticos normalmente são específicos.
NÃO são procedimentos de resolução analítica, ou "humana", adaptados à uma linguagem de programação.
São procedimentos numéricos (iterativos) específicos, desenvolvidos com o objetivo de facilitar a resolução pelo computador e no menor tempo possível.
Cálculo de derivada de função
Derivada de uma função é o cálculo da inclinação desta função, em cada ponto da curva.
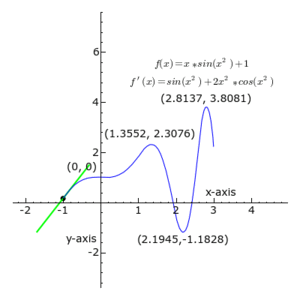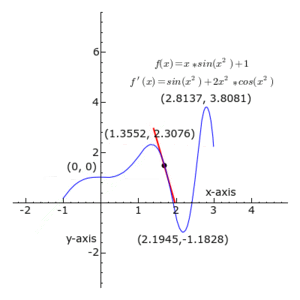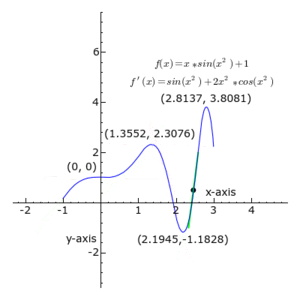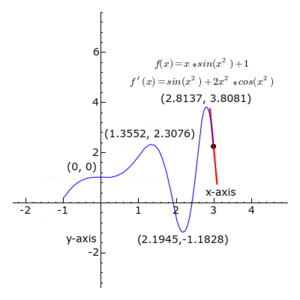
Em cada ponto, a derivada de f(x)= 1 + x.sin x², que é igual a f ' (x)= sin x² + 2.x².cos x² é a tangente do ângulo que a reta tangente à curva faz em relação ao eixo das abscissas.
A reta é sempre tangente à curva azul; a tangente do ângulo que ela faz com o eixo das abscissas é a derivada.
Note-se que a derivada é positiva quando verde, negativa quando vermelha, e zero quando preta.
Solução analítica
A determinação analítica de uma derivada de função pode ser bastante complexa.
Tomemos como exemplo a resolução da derivada da função f(x) = x², no ponto x = 1.
Por definição, a derivada é o diferencial entre um ponto da função, e outro, localizado a uma distância h infinitesimal (tendendo a zero). Portanto, será:
Para uma função muito simples, como f(x) = x², são necessários vários cálculos literais, indefinidos e de limite.
Em computador, é muitíssimo complicado ensinar a máquina a compreender "limites" tendendo a zero, ou a infinito. Provavelmente, teria que ser criado um banco de dados de casos mais frequentes.
Ainda, depois de se obter a correspondente função derivada, ainda é necessário calcular-se o valor desta, no ponto específico x = 1.
Solução numérica
Uma solução numérica, ainda que inexata, pode ser tremendamente mais simples.
Pode-se reduzir a substituir o valor de x = 1 na equação de cálculo da derivada, adotando como h um valor suficientemente pequeno (conceito do δ da derivada), tal como h = 0,01.
O cálculo matemático total seria:
E teríamos a resposta com um erro relativo percentual de:
Erro % = (aprox - correto)/correto x 100
Erro % = (2,01 - 2)/2 x 100
Erro % = 0,5%
Cálculo de raízes de equação
Raízes de uma equação y = f(x) → Quais são os valores de x que levam à equação y ao valor ZERO??
Em outras palavras: em que pontos de x a função atravessa o eixo y = 0?
Métodos "humanos" ou analíticos
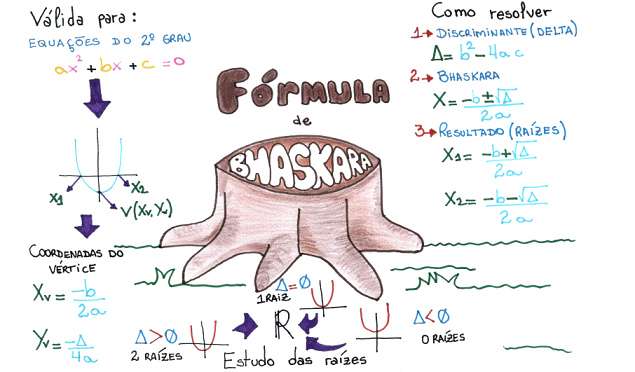
- Para equações de 2o. grau: Bhaskara ⇒ Baseado no uso dos coeficientes da equação:
- Para equações de terceiro grau:
Seja a equação da forma a.x³ + b.x² + c.x + d = a.(x - r1).(x - r2).(x - r3)
Mais informações: Relações de Girardi...
- Para equações de quarto grau: Equações quárticas ou biquadradas
...
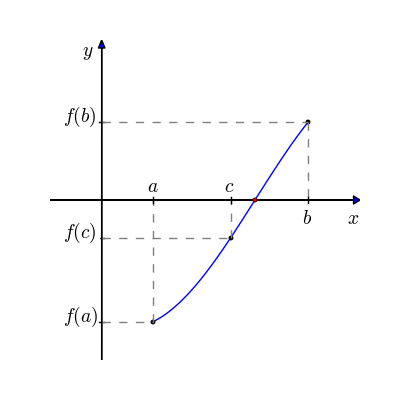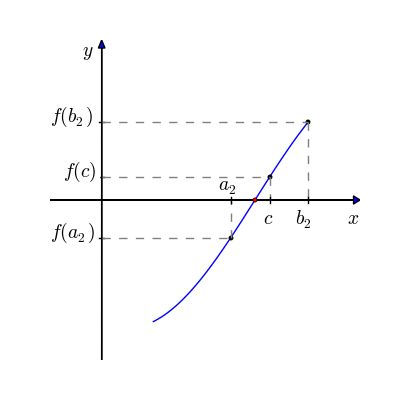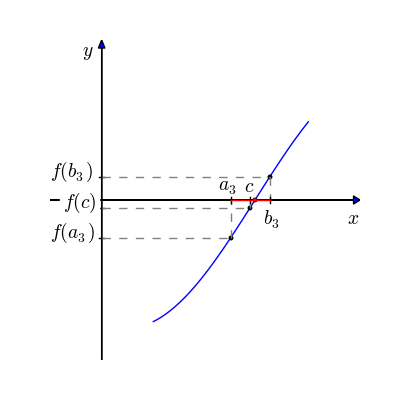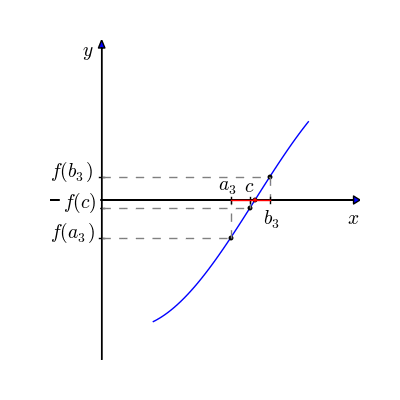
Método numérico - Bissecção
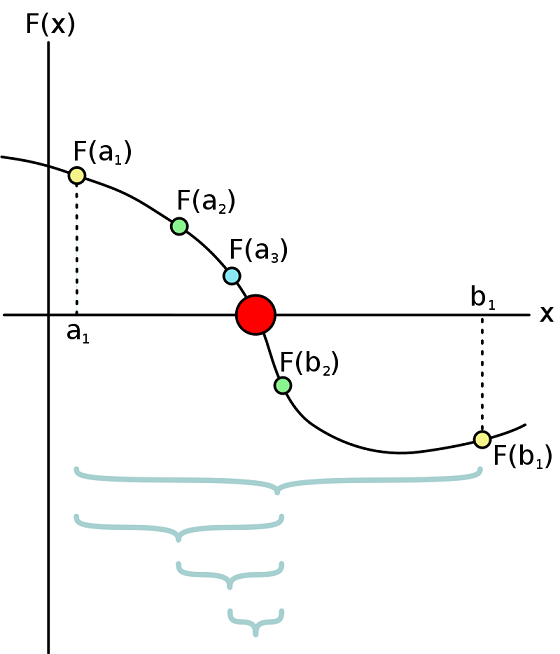
O método da bissecção é um método de busca de raízes que divide repetidamente um intervalo da função e então seleciona um subintervalo contendo a raiz para processamento adicional. Escolhe-se dois pontos extremos, a e b, de preferência para os quais haja um inversão de polaridade da curva.
é usado frequentemente para obter uma primeira aproximação de uma solução, a qual é então utilizada como ponto inicial para métodos que convergem mais rapidamente.
Trata-se de um método simples e robusto, relativamente lento quando comparado a métodos como o método de Newton ou o método das secantes.
PSEUDOCÓDIGO:
ENTRADA: Função f,
extremos do intervalo a, b,
tolerância TOL,
número máximo de iterações NMAX
CONDIÇÕES: a < b, ou f(a) < 0 e f(b) > 0 ou f(a) > 0 e f(b) < 0
SAÍDA: valor que difere de uma raiz de f(x)=0 por menos do que TOL
N ← 1
Enquanto N ≤ NMAX # limita o número de iterações para prevenir um loop infinito
c ← (a + b)/2 # novo ponto médio
Se f(c) = 0 or (b – a)/2 < TOL então # solução encontrada
Retorne(c)
Pare
Fim
N ← N + 1 # incrementa o contador de iterações
Se sinal(f(c)) = sinal(f(a)) então a ← c senão b ← c # novo intervalo
Fim
Retorne("O algoritmo falhou.") # núm. máximo de iterações excedido
Exemplo:
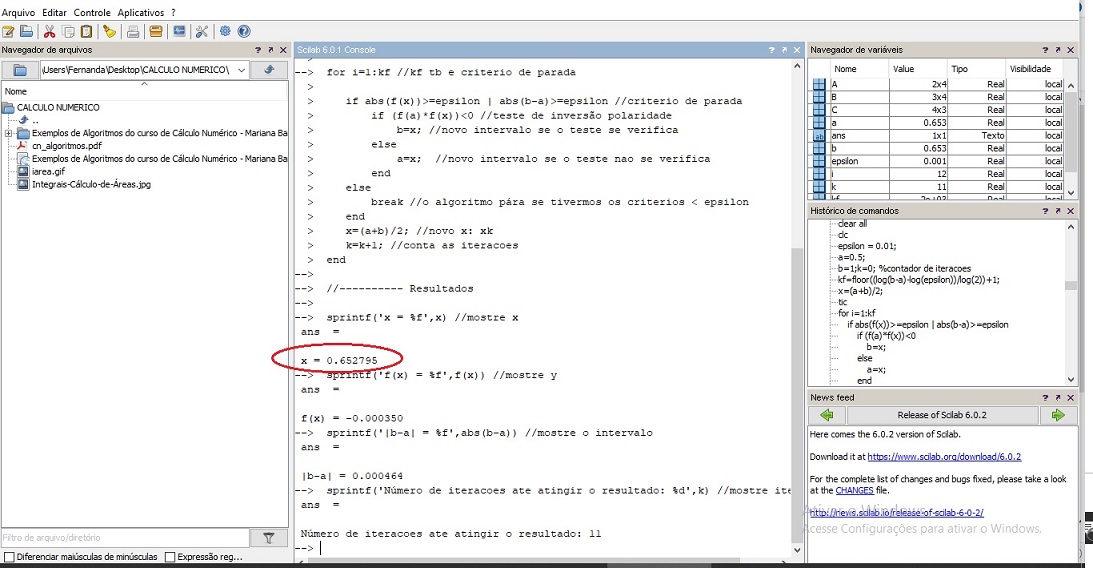
Para exemplificar, vamos aplicar o método da Bissecção à determinação da raiz da função f(x) = x² + ln x, no aplicativo Scilab, utilizando Scilab (~Matlab) script:
function f=f(x)
f= x*x + log(x); //log() é log natural no Scilab
end
clear all
clc
// ---------Parametros
epsilon = 0.001; //tolerancia
a=0.05; //limite superior do intervalo inicial
b=1; //limite inferior do intervalo inicial
k=0; //contador de iteracoes
kf = 2000 //no maximo de iterações
x=(a+b)/2; //x0 - intervalo inicial, onde (f(a)*f(x))<0
//-----------Iteracoes
for i=1:kf //kf tb e criterio de parada
if abs(f(x))>=epsilon | abs(b-a)>=epsilon //criterio de parada
if (f(a)*f(x))<0 //teste de inversão polaridade
b=x; //novo intervalo se o teste se verifica
else
a=x; //novo intervalo se o teste nao se verifica
end
else
break //o algoritmo pára se tivermos os criterios < epsilon
end
x=(a+b)/2; //novo x: xk
k=k+1; //conta as iteracoes
end
//---------- Resultados
sprintf('x = %f',x) //mostre x
sprintf('f(x) = %f',f(x)) //mostre y
sprintf('|b-a| = %f',abs(b-a)) //mostre o intervalo
sprintf('Número de iteracoes ate atingir o resultado: %d',k) //mostre iteracoes
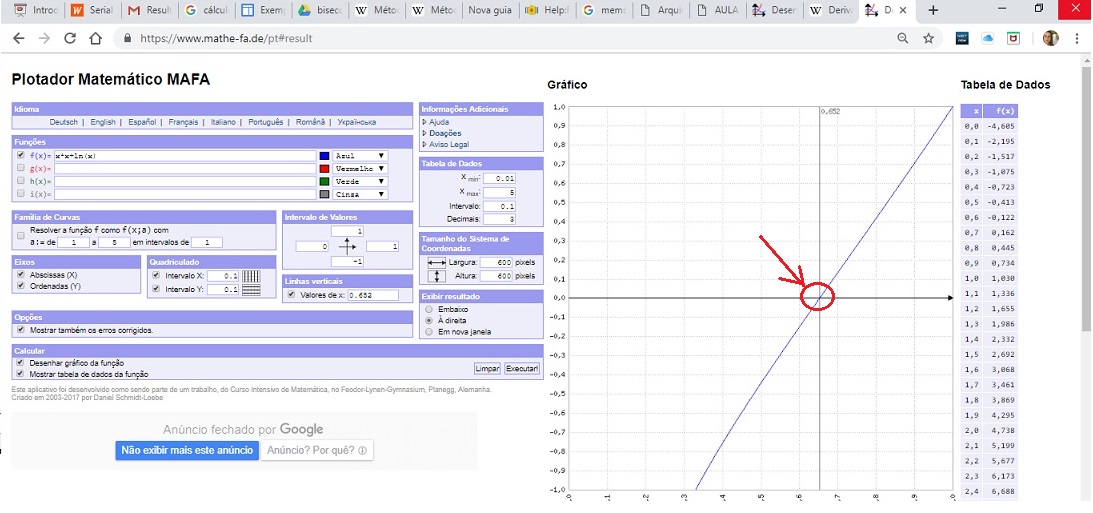
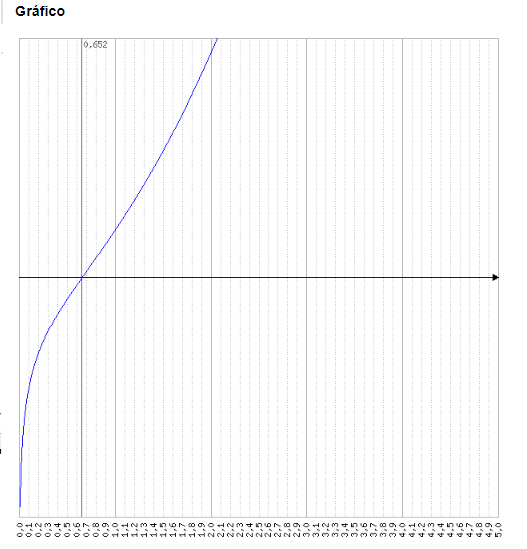
Gráfico: Plotador Matemático MAFA f(x) = x*x + lg(x)
Algoritmo Newton-Raphson
O Algoritmo ou método desenvolvido por Isaac Newton e Joseph Raphson, também tem o objetivo de estimar as raízes de uma função, com a diferença que converge muito mais rapidamente que o método da Bissecção.
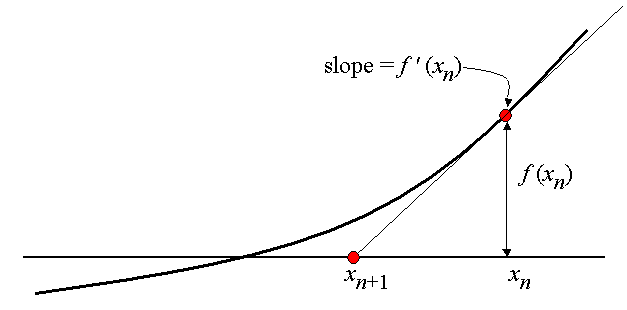
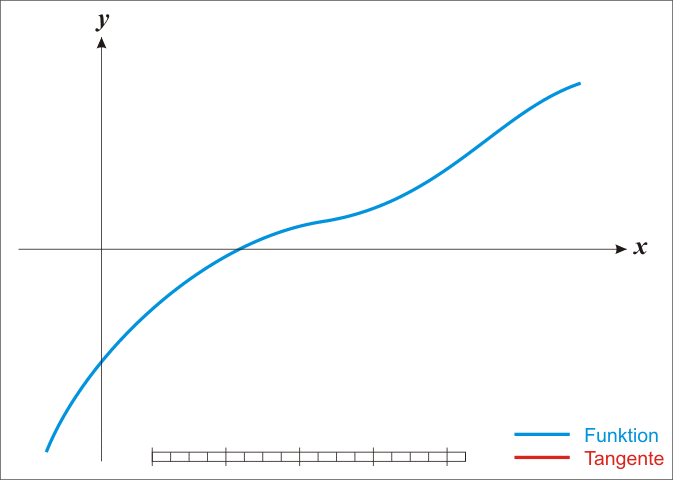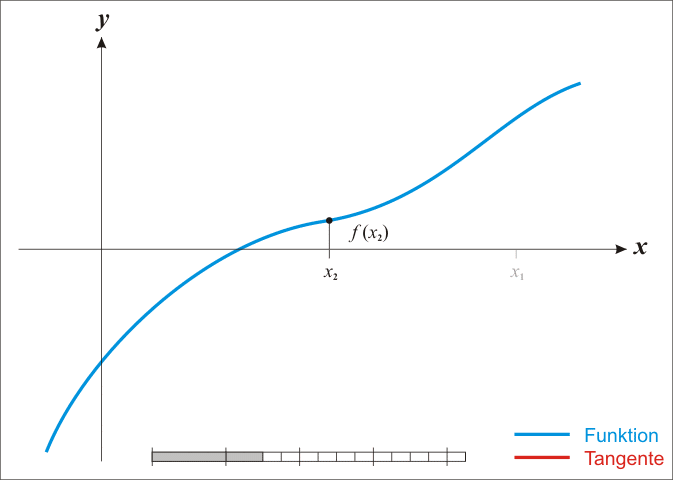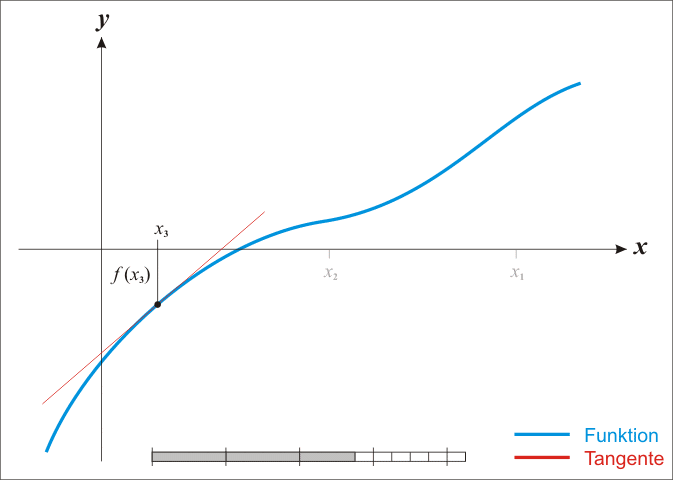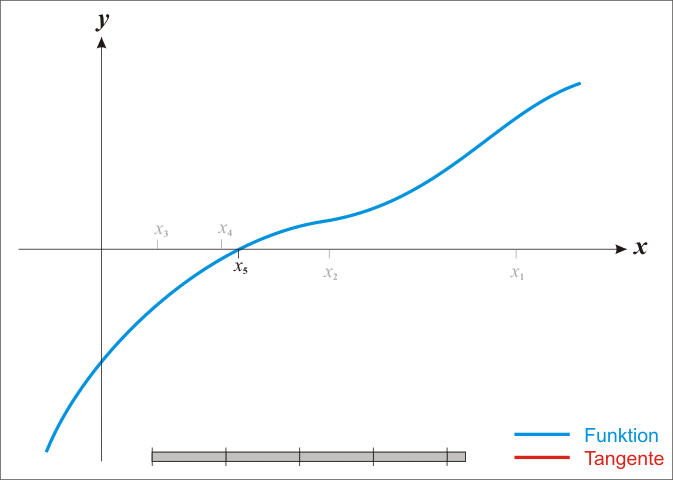
Após a escolha do valor inicial de aproximação do zero, calcula-se a equação da reta tangente (por meio da derivada) da função nesse ponto e a interseção dela com o eixo das abcissas, isto é, o zero desta reta (vide figura abaixo).
Pode ser provado que este segundo ponto estará muito mais próximo do zero da curva, do que o simples cálculo de ponto médio.
Repetindo-se o processo, cria-se um método iterativo para encontrarmos a raiz da função.
Em notação matemática, o método de Newton é dado pela seguinte sequência recursiva:
Exemplo:
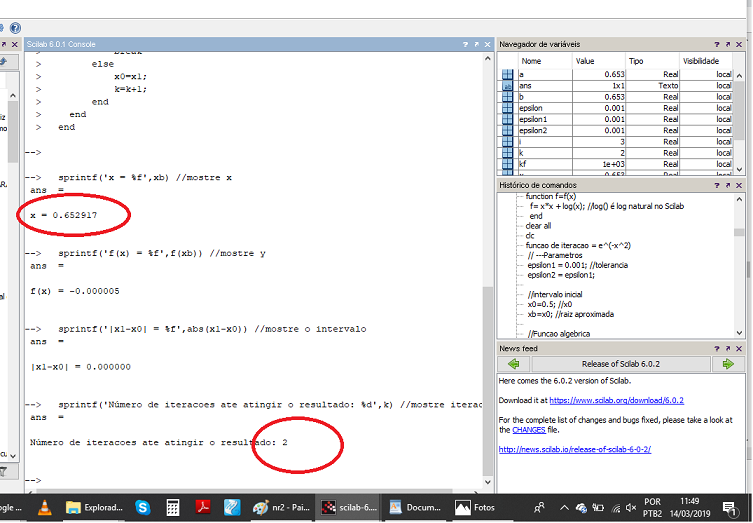
Algoritmo de Newton-Raphson aplicado ao cálculo das raízes da função f(x) = x² + log(x):
function f=f(x)
f= x*x + log(x); //log() é log natural no Scilab
end
//Funcao derivada
function fd=fd(x)
fd= 2*x + 1/x; //derivada
end
clear all
clc
funcao de iteracao = e^(-x^2)
// ---Parametros
epsilon1 = 0.001; //tolerancia
epsilon2 = epsilon1;
//intervalo inicial
x0=0.5; //x0
xb=x0; //raiz aproximada
k=0; //contador de iteracoes
kf=1000;//n° max de iteracoes
for i=1:kf //kf tb e criterio de parada
if (abs(f(x0))<epsilon1)
xb=x0;
break
else
x1=x0-(f(x0)/fd(x0));
if (abs(f(x1))<epsilon1 & abs(x1-x0)<epsilon2)
xb=x1
break
else
x0=x1;
k=k+1;
end
end
end
sprintf('x = %f',xb) //mostre x
sprintf('f(x) = %f',f(xb)) //mostre y
sprintf('|x1-x0| = %f',abs(x1-x0)) //mostre o intervalo
sprintf('Número de iteracoes ate atingir o resultado: %d',k) //mostre iteracoes
Inversão de Matrizes
Para solução de sistemas de Equações Lineares
Em inúmeras aplicações de Engenharia, a solução se resume a encontrar as raízes de um conjunto de n equações de primeiro grau, com n variáveis/incógnitas cada uma.
Os sistemas devem ter, no mínimo, uma equação para cada incógnita/variável, do tipo:
a.x + b.y + c.z = d e.x + f.y + g.z = h p.x + q.y + r.z = s
ou
[a b c ] [x] [d] [e f g ] . [y] = [h] [p q r ] [z] [s]
Se chamarmos de A, a matriz de coeficientes, K, à matriz de variáveis e B, à matriz de respostas:
A. K = B
A solução será dada por:
K = B/A = B. A-¹
Portanto, bastará multiplicar a matriz B pela inversa da matriz A.
Inverter matrizes, porém, em computador, não pode ser feito como um humano faz. Aprendemos na escola a inverter matrizes com métodos como o do Escalonamento, ou o de Cramer, que é extremamente ineficiente computacionalmente.
Existem métodos diretos e métodos iterativos de resolução de sistemas de equação.
Dos métodos diretos, destaca-se a Eliminação Gaussiana. Com relação aos métodos iterativos, destaca-se o de Gauss-Seidel.
Exemplo 1:
Resolução de sistema pela Regra de Cramer:
Exemplo 2:
Resolução do mesmo sistema por inversão da matriz no Scilab:
Algoritmo FFT
O Algoritmo da Transformada Rápida de Fourier (Fast Fourier Transform) permite o cálculo discreto e eficiente, computacionalmente, de transformada de fourier de sinais.