AULA 8 - Eletrônica Digital 1 - Graduação

Forma Canônica

Toda expressão booleana pode ser escrita em uma forma padronizada, denominada forma normal ou forma canônica �Duas formas normais são � Forma Normal Conjuntiva (FNC), Produto de Somas ou Produto de Maxtermos � Forma Normal Disjuntiva (FND), Soma de Produtos ou Soma de Mintermos

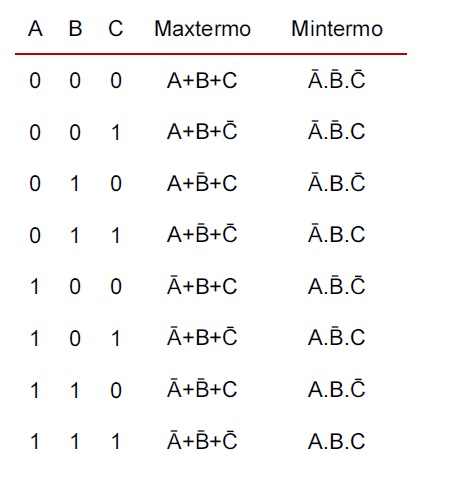
Maxtermos (ou maxitermos) � Variável com valor 0 é deixada intacta � Variável com valor 1 é alterada pela sua negação � Variáveis de uma mesma linha são conectadas por + (adição) � Mintermos (ou minitermos) � Variável com valor 1 é deixada intacta � Variável com valor 0 é alterada pela sua negação � Variáveis de uma mesma linha são conectadas por . (multiplicação)

Forma Normal Disjuntiva (FND)

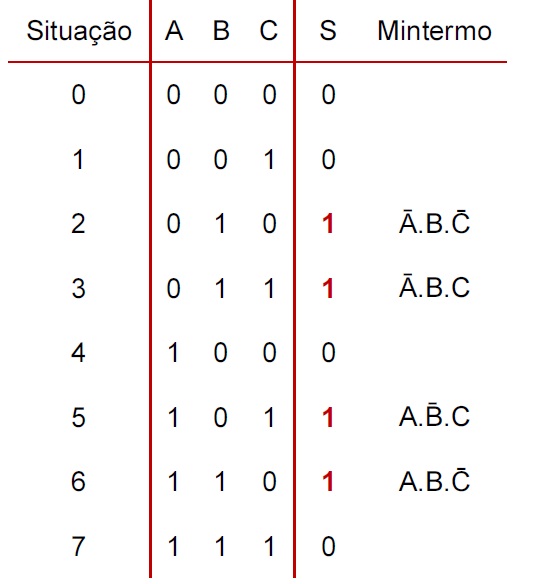
Mintermo (ou minitermo) é o termo produto associado à cada linha da tabela verdade, no qual todas as variáveis de entrada estão presentes � Dado um dado mintermo, se substituirmos os valores das variáveis associadas, obteremos 1 � Porém, se substituirmos nesse mesmo mintermo quaisquer outras combinações de valores, obteremos 0 � Dessa forma, se quisermos encontrar a equação para uma função a partir de sua tabela verdade, basta montarmos um OU entre os mintermos associados aos 1s da função

S é uma função das variáveis de entrada A, B e C � Os valores de (A,B,C) para os quais S=1 encontram-se nas situações 2, 3, 5 e 6 � Os mintermos associados a essas condições (ou seja, os mintermos 1) são mostrados na tabela ao lado � Logo, a expressão em soma de produtos (FND) para S será o OU entre estes produtos � S = Ā.B.C + Ā.B.C + A.B.C + A.B.C

Forma Normal Conjuntiva (FNC)

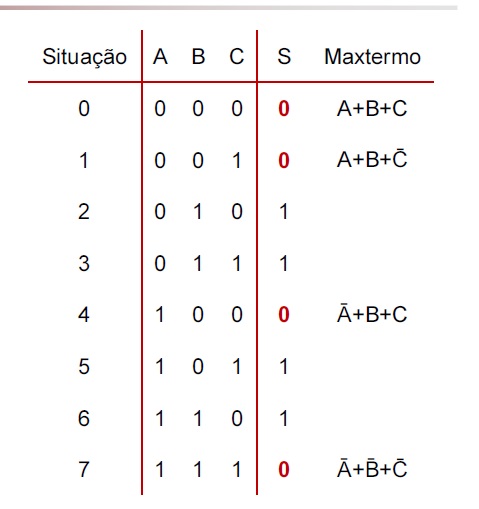
Maxtermo (ou maxitermo) é o termo soma associado à cada linha da tabela verdade, no qual todas as variáveis de entrada estão presentes � Dado um dado maxtermo, se substituirmos os valores das variáveis associadas, obteremos 0 � Porém, se substituirmos nesse mesmo maxtermo quaisquer outras combinações de valores, obteremos 1 � Dessa forma, se quisermos encontrar a equação para uma função a partir de sua tabela verdade, basta montarmos um E entre os maxtermos associados aos 0s da função

S é uma função das variáveis de entrada A, B e C � Os valores de (A,B,C) para os quais S=0 encontram-se nas situações 0, 1, 4 e 7 � Os maxtermos associados a essas condições (ou seja, os maxtermos 0) são mostrados na tabela ao lado � Logo, a expressão em produto de somas (FNC) para S será o E entre estas somas � S = (A+B+C) . (A+B+C). (Ā+B+C) . (Ā+B+C)

Uma vez obtida a forma normal de uma função booleana, é possível simplificá-la por meio de manipulação algébrica, respeitando os postulados e propriedades da álgebra booleana, com visto anteriormente.

Alternativamente ao método de simplificação algébrico por fatoração, há outro método de simplificação baseado na identificação visual de grupos de mintermos que podem ser simplificados � Para tanto, é necessário que os mintermos sejam dispostos de maneira conveniente, em tabelas conhecidas como diagramas ou mapas de Veitch-Karnaugh.