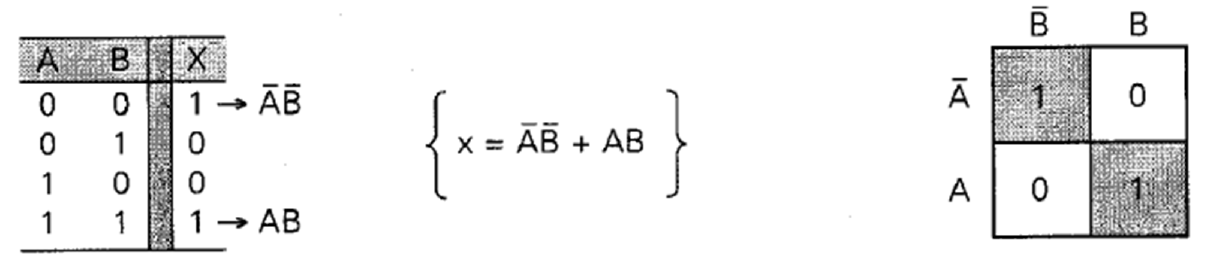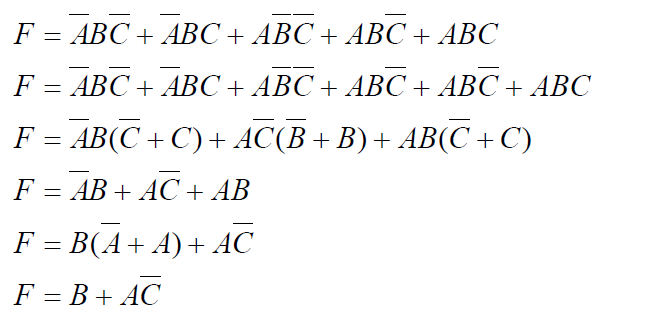AULA 8 - Eletrônica Digital 1 - Graduação
Os circuitos lógicos podem ser representados por funções booleanas, ou seja, admite-se que todos os circuitos lógicos estabeleçam as relações entre entradas e saída, obedecendo à função booleana que os representa.
Quando necessário, é possível obter a função booleana por meio da tabela verdade do circuito.
A seguir, são descritas as relações entre as formas de representação de um circuito lógico.
Forma Canônica
Toda expressão booleana pode ser escrita em uma forma padronizada, denominada forma normal ou forma canônica.
Duas formas normais são:
- Forma Normal Conjuntiva (FNC), Produto de Somas ou Produto de Maxtermos
- Forma Normal Disjuntiva (FND), Soma de Produtos ou Soma de Mintermos
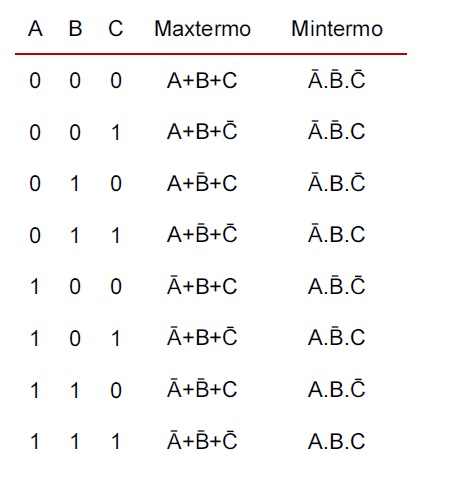
Maxtermos (ou maxitermos)
As regras para compor as expressões são:
- Variável com valor 0 é deixada intacta.
- Variável com valor 1 é descrita pela sua negação.
- Variáveis de uma mesma linha são conectadas por + (adição)
Mintermos (ou minitermos)
As regras para compor as expressões são:
- Variável com valor 1 é deixada intacta.
- Variável com valor 0 é descrita pela sua negação.
- Variáveis de uma mesma linha são conectadas por . (multiplicação)
Forma Normal Disjuntiva (FND)
Mintermo (ou minitermo) é o termo produto associado à cada linha da tabela verdade, no qual todas as variáveis de entrada estão presentes.
Dado um dado mintermo, se substituirmos os valores das variáveis associadas, obteremos 1.
Porém, se substituirmos nesse mesmo mintermo quaisquer outras combinações de valores, obteremos 0.
Dessa forma, se quisermos encontrar a equação para uma função a partir de sua tabela verdade, basta montarmos um OU entre os mintermos associados aos 1s da função.
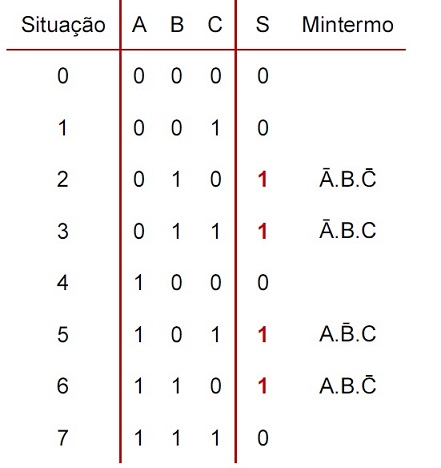
- S é uma função das variáveis de entrada A, B e C
- Os valores de (A,B,C) para os quais S=1 encontram-se nas situações 2, 3, 5 e 6
- Os mintermos associados a essas condições (ou seja, os mintermos 1) são mostrados na tabela abaixo:
Logo, a expressão em soma de produtos (FND) para S será o OU entre estes produtos:
- S = Ā.B.C + Ā.B.C + A.B.C + A.B.C
Forma Normal Conjuntiva (FNC)
Maxtermo (ou maxitermo) é o termo soma associado à cada linha da tabela verdade, no qual todas as variáveis de entrada estão presentes.
Dado um dado maxtermo, se substituirmos os valores das variáveis associadas, obteremos 0.
Porém, se substituirmos nesse mesmo maxtermo quaisquer outras combinações de valores, obteremos 1.
Dessa forma, se quisermos encontrar a equação para uma função a partir de sua tabela verdade, basta montarmos um E entre os maxtermos associados aos 0s da função:
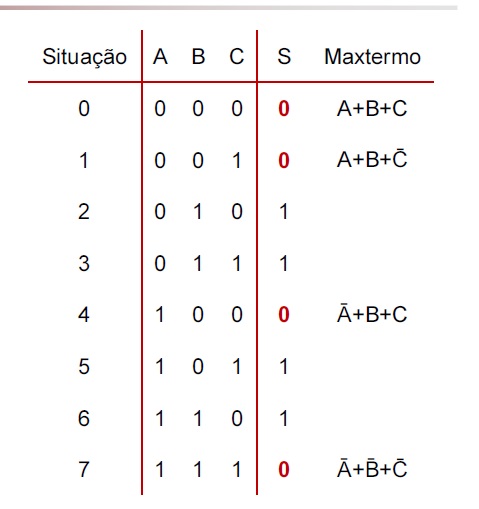
- S é uma função das variáveis de entrada A, B e C
- Os valores de (A,B,C) para os quais S=0 encontram-se nas situações 0, 1, 4 e 7
- Os maxtermos associados a essas condições (ou seja, os maxtermos 0) são mostrados na tabela abaixo:
Logo, a expressão em produto de somas (FNC) para S será o E entre estas somas:
- S = (A+B+C) . (A+B+C). (Ā+B+C) . (Ā+B+C)
Uma vez obtida a forma normal de uma função booleana, é possível simplificá-la por meio de manipulação algébrica, respeitando os postulados e propriedades da álgebra booleana, com visto anteriormente.
Alternativamente ao método de simplificação algébrico por fatoração, há outro método de simplificação baseado na identificação visual de grupos de mintermos que podem ser simplificados.
Para tanto, é necessário que os mintermos sejam dispostos de maneira conveniente, em tabelas conhecidas como diagramas ou mapas de Veitch-Karnaugh.
Mapas de Karnaugh
Método gráfico usado para simplificar uma equação lógica ou converter uma tabela verdade no seu circuito lógico correspondente.
O mapa (ou diagrama) de Karnaugh é uma forma ordenada utilizada para minimizar uma expressão lógica, que geralmente produz um circuito com configuração mínima.
É construído com base na tabela verdade e pode ser facilmente aplicado em funções envolvendo duas a seis variáveis.
Acima disso, os mapas se tornam muito complicados, sendo melhor fazer a análise por meio de programas de computador.
No caso de sete ou mais variáveis, o método torna-se complicado e devemos usar técnicas mais elaboradas. Representa-se o mapa de Karnaugh por uma tabela em forma de linhas e colunas.
Essa tabela, de acordo com o número de variáveis, é dividida em células obedecendo à proporção 2n, em que n é o número de variáveis de entrada envolvidas.
Obtenção e Simplificação de expressões por Mapas de Karnaugh
Baseia-se no fato de que X + X' = 1
Exemplo:
S = ABC + ABC' = AB(C+C') = AB.1 = AB
A entrada C torna-se irrelevante para a saída S.
Obtenção da Expressão
- Unir blocos de 1´s adjacentes
- Deve-se buscar a formação de blocos com a maior quantidade possível de 1´s -> respeitada a regra de N = 2n -> N = quantidade de 1´s no bloco → Formação de pares, quadras, oitavas,...
- Expressão final = “soma” das expressões de cada bloco
- Usar o menor número de blocos possível;
- Na expressão de cada bloco, eliminam-se as variáveis que mudam de estado dentro do bloco (X' → X ou X → X');
- As variáveis que não mudam de estado são mantidas na expressão, representando o seu respectivo valor fixo no bloco:
A = 1 → A e A = 0 → A' - Em cada bloco, pelo menos um dos 1's deve ser exclusivo àquele grupo (senão implica em redundância);
- Quanto maior o bloco, maior o número de variáveis eliminadas e mais simplificada fica a expressão final:
- Unidade: nenhuma variável eliminada;
- Par: uma variável eliminada;
- Quadra: duas variáveis eliminadas;
- Oitava: três variáveis eliminadas;
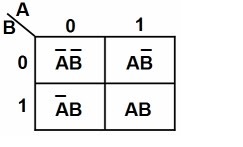
Mapa para duas variáveis de entrada
Quando utilizada duas variáveis, o mapa de Karnaugh apresenta a seguinte configuração, onde cada espaço será completado com seu nível lógico equivalente.
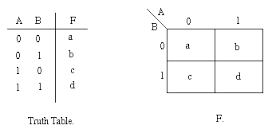
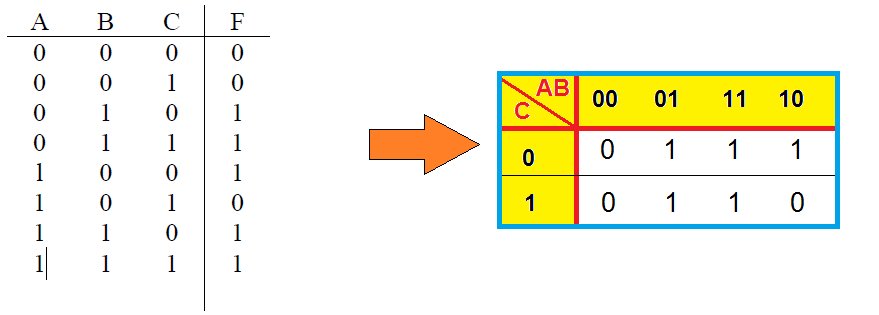
Exemplo, seja a tabela-verdade com entradas A e B e saída F:
Utiliza-se a seguinte tabela-verdade para montar o mapa de Karnaugh, onde A e B são as entradas e F a saída:
A B F
0 0 S0=1
0 1 S1=0
1 0 S2=1
1 1 S3=1
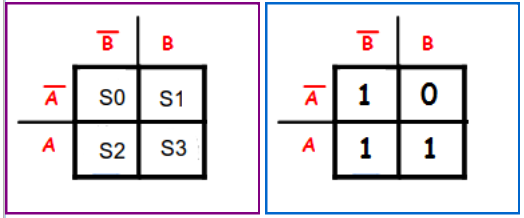
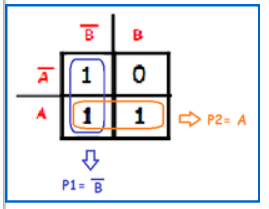
As saídas da TV colocadas no MK seriam:
Com o mapa já construído, deve-se diferenciar os minitermos, ou seja, considerar somente os campos que possuem 1 como solução final.
Eles devem ser agrupados em pares, para isso ocorrer os elementos tem que estar lado-a-lado, pode ser tanto na horizontal como na vertical.
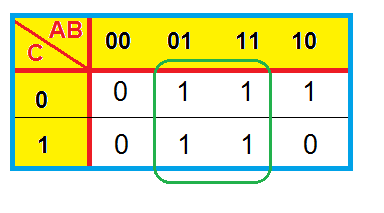
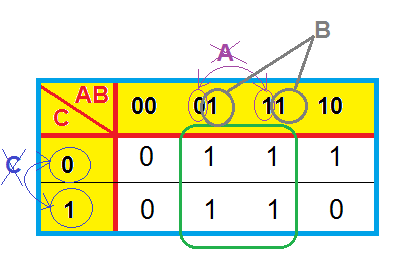
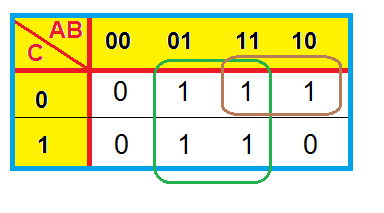
Separando em pares, obtem-se:
Os campos selecionados com a cor azul, estão respectivamente na coluna B'.
Já os campos selecionados com a cor laranja estão na linha A.
Formando assim a expressão simplificada:
F = B' + A
Observe a posição fixa dos bits, referentes aos minitermos:
Neste exemplo, não foi possível criar pares/grupos para minimizar a expressão de saída:
Mapa para três variáveis de entrada
O mapa de 3 Variáveis vai ter 8 posições de minitermos (m0 a m7) e o objetivo é formar blocos de 2 ou 4 1's, afim de minimizar a expressão de saída.
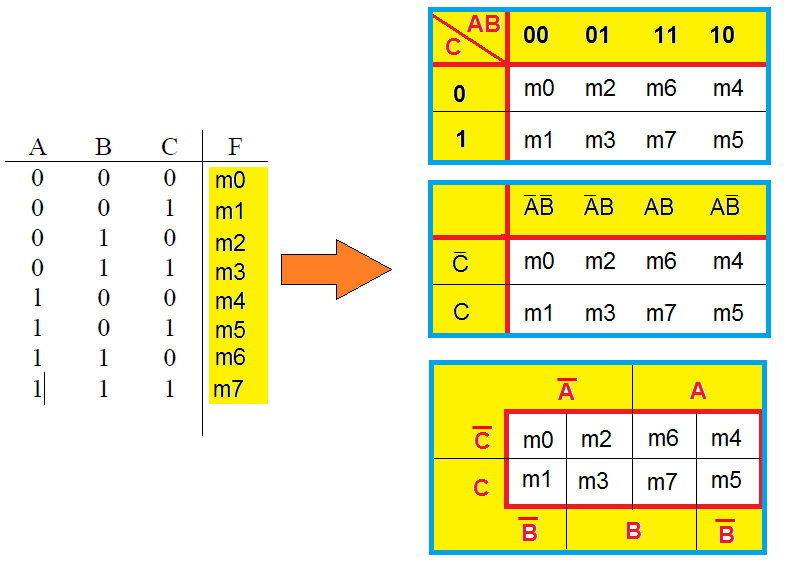
São encontradas várias formas de se representar o MK de 3 variáveis na bibliografia, conforme a figura abaixo:
Além das três formas acima ilustradas, por vezes o mapa é construído de forma transposta a estas.
O importante é que o aluno entenda que cada posição de minitermo refere-se aos respectivos valores das variáveis (barradas ou não), naquela posição horizontal e vertical da tabela.
Exemplo:
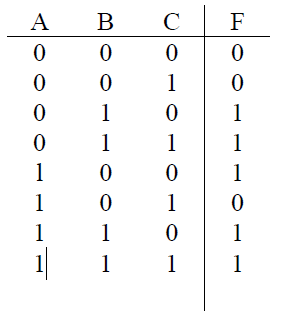
Minimize o circuito definido pela Tabela-Verdade abaixo:
Se fôssemos utilizar Lógica Booleana para realizar a minimização algébrica, o procedimento seria algo do tipo:
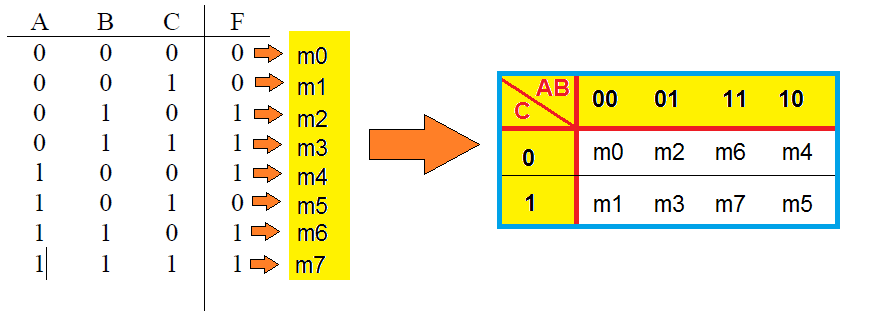
Por MK (Mapa de Karnaugh), o procedimento inicia-se pelo preenchimento do mapa, observando as posições dos minitermos:
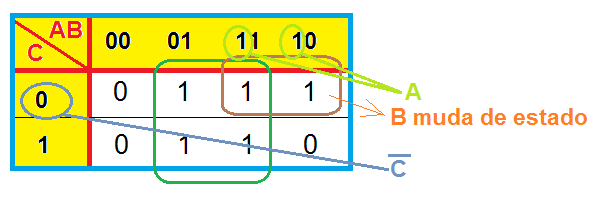
Fica claro o bloco quadrado de 4 1´s, no centro do mapa:
Neste bloco, as variáveis A e C mudam de estado e, portanto, são irrelevantes. A variável B entra com valor 1 (portanto, não barrada), na expressão final.
Como não há possibilidade de se fazer outro grupo de 4 minitermos, resta agrupar o 1 restante em um par, com seu 1 adjacente. Neste bloco, o A entra com valor 1, o B muda de estado e o C, com valor zero, reduzindo a expressão a AC' .
Em resumo, através de MK, o trabalho de minimização foi bastante resumido à uma análise gráfica simples, com relação à análise algébrica.
Obtém-se, novamente, que F = B + AC'
Mapa para quatro variáveis de entrada
O mapa de 4 Variáveis vai ter 16 posições de minitermos (m0 a m15) e o objetivo é formar blocos de 2, 4 ou 8 1's, afim de minimizar a expressão de saída.
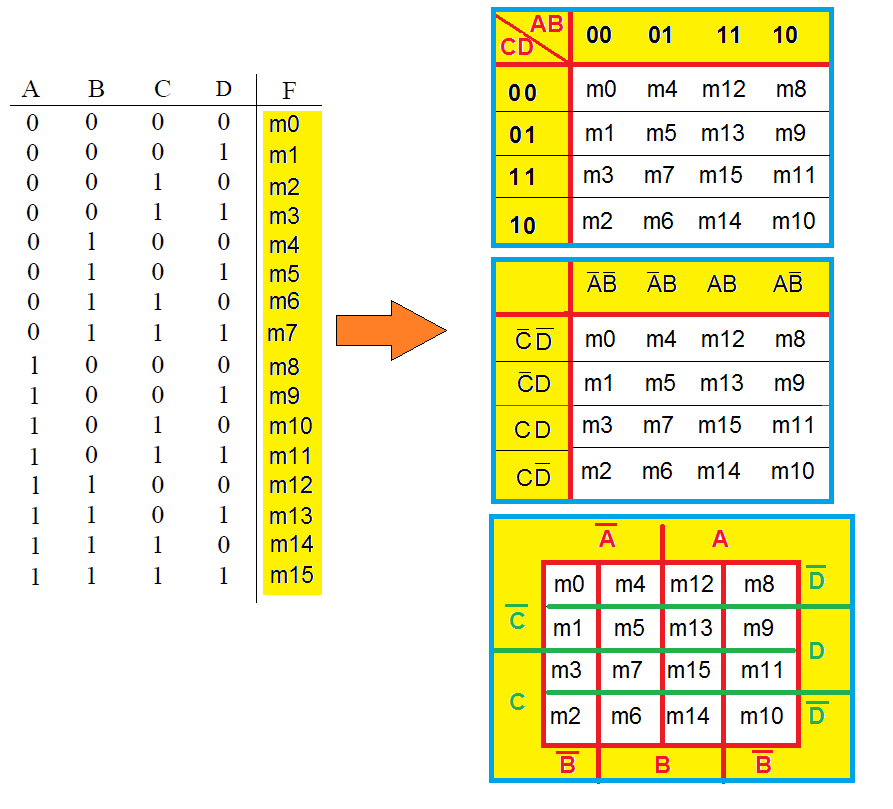
São encontradas várias formas de se representar o MK de 4 variáveis na bibliografia, conforme a figura abaixo:
Além das três formas acima ilustradas, por vezes o mapa é construído de forma transposta a estas.
O importante é que o aluno entenda que cada posição de minitermo refere-se aos respectivos valores das variáveis (barradas ou não), naquela posição horizontal e vertical da tabela.
Exemplo:
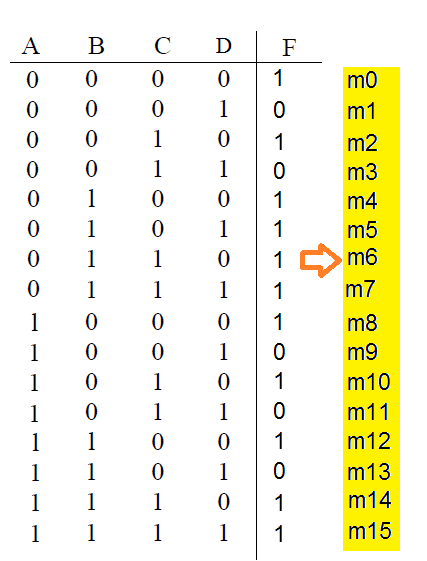
Minimize o circuito definido pela Tabela-Verdade abaixo:
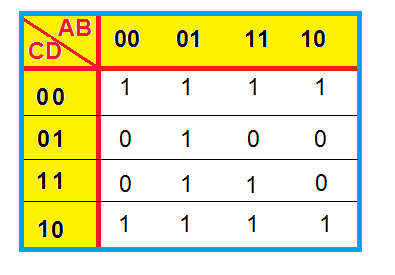
Transpondo da tabela para o diagrama temos:
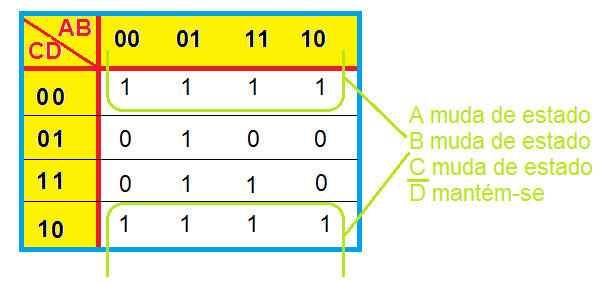
Podemos observar o bloco de 8 1´s, composto pela primeira e última linha do mapa:
Neste bloco, as variáveis A, B e C mudam de estado e, portanto, são irrelevantes. A variável D entra com valor 0 (portanto, barrada), na expressão final.
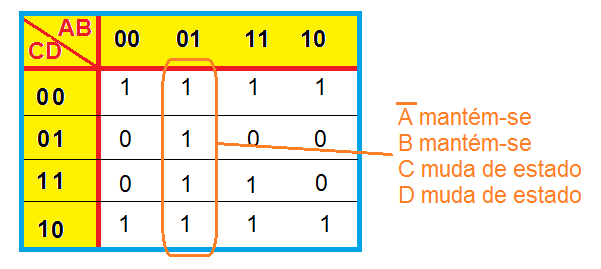
Na figura abaixo, destacamos a quadra vertical:
Neste bloco, C e D mudam de estado para os minitermos e nesta coluna, A entra barrado e B entra não-barrado.
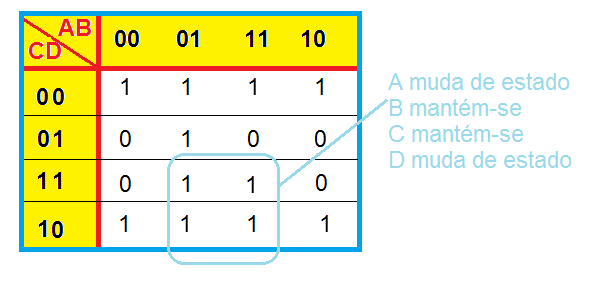
Por fim, na figura abaixo, destacamos a outra quadra, na qual A e D mudam de estado e B e C mantém-se.
Portanto, para esta TV, obtém-se que a saída simplificada por MK pode ser dada por: F = D' + A'.B + B.C .
Mapa para cinco ou mais variáveis de entrada
O mapa de 5 Variáveis vai ter 32 posições de minitermos (m0 a m31) e o objetivo é formar blocos de 2, 4, 8 ou 16 1's, afim de minimizar a expressão de saída.
Os mapas de 5 ou mais variáveis não são mais planares, então são descritos como duas tabelas "superpostas", ou entrelaçadas, e os grupos podem ser formados tridimensionalmente, entre ambas as tabelas.
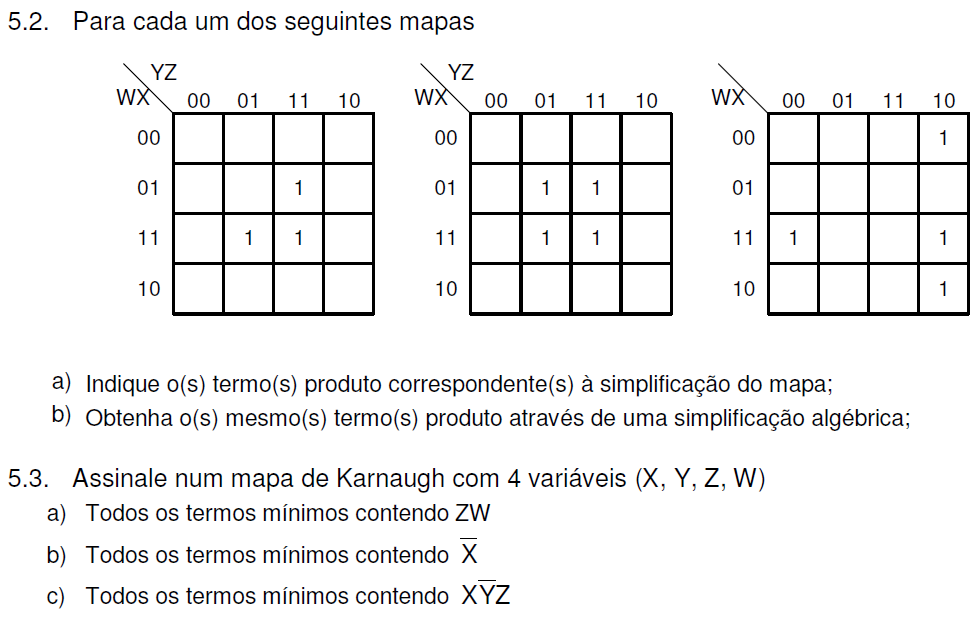
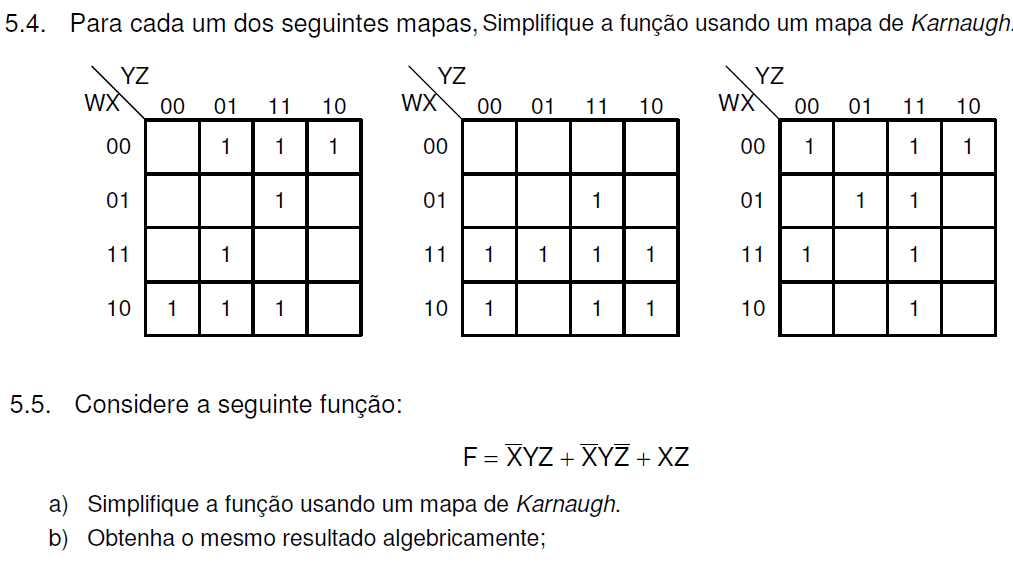
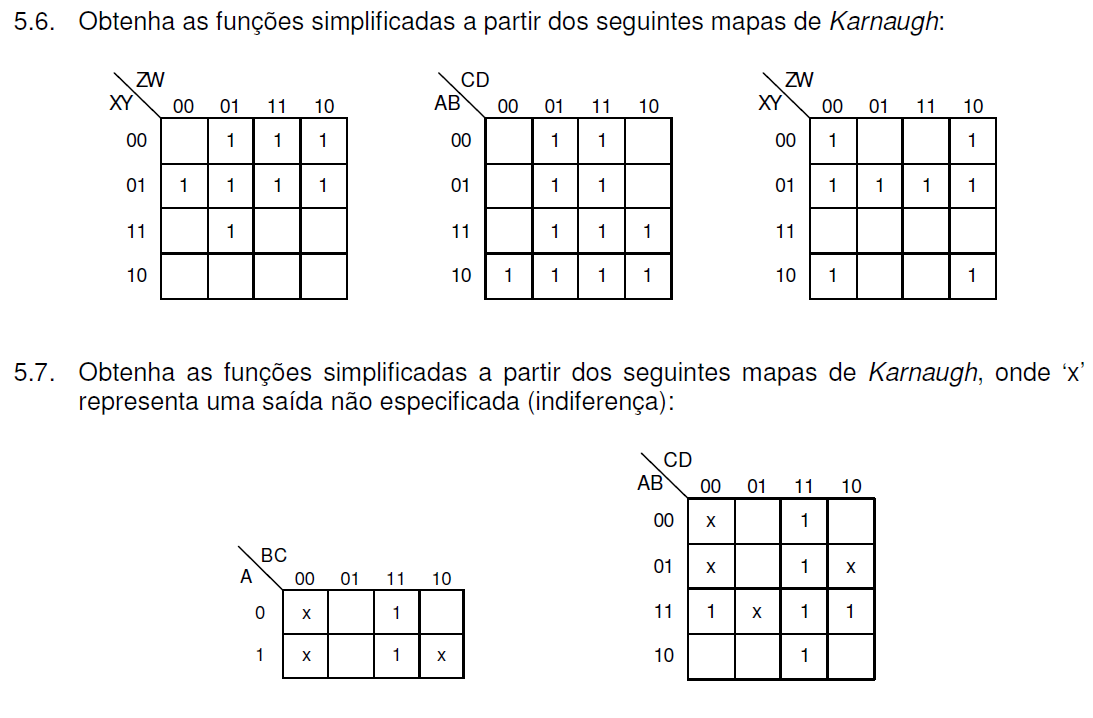
Exercício:
Condições irrelevantes
Condições irrelevantes, ou "don´t care"