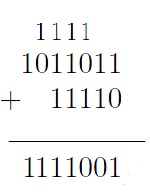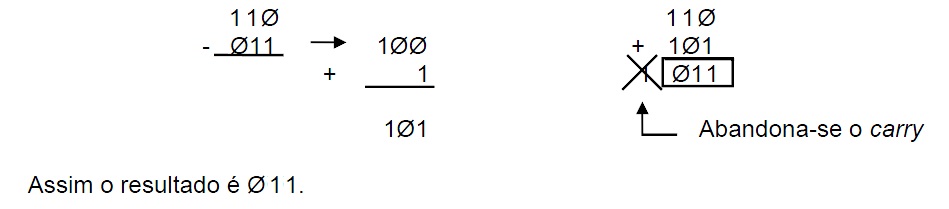AULA 13 - Eletrônica Digital 1 - Graduação
<<< Voltar para página principal do curso
Circuitos Aritmeticos
Como vimos anteriormente os circuitos combinacionais, vamos encontrar alguns circuitos importantes de grande utilidade e que sao a essencia da computacao hoje existente. Sao os circuitos aritmeticos tambem muito conhecidos como ULA (Unidade Logica Aritmetica).
Meio Somador
Como sabemos, os computadores trabalham na forma binaria e ja é de se esperar que o mesmo faca suas operacoes na forma binaria.
Relembrando a soma de dois numeros binarios teremos:
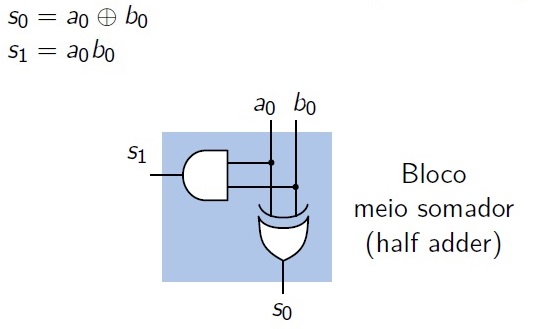
O diagrama de blocos seria uma porta XOR para a saída de soma S e uma porta AND para Ts, também chamada de carry (C).
Esse circuito é denominado Meio Somador (Half-Adder).
Somador Completo
O meio somador possibilita efetuar a soma de numeros binarios com 1 algarismo.
Mas no mundo real se faz necessario que esta soma seja efetuadas com um numero maior de algarismos.
Para satisfazer estas condicoes o circuito necessita de uma entrada de transporte proveniente de uma saida de transporte da casa binária anterior.
Para melhor compreensao, vamos analisar o caso da soma a seguir:
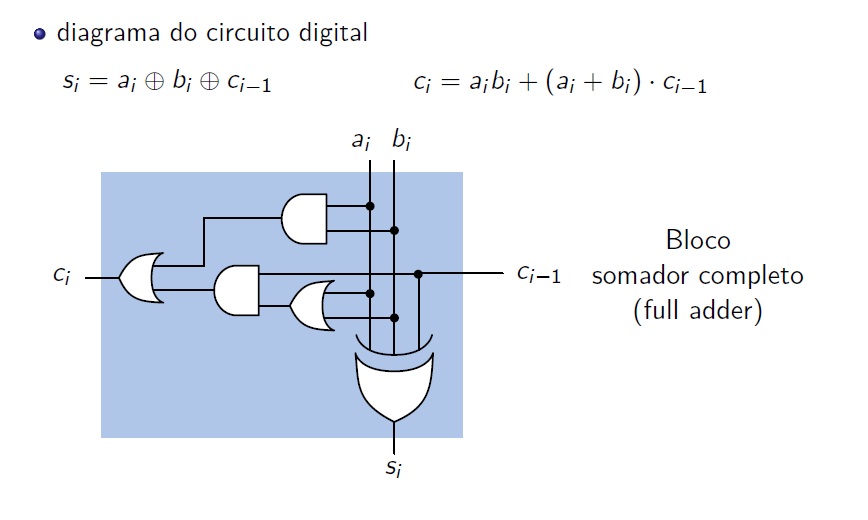
Extrapolando para a soma de duas palavras binárias A e B, de comprimentos (números de bits) quaisquer, i+1, onde ai e bi são os bits da casa binária i, a serem somados e ci é o bit de carry (ou transporte, ou vai-um) daquela casa binária:
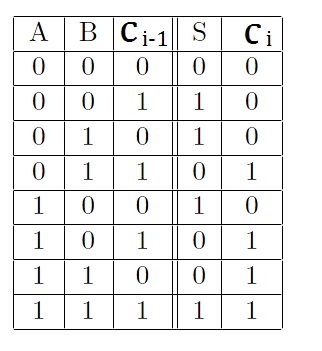
Desta forma a tabela verdade ficaria do seguinte modo:
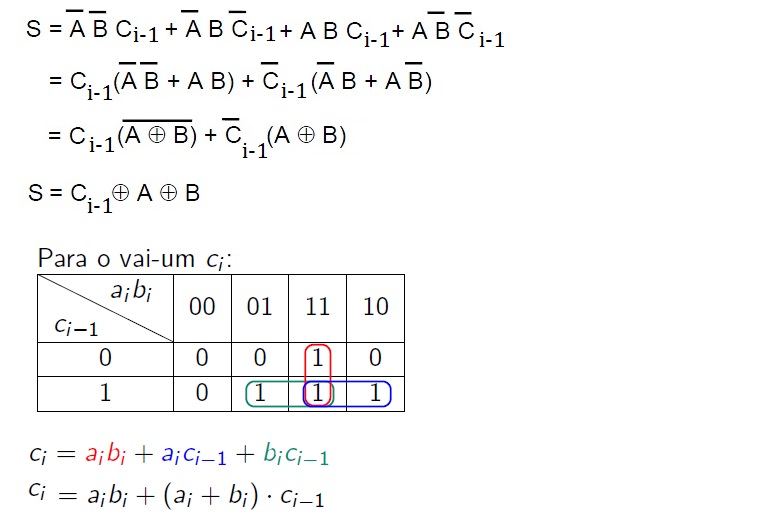
e o circuito completo, após minimização, seria:
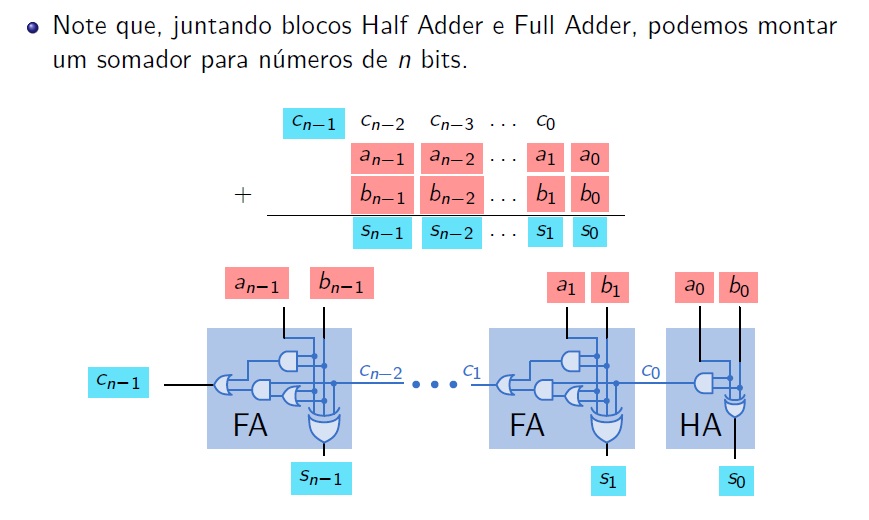
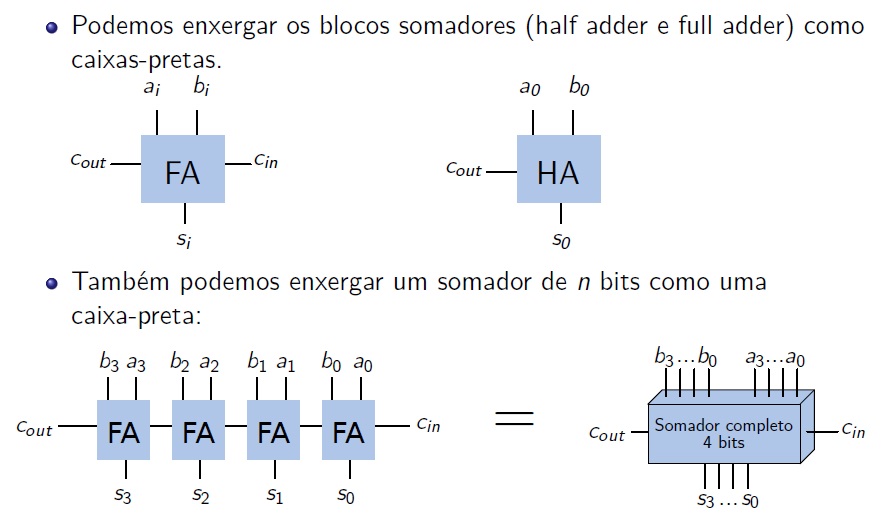
Assim, os somadores digitais são, na verdade, blocos modulares, caixas-pretas as quais, combinadas, permitem que se implemente circuitos somadores para tantos bits quantos forem necessários:
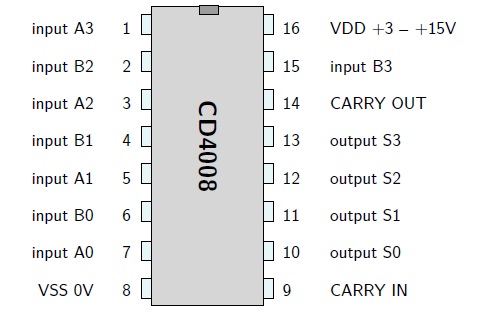
Exemplos de somadores comerciais: 7483 (TTL) e CD4008 (CMOS)
Subtração Binária
Grande parte dos sistemas digitais usa um único circuito para efetuar subtração e soma.
Neste circuito, a subtração é efetuada por soma, num processo conhecido como complemento de dois.
COMPLEMENTO DE UM NÚMERO BINÁRIO
O complemento de um número binário é obtido trocando-se todos "Øs" por "1s" e todos "1s" por "Øs".
Exemplo:
Obter o complemento do binário 1Ø1Ø11
Solução:
O complemento é Ø1Ø1ØØ
COMPLEMENTO DE DOIS DE UM NÚMERO BINÁRIO
O complemento de dois de um número binário é obtido tomando-se o complemento do número binário e somando-se 1 a este complemento.
Exemplo 1:
Obter o complemento de dois do binário correspondente ao decimal 3.
Solução:
3(10) = 11(2)
O complemento de 11 é ØØ. O complemento de dois de 11 é ØØ + 1 = Ø1
Então, o complemento de 2 de 11 é Ø1
Exemplo 2:
Obter o complemento de dois do binário Ø1.
Solução:
O complemento de Ø1 é 1Ø. O complemento de 2 de Ø1 é 1Ø + 1 = 11
Exemplo 3:
Efetuar a subtração através da soma 1Ø1 (Minuendo) - Ø11 (Subtraendo)
Solução:
Toma-se o complemento de dois do subtraendo e soma-se este complemento ao minuendo; tem-se então:
Para a subtração genérica de um número B menos o número A binário: