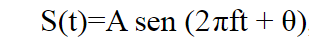AULA 1 - Circuitos 2 - Engenharia
<<< Voltar para página principal do curso
Circuitos em Corrente Alternada (C.A.)
No fim da década de 1880 viveu-se nos Estados Unidos da América um período conhecido como a Guerra das Correntes.
Nessa época já existia uma rede elétrica pública, usada principalmente para alimentar lâmpadas incandescentes e motores elétricos. A exploração dessa rede elétrica revertia em grandes benefícios para Thomas A. Edison, que tinha obtido várias patentes pela invenção da lâmpada e de vários dispositivos para gerar corrente contínua.
Outras pessoas tentaram entrar nesse novo negócio milionário com as suas inovações; e George Westinghouse, que já tinha tido sucesso comercial com as suas próprias patentes, contratou Nikola Tesla, um cientista brilhante, imigrante da Croácia.
Tesla obteve uma patente pelo dispositivo esquematizado acima, utilizado para produzir e distribuir corrente alternada.
A guerra das correntes acabaria por ser ganha pelo sistema de corrente alternada de Tesla e Westinghouse: uma das principais vantagens sobre o sistema de corrente contínua de Edison é a facilidade de poder aumentar ou diminuir a tensão por meio de transformadores.
fonte: Universidade do Porto
Funções Senoidais
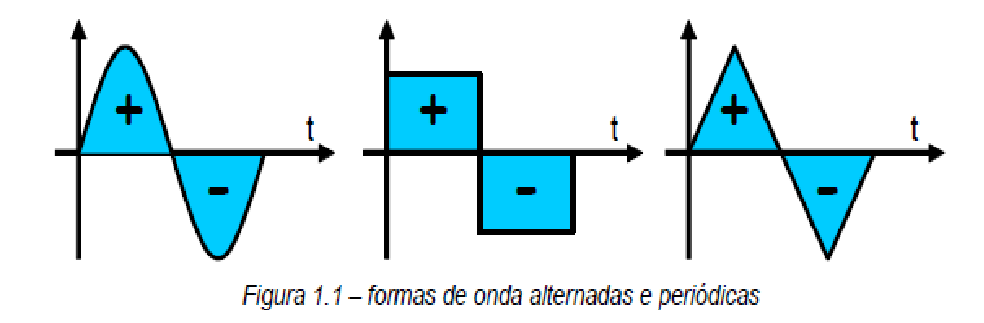
Sinais periódicos, ou alternados, são aqueles que completam um padrão de comportamento durante um período mensurável de tempo.
Em um sistema de corrente e tensão alternadas, estas grandezas invertem continuamente suas polaridades (sentido e intensidade).
Em particular, existem correntes e tensões do tipo senoidais, ou sinusoidais, as quais são alternadas e representadas por funções tipo seno/cosseno.
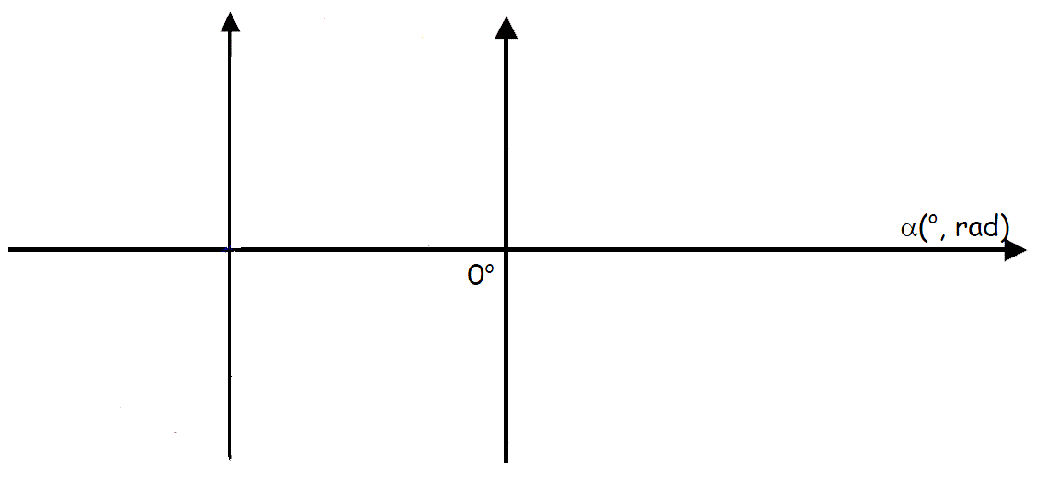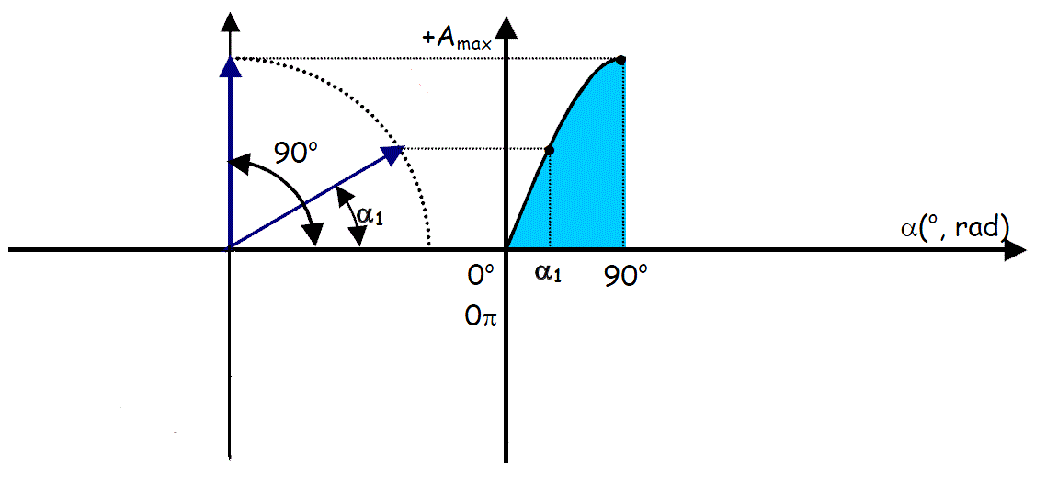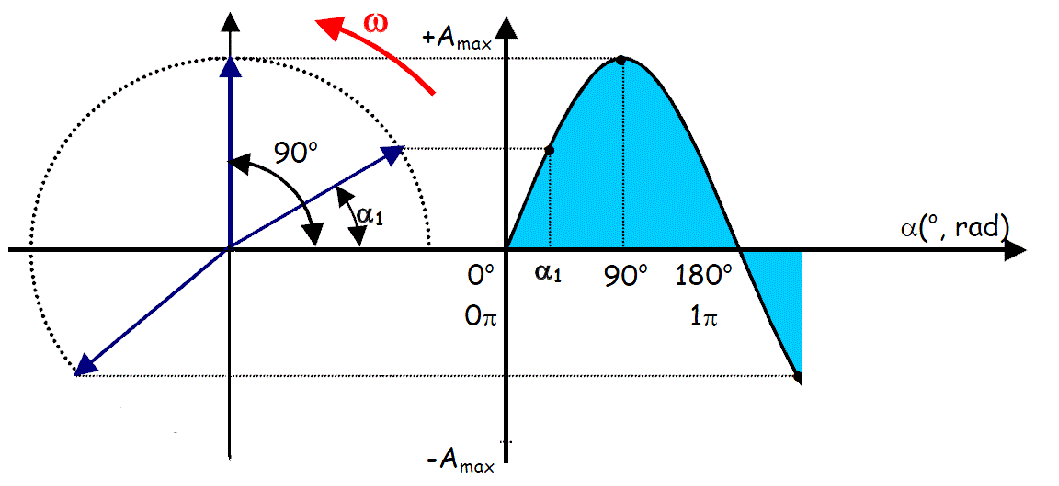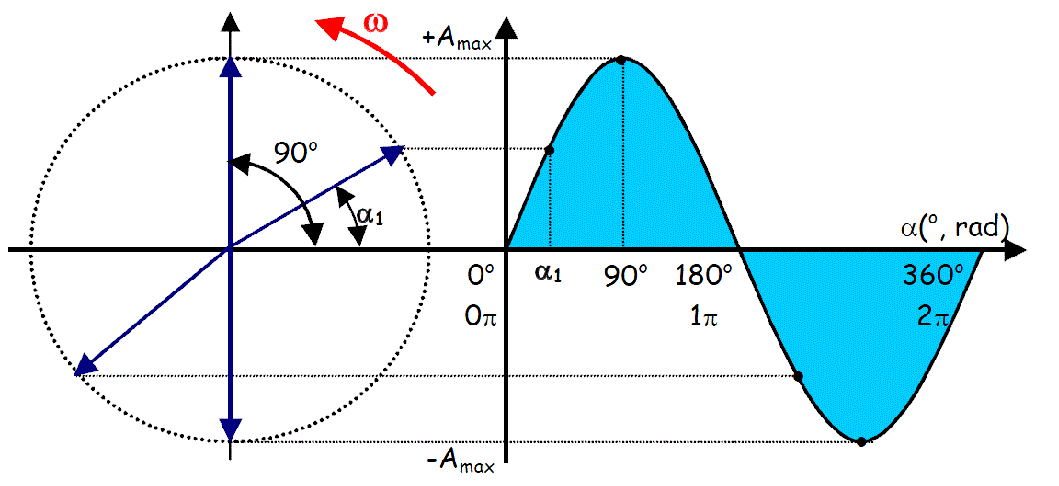
Uma função sinusoidal é uma função alternada da forma:
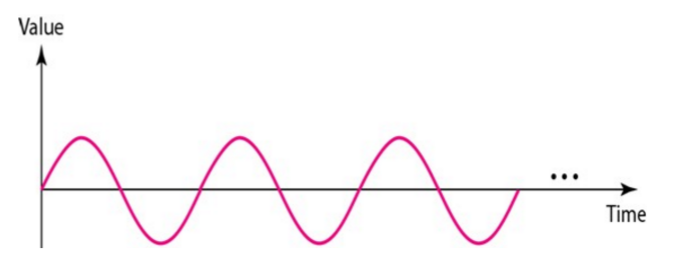
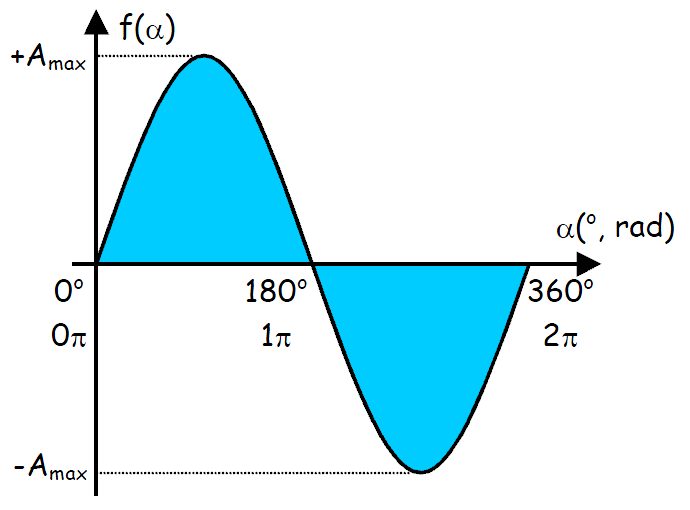
que oscila entre dois valores +A (máximo ou "de pico) e -A e tem a mesma forma da função seno ou cosseno, como mostra a figura abaixo.
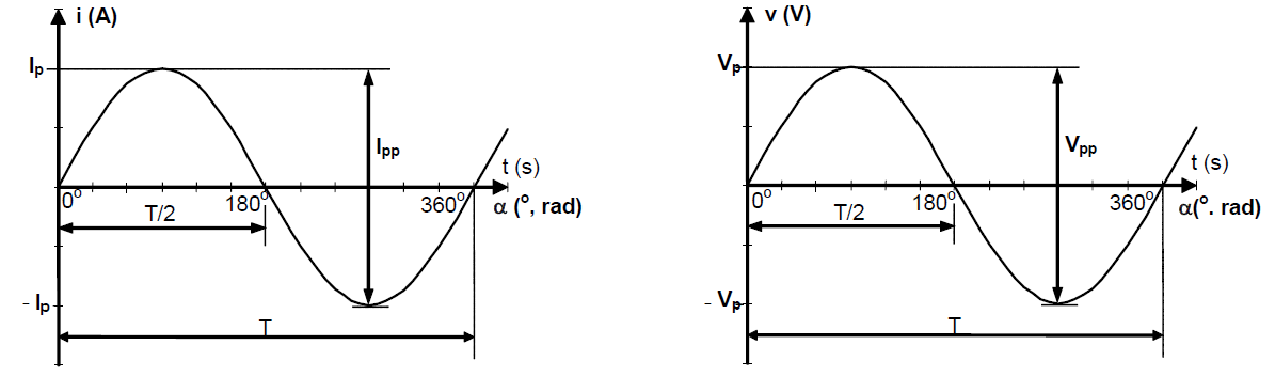
É necessário conhecer os valores das 3 distâncias Ip/Vp (valor de pico), T (período) e θ (fase), para caracterizar cada uma dessas funções.
Mas, porque Corrente Alternada (C.A.)?
- Facilidade na geração e transformação;
- Motores CA são mais baratos que motores CC;
- Teoremas de análise de Circuitos CC podem ser aplicados a circuitos CA alimentados por sinais senoidais;
- Qualquer sinal pode ser representado como soma de senóides → análise generalista;
- Etc.
Parâmetros de sinais sinusoidais
Amplitude A
A amplitude é o valor, propriamente dito, que a função senoidal assume no tempo.
Em um dado instante de tempo t, a amplitude do sinal naquele instante é chamada de Amplitude instantânea.
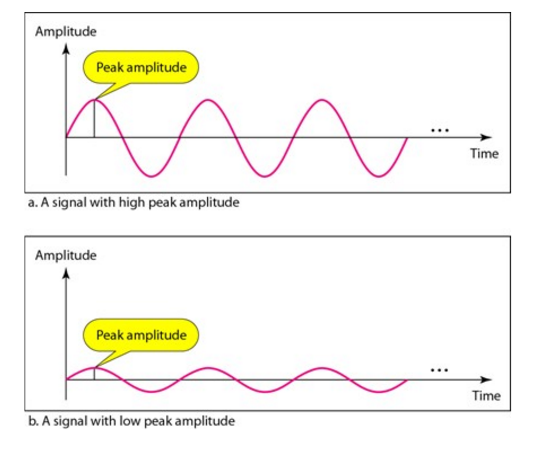
O maior valor de amplitude encontrado no sinal, em módulo, é chamado de Amplitude máxima, ou valor de pico.
Considerando-se dois ciclos consecutivos, a medida entre a amplitude máxima positiva e a amplitude máxima negativa é chamada de Valor pico-a-pico.
Unidade de amplitude de corrente: Ampere [A]
Unidade de amplitude de tensão: Volts [V]
Tempo t
O tempo num gráfico senoidal pode ser dado em segundos ou na forma angular.
A unidade para ângulos pode ser graus, ou radianos.
Unidade: segundo [s] ou radianos [rad]
Período T
Também chamado “comprimento de onda” - é o tempo de duração de um ciclo completo da senóide.
Um período, ou ciclo completo da senóide equivale a 360° ou 2π radianos.
Se um ciclo completo 2π corresponde ao período de tempo T:
2π - 360° x radianos - t graus
ou:
x = 2π.t/360° x = π.t/180
Unidade: segundo [s] ou radianos [rad]
Frequência f
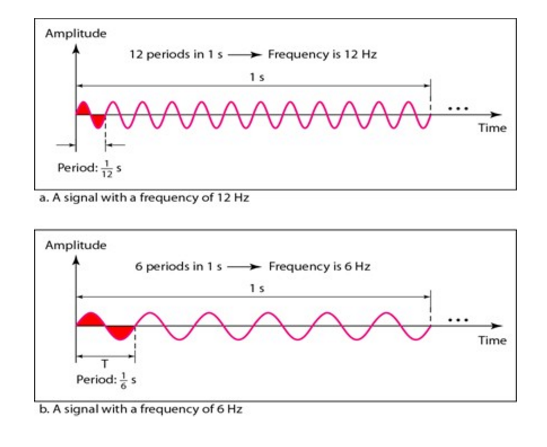
Corresponde ao número de ciclos que ocorrem por segundo.
Equivale a 1/T.
Unidade: Hertz [Hz]
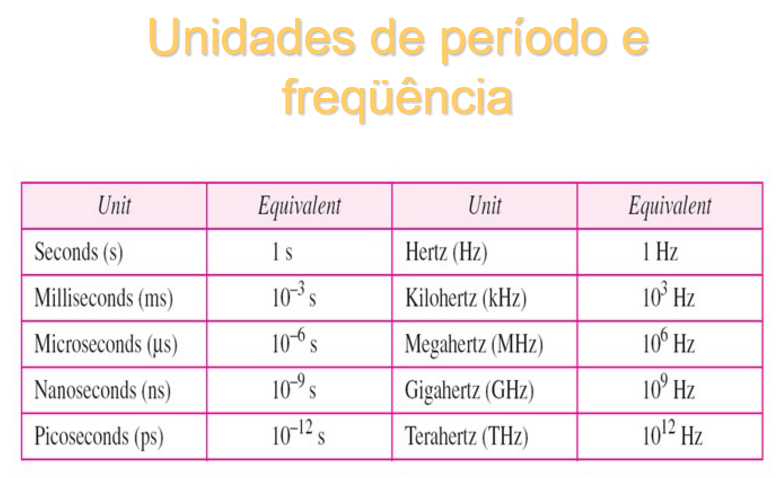
Conversão de unidades s e Hz
Frequência Angular ω
Pode ser vista como a Velocidade de “giro” do sinal senoidal ω = 2π/T, ou 2πf.
Unidade: Radianos por segundo [rad/s]
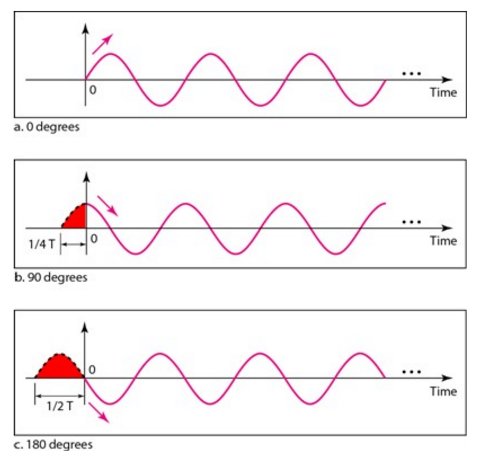
Fase θ
Descreve a posição da senóide em relação ao instante de tempo inicial (t=0).
A fase também é medida em graus [°] ou radianos [rad].
Note que sen(α + π/2) = cos(α)
Existem várias relações trigonométricas que inter-relacionam fase, senos e cossenos. Maiores informações: Relações trigonométricas
Tensão Senoidal instantânea
v(t) = Vp. sen(ω.t)
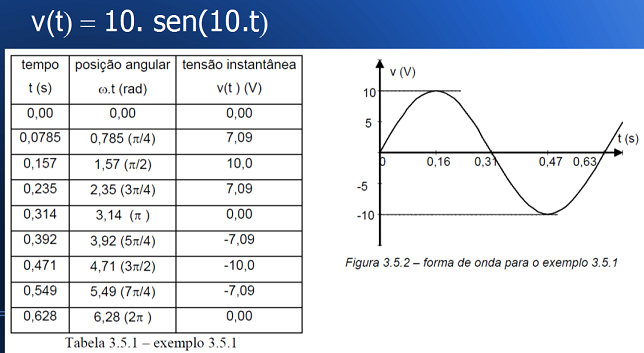
Exemplo
Faça o levantamento dos valores instantâneos de tensão para a equação senoidal abaixo:
Corrente Senoidal instantânea
i(t) = Ip. sen(ω.t)
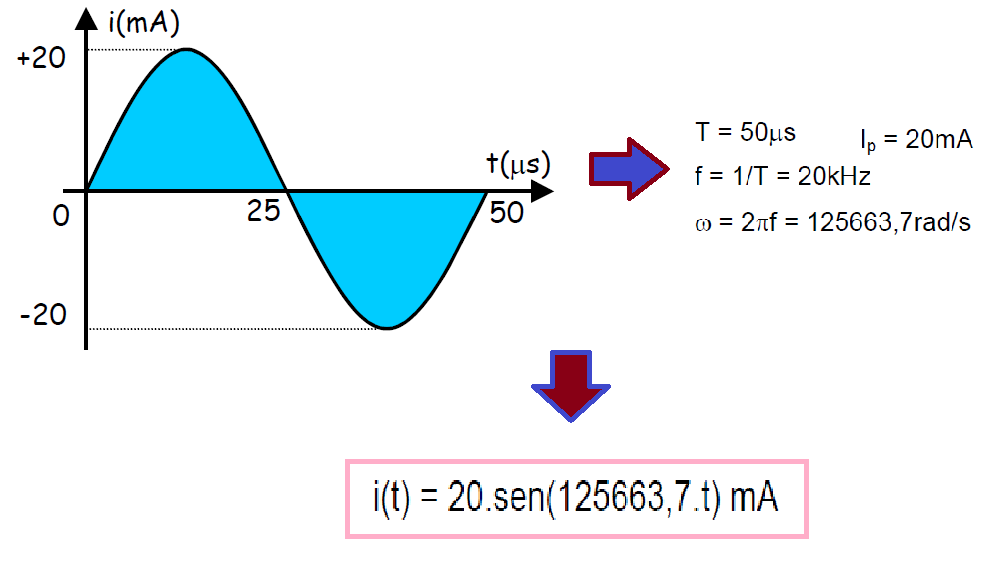
Exemplo
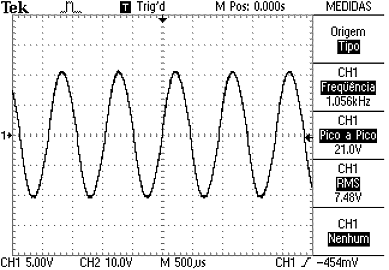
Obtenha a função matemática da forma de onda de corrente abaixo:
| << Página do curso | AULA 1 - Geração em corrente alternada - Função senoidal | Geração em corrente alternada - Valor médio e eficaz >> |
|---|