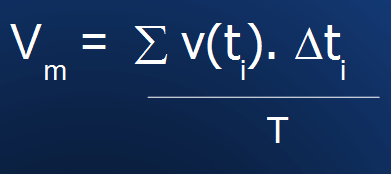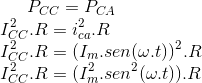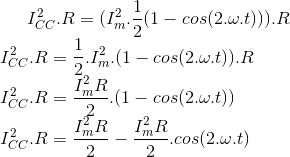AULA 2 - Circuitos 2 - Engenharia
<<< Voltar para página principal do curso
Valor médio
O valor médio de uma função representa o resultado líquido da variação de uma grandeza física como deslocamento, temperatura, tensão, corrente, etc.
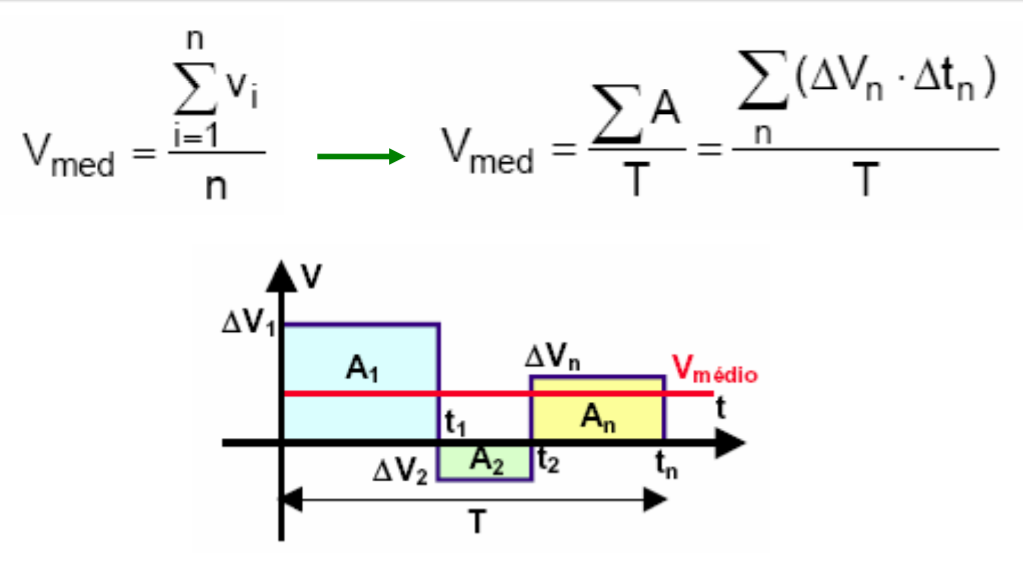
O valor médio de uma função discreta é calculado pela média aritmética dos valores, no tempo.
Em outras palavras:
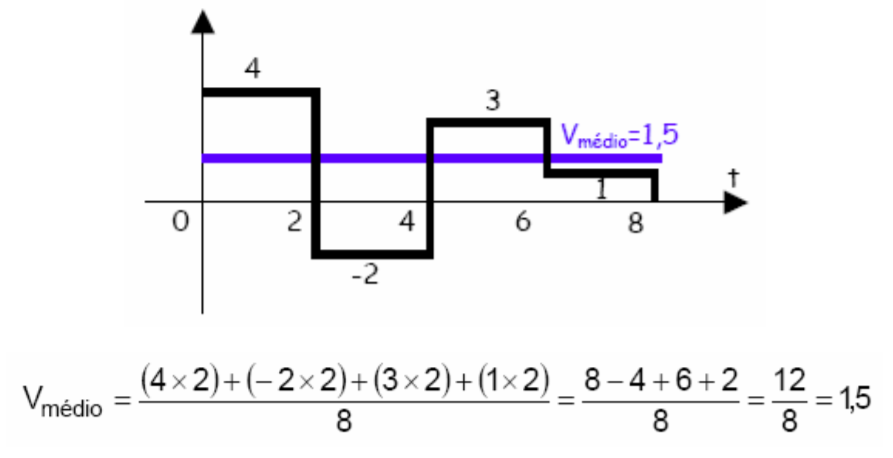
Exemplo 1
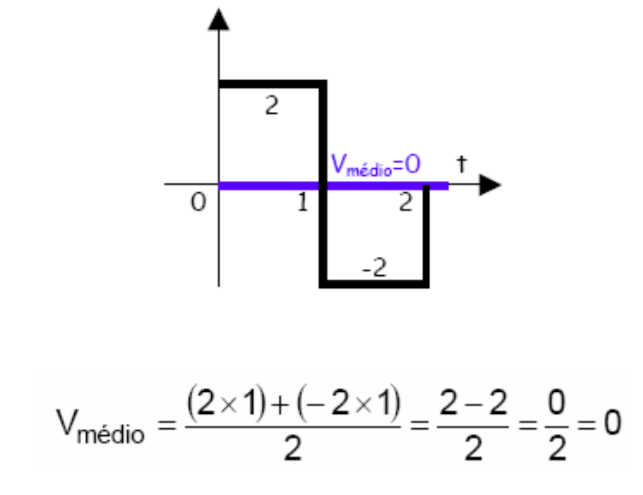
Exemplo 2
Valor médio de função senoidal contínua
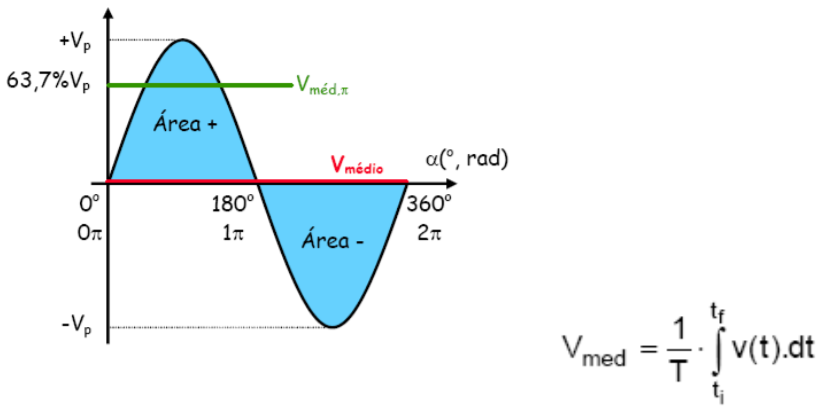
No caso particular das tensões e correntes senoidais e contínuas, a estimativa do valor médio vai envolver cálculo integral:
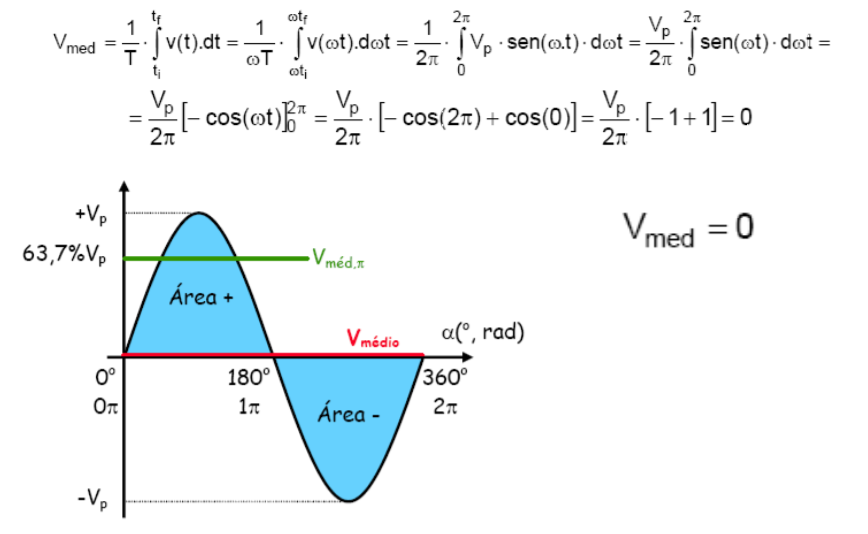
O problema é que a integral da senóide, o valor médio de uma função senoidal pura, para um período completo, de 0 a 2.π, é sempre NULA.
A área do semi-ciclo positivo é idêntica à área do semi-ciclo negativo. A soma de ambas é zero:
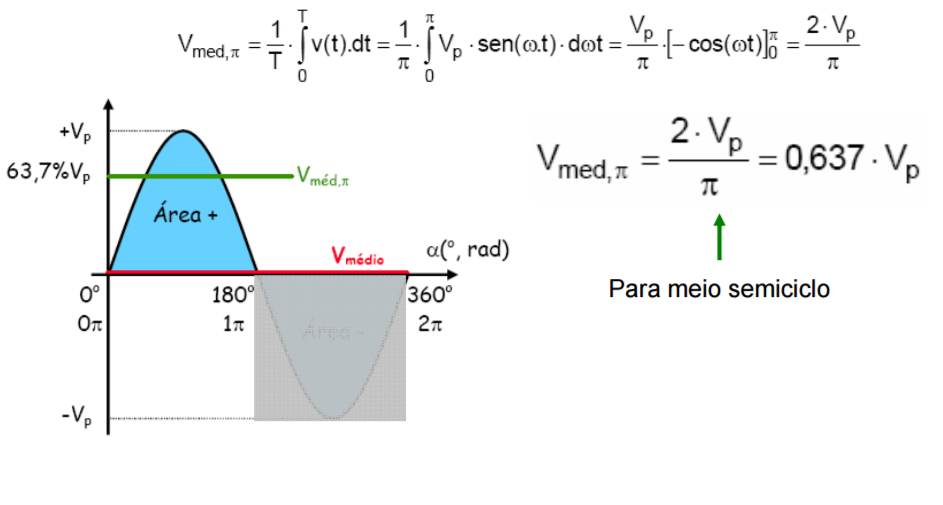
A análise de valor médio para apenas um semi-ciclo da senóide resulta em:
Valor eficaz
Vimos na seção sobre Valor Médio, que este é nulo, ao longo do período da senóide.
Isto levanta a seguinte questão:
Como é possível que uma corrente alternada forneça potência a um circuito, ao longo de um ciclo, se seu valor médio é zero????
À primeira vista, pode parecer que a potência fornecida durante o semi-ciclo positivo seria absorvida durante o semi-ciclo negativo; como as duas têm o mesmo valor absoluto, a potência total seria nula???!!!???
Não, porque se observa empiricamente que, independente do sentido e do valor de uma corrente através de um resistor, este dissipará potência sempre que alimentado por corrente alternada!!!
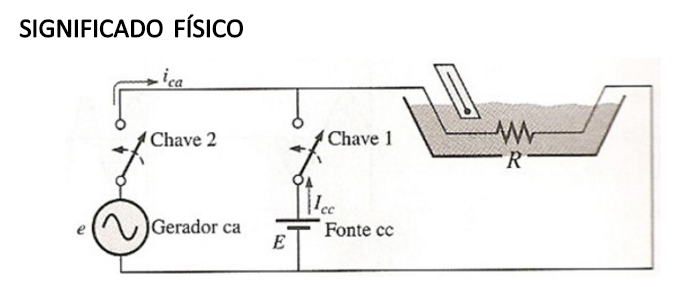
Para ilustrar este fenômeno, imagine o experimento abaixo:
Figura 1: Arranjo experimental para estabelecer uma relação entre grandezas CC e CA. (fonte: Boylestad)
A resistência R para aquecer a água é ligada por chaves a duas fontes: uma CC e outra, CA. A temperatura que a água vai atingir é função da potência dissipada (convertida em calor) pelo resistor.
Se a chave 1 for fechada (com a chave 2 aberta), uma corrente contínua Icc, que depende de R e da tensão E da bateria, atravessará R.
Se a chave 2 for fechada (com a chave 1 aberta), qual valor de tensão alternada tem que ser ajustada na fonte CA, para gerar a corrente ica que atravessará R, que aquecerá, para que a água do recipiente atinja a mesma temperatura (isto é, a mesma dissipação de potência)????
O problema resume-se, então, a encontrar os valores que satisfazem a equação abaixo:
mas:
sen² ω.t = ½(1 - cos 2ω.t)
portanto:
| << Geração em corrente alternada - função senoidal | AULA 2 - Geração em corrente alternada - Valor médio e eficaz | Geração em corrente alternada - Valor médio e eficaz >> |
|---|