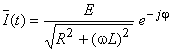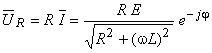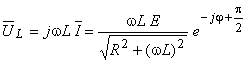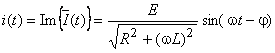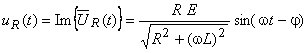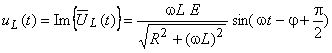AULA 6 - Circuitos 2 - Engenharia
<<< Voltar para página principal do curso
Resposta em Regime Senoidal para circuitos RC
Um circuito resistor-capacitor/condensador (circuito RC), filtro RC ou malha RC, é um dos mais simples filtros eletrônicos de resposta de impulso infinita analógicos.
Consiste de um resistor e de um capacitor/condensador, podendo estar ligados tanto em série quanto em paralelo, sendo alimentados, normalmente, por uma fonte de tensão.
Circuito RC Série
(Modificado de: e-Learning Tools for Electrical Engineering)
A seguir discutiremos o comportamento de um circuito elétrico contendo dois elementos: um resistor e um capacitor.
Figura 1 – Circuito RL série
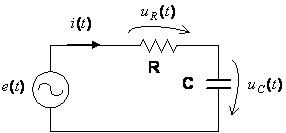
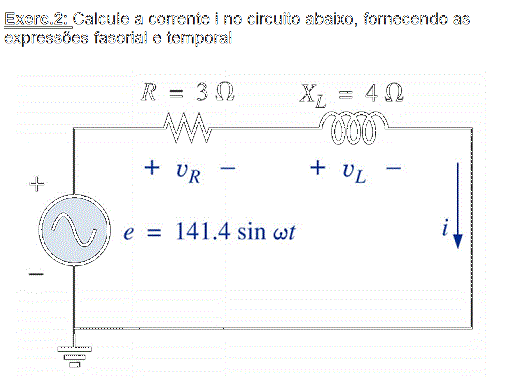
Considere-se o circuito RC série alimentado por uma fonte de tensão alternada sinusoidal cuja tensão é descrita pela expressão e(t) = E.sen(ωt).
Figura 2 – Esquema do circuito RL série com fonte senoidal
Conhecidos os valores de R e C, pretende determinar-se o regime permanente da evolução temporal da corrente no circuito, i(t), e das tensões aos terminais da resistência, 
, e da indutância, 
.
Através da Lei das Malhas, a soma da tensão nos terminais da resistência e nos terminais da bobina, será igual à tensão da fonte:
Em termos de amplitudes complexas a expressão anterior escreve-se:
onde R + j.ωL representa a impedância complexa do circuito, isto é, da resistência em série com a indutância.
Explicitando 
na expressão anterior, obtém-se:
com φ = arc tan (ωL)/R e 0 < φ < π/2.
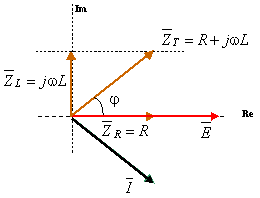
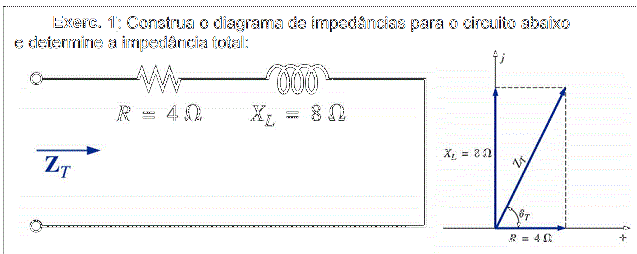
O diagrama fasorial da impedância, e amplitudes complexas da tensão da fonte e corrente, estão representados na figura abaixo.
Figura 3 – Diagrama fasorial das impedâncias
Note que a impedância complexa total é a soma vetorial dos fasores de resistência e da reatância indutiva.
Uma vez determinada a corrente, o cálculo da tensão no resistor é dado por:
que está em fase com a corrente.
Já a tensão nos terminais do indutor é:
A tensão complexa 
está avançada 90°, ou π/2 com relação a à corrente que a percorre.
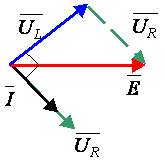
O diagrama fasorial completo das tensões e correntes do circuito, encontra-se representado na figura abaixo, onde se evidenciou a Lei das Malhas: a soma dos fasores 
e , os quais se igualam ao fasor da fonte 
.
Figura 4 – Diagrama fasorial das tensões e correntes do circuito RL
As expressões temporais para a corrente e tensões são dadas por:
,
e
com φ = arc tan (ωL)/R e 0 < φ < π/2.
As expressões que foram deduzidas admitiram que a tensão que alimenta o circuito tem uma fase inicial nula.
Porém, os diagramas fasorial e temporal que se obtêm são perfeitamente equivalentes aos obtidos quando se considera a tensão de alimentação com fase inicial nula; apenas diferem no instante a que se referem.
Exercícios
- Seções 13.6 a 13.8, do Boylestad, Pgs 403 a 405
- Seção 9.1, Exercícios 9.6 a 9.8, do Nilsson & Riedel, Pgs. 260 a 261
| << Circuitos RL | AULA 6 - Circuitos RC | Circuitos RLC >> |
|---|