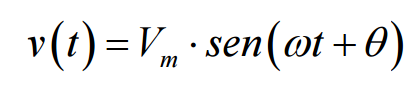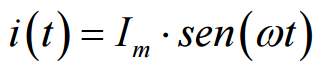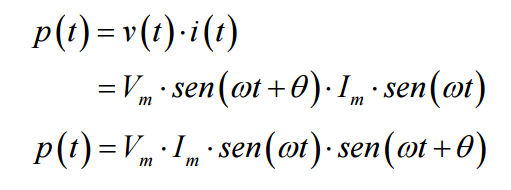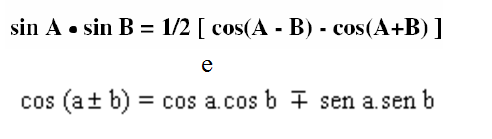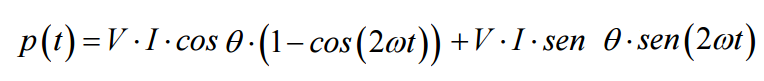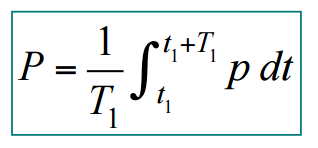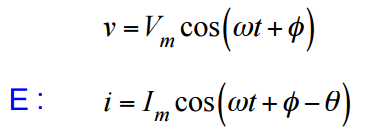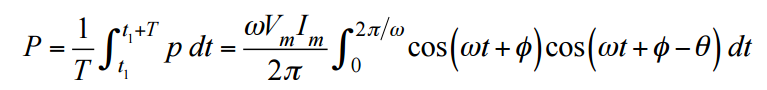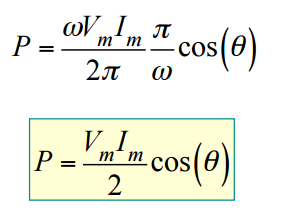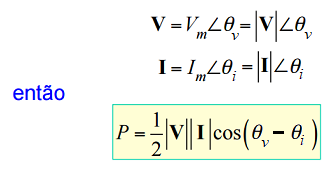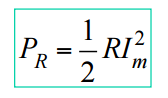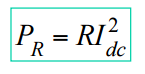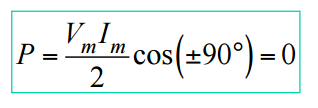AULA 11 - Circuitos 2 - Engenharia
Baseado no material sobre Retificadores e Circuitos Elétricos II, do Prof. Clóvis Petry, IFSC
Potência em CA regime permanente
Potência está diretamente ligado a trabalho e energia.
Podemos entender potência como a rapidez com que se realiza um determinado esforço ou trabalho. Por exemplo: se uma pessoa ergue 10Kg em 2 segundos e outra ergue os mesmo 10Kg, mas em 0,5 segundos, pode-se afirmar que a segunda pessoa realizou mais rapidamente o mesmo trabalho que a segunda.
Isso se chama potência.
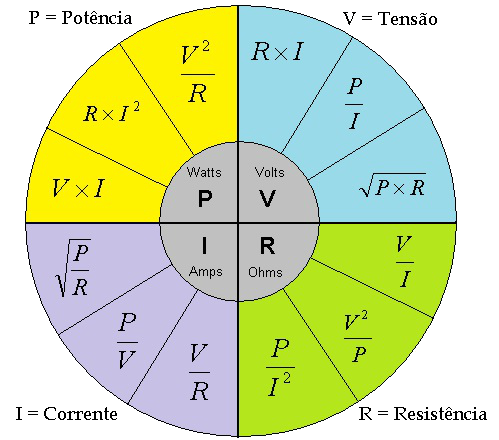
Em corrente contínua, a potência elétrica P é dada pela equação:
P = V. I
onde V é a tensão aplicada sobre a resistência R, e I é a corrente que a percorre.
Também pode ser expressa por:
P = R. I²
Ou seja, a potência CC está relacionada apenas ao gasto energético resistivo, porque as reatâncias são nulas, em ω = 0.
Em corrente alternada, tanto as tensões, quanto as correntes, são periódicas no tempo e, frequentemente, defasadas umas em relação às outras.
Portanto, não há um valor constante de potência para cada elemento resistivo, muito menos para cada elemento capacitivo ou indutivo.
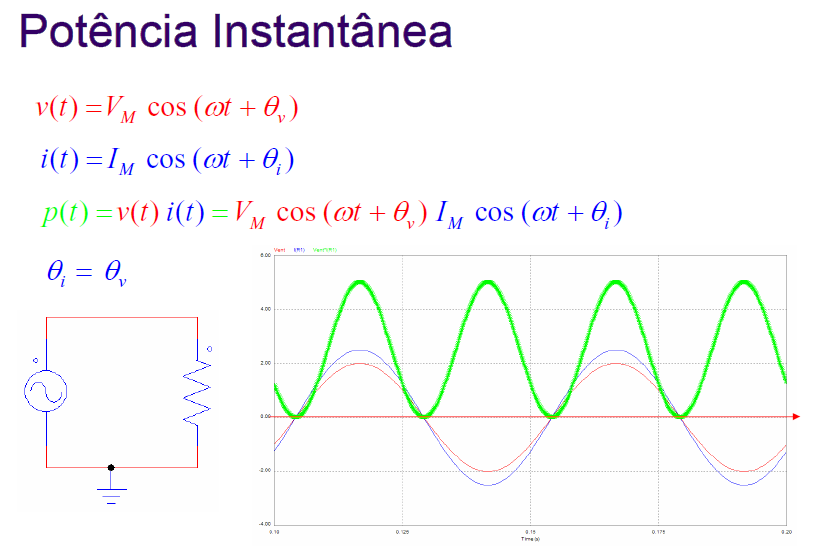
Potência instantânea
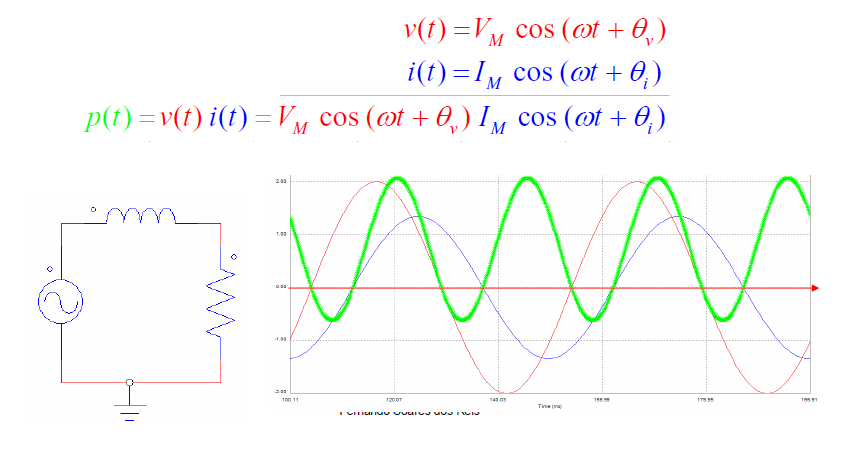
Seja um circuito CA, aonde a tensão v(t) é dada por:
e a corrente i(t), por:
a potência instantânea será, então, dada por:
mas:
e cos(-x) = cos(x), portanto:
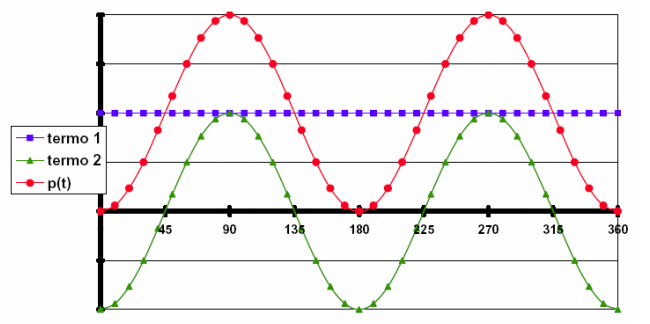
, isto é, a potência instantânea será composta por um termo constante no tempo (cos θ e sen θ) e um termo variável, função do tempo (cos (2.ωt - θ) e sen(2.ωt) ):
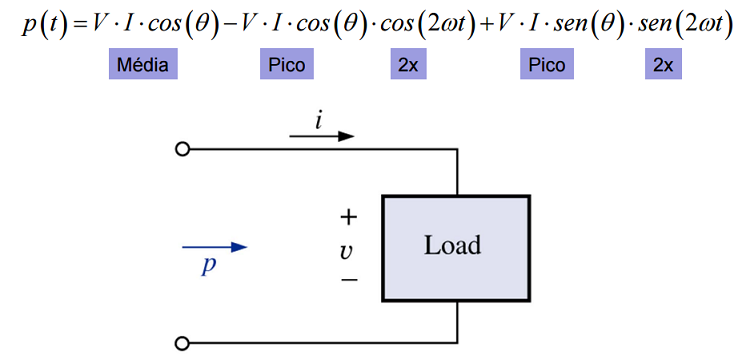
Reescrevendo-se, a potência instantânea total será dada por:
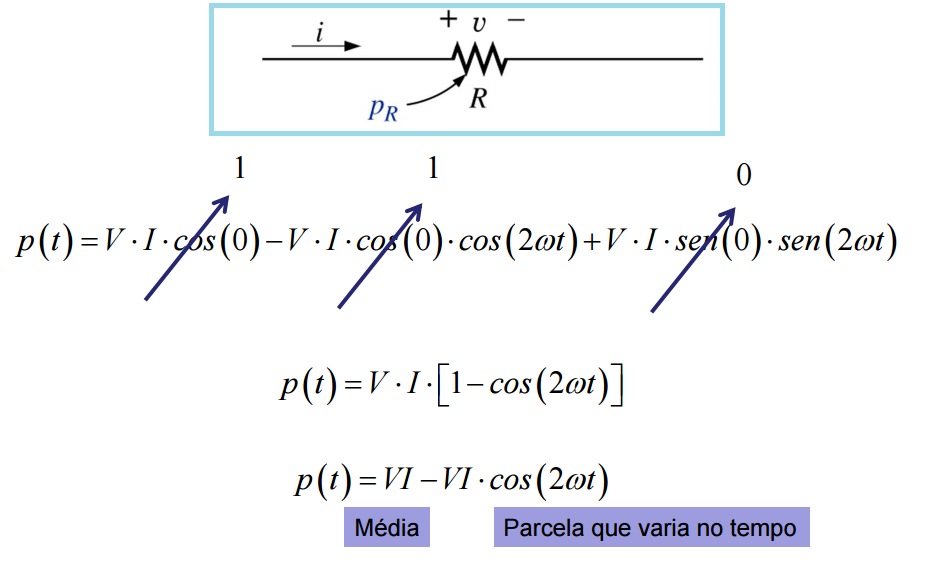
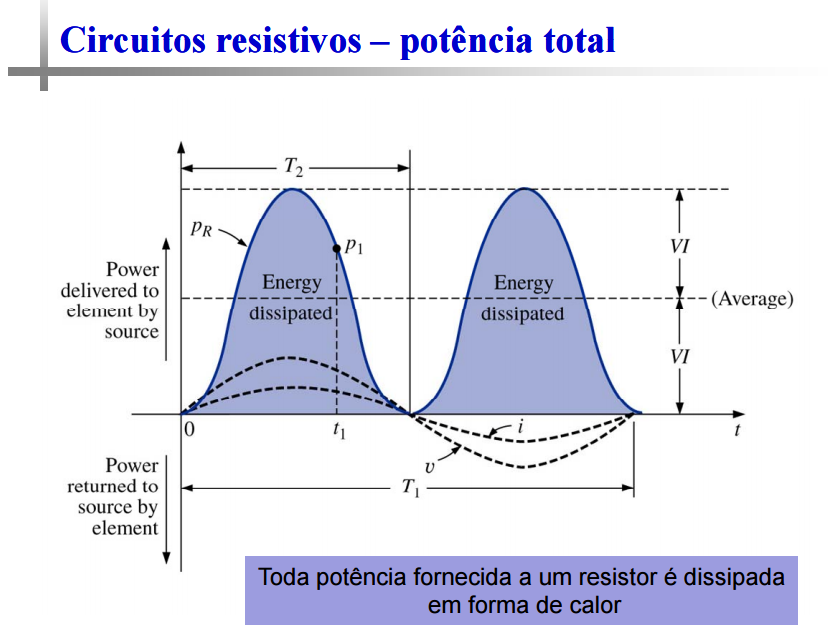
Potência instantânea no circuito resistivo puro
No circuito resistivo, a tensão e a corrente na resistência estão em fase, portanto, θ = 0:
Assim:
Se a alimentação for cossenoidal, o efeito será o mesmo:
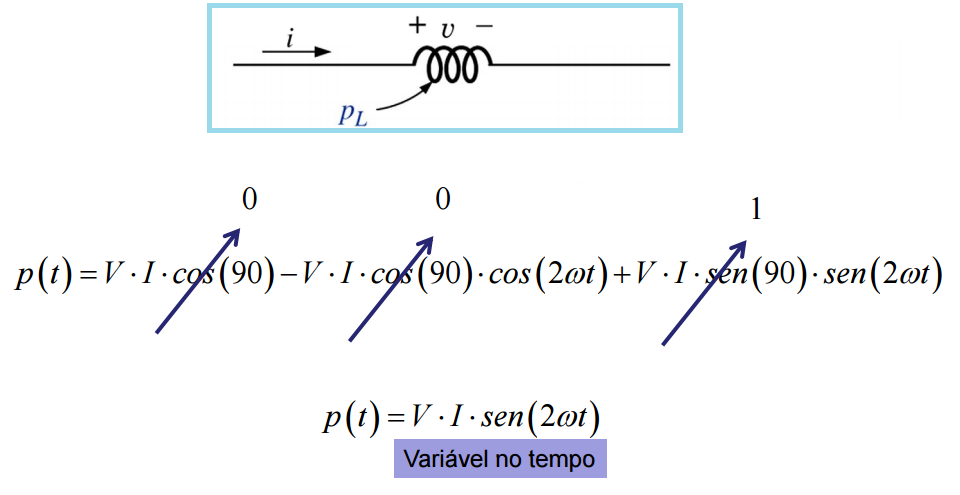
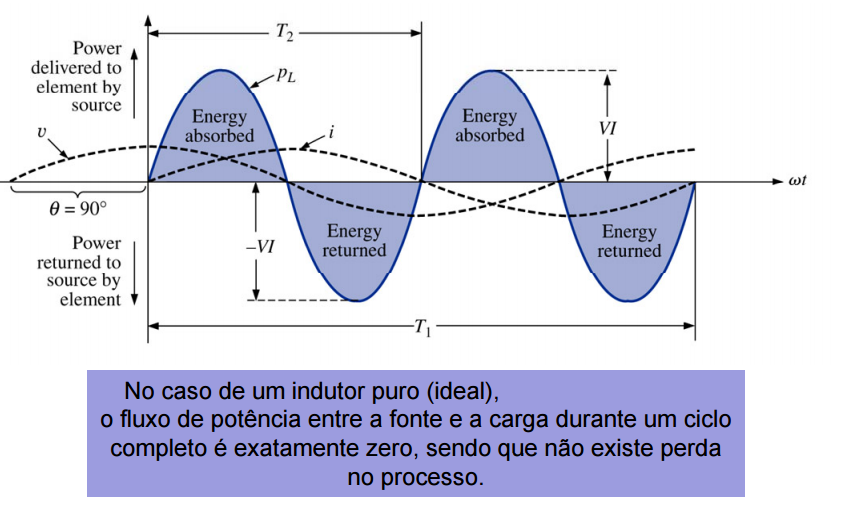
Potência instantânea no circuito indutivo puro
No circuito indutivo, a corrente está atrasada em relação à tensão, θ = 90:
Assim:
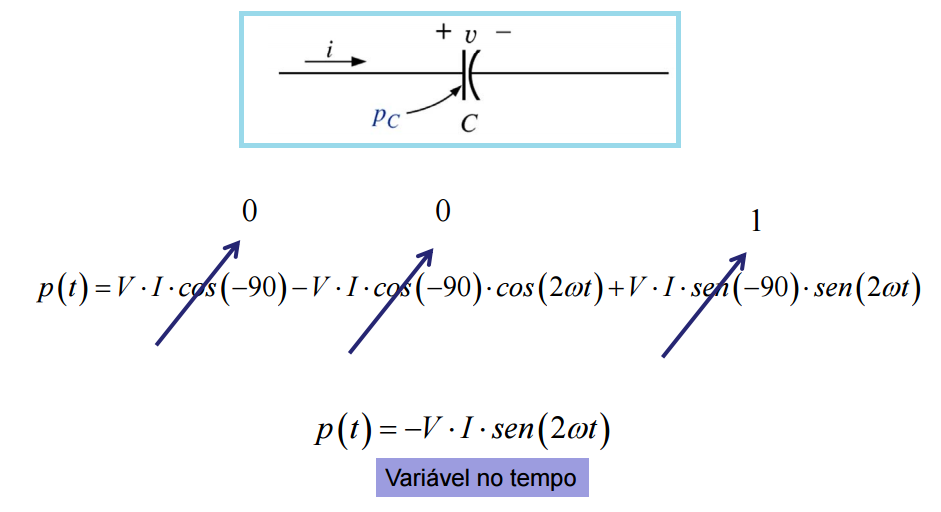
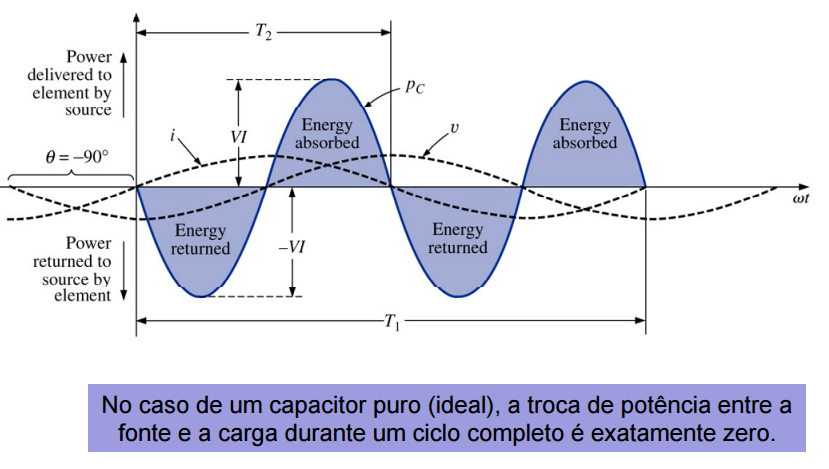
Potência instantânea no circuito capacitivo puro
No circuito capacitivo, a corrente está adiantada em relação à tensão, θ = -90:
Assim:
Potência instantânea no circuito misto
Assim como no circuito resistivo, haverá gasto energético (consumo de energia).
A potência instantânea terá que ser calculada em função dos valores de fase θv e θi da tensão e corrente em cada um dos elementos (impedâncias).
A potência instantânea, então, varia muito em circuitos CA.
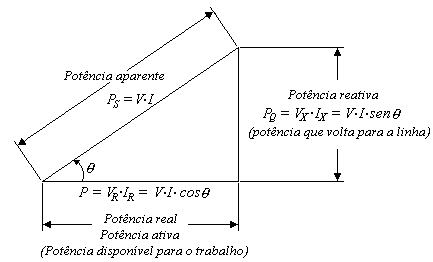
Ela pode ser decomposta em três componentes da potência elétrica: potências aparente, ativa e reativa.
- A potência Ativa, ou Média, é a que realiza Trabalho, de fato. Unidade é o Watt (W).
- A potência Reativa é aquela potência consumida por reatâncias (indutivas ou capacitivas) no armazenamento de energia, magnética ou elétrica, para o devido funcionamento do sistema elétrico. Unidade é o Volt-Ampère reativo (var).
- A potência Aparente é a potência total fornecida pela fonte. Unidade é o Volt-Ampère (VA).
A potência Aparente é calculada pela soma vetorial dos fasores de potências ativa e reativa:
Assim, conhecendo pelo menos duas grandezas dentre S, P, Q e fator de potência, é possível determinar as grandezas restantes utilizando trigonometria.
No caso da Potência Reativa, existe a dualidade entre os tipos de reatância, daí ser atribuído o sinal positivo à Potência reativa Indutiva e o negativo, à Potência reativa Capacitiva.
Entre essas potências existe uma relação conhecida como fator de potência (FP), determinada pelo cosseno do ângulo entre a potência ativa e a aparente, ou seja, P/S ou o cosseno do ângulo de fase, entre a tensão e a corrente.
Potência Média ou Ativa
Potência Média, ou Potência Ativa está relacionada à geração de calor, movimento ou luz.
Basicamente, ela pode ser considerada como a média da potência elétrica gerada por um único dispositivo com dois terminais.
É resultado do gasto energético após o início de cada processo de transmissão de energia, como o da corrente elétrica até os equipamentos que temos em casa, ou mesmo em máquinas industriais.
A potência ativa, que pode ser medida em watts (W) ou kilowatts (KW), por meio de um aparelho chamado wattimetro, é a energia que será realmente utilizada.
Potência média para uma potência instantânea periódica p é dada por:
Seja
A potência média entregue ao dispositivo, tomando t1 = 0 será:
mas da tabela de integrais de senoidais temos que:
portanto, Fazendo m = n = 1, α = φ e β = φ – θ, obtemos:
ou seja, a potência absorvida pelo bipolo é determinada pelas amplitudes Vm e Im e pelo ângulo θ pelo qual a tensão v antecede a corrente i.
A potência ativa pode ser vista, também, como a parte real da potência entregue à carga:
Em termos de fasores:
Potência ativa no resistor
Se o bipolo é um resistor, então θ = 0 e Vm = R.Im, assim:
Note que se i = Idc (corrente constante), então ω = φ = θ = 0 e Im = Idc, então,
Potência ativa no indutor e no capacitor
- Se o bipolo é um indutor, então θ = 90°.
- Se o bipolo é um capacitor, então θ = -90°.
Assim, para ambos os casos, temos:
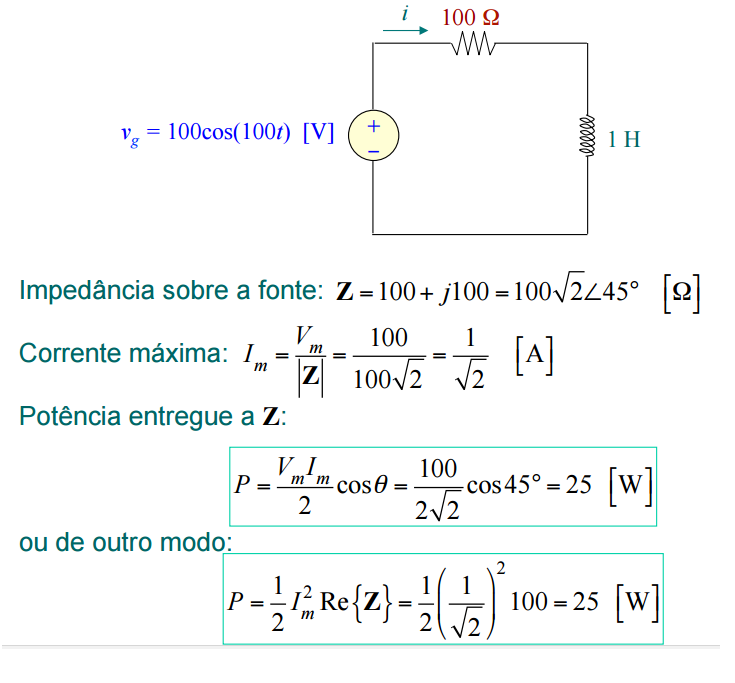
Exemplo:
Calcule a Potência ativa entregue pela fonte ao circuito abaixo:
Potência Reativa
A potência reativa, por sua vez, não realiza o trabalho em si.
Isso significa que não é essa energia que liga os eletroeletrônicos e outros equipamentos elétricos, mas ela funciona entre o gerador de energia e a carga em si, sendo responsável por manter o campo eletromagnético ativo em motores, reatores, transformadores, lâmpadas fluorescentes, etc.
Em outras palavras, é a potência usada apenas para criar e manter os campos eletromagnéticos das cargas indutivas ou capacitivas.
Sua medida é feita em VAR, que significa volts-Amperes-Reativos.
Numa instalação elétrica que apenas possua potência reativa, a potência ativa média tem um valor nulo, pelo que não é produzido nenhum trabalho útil. Diz-se portanto que a potência reativa é uma potência devatada (não produz watts ativos).
Na indústria elétrica recomenda-se que todas as instalações tenham um fator de potência ( {\displaystyle \cos \phi \,} \cos \phi \,) máximo, com o qual {\displaystyle \sin \phi \,} \sin \phi \, será mínimo e portanto a potência reativa ou não útil será também mínima.
A integração temporal da potência reativa resulta numa energia reativa, que representa a energia que circula de forma oscilante nas instalações mas não é consumida por nenhum receptor. Em casos de consumidores especiais de energia eléctrica (grandes consumidores), esta energia pode ser contabilizada em VAr-hora, e faturada adicionalmente à energia ativa consumida.