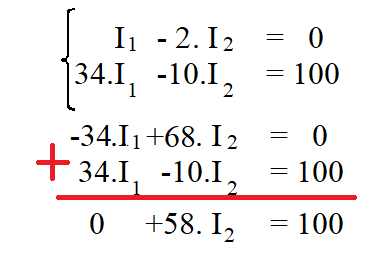AULA 11 - Eletricidade Básica - FIC

De IFSC
Revisão de 19h55min de 29 de setembro de 2022 por imported>Fargoud (→‎Análise Nodal Generalizada)
Ir para navegação Ir para pesquisar

<<< Voltar para página principal do curso



CARGA HORÁRIA: 5 h

CARGA HORÁRIA TEÓRICA: 4 h CARGA HORÁRIA PRÁTICA: 1 h


METODOLOGIA

  • Exposição dialogada dos conteúdos disponíveis, em projetor multimídia.
  • Navegação assistida em outros sites e portais, de conteúdos relacionados.
  • Montagens práticas e desenvolvimento em computador de aplicativos.
  • Testes de verificação e validação.



Análise Nodal Generalizada

Assim como no caso da Análise de Malhas, a Análise Nodal Generalizada é um método sistemático que permite analisar qualquer circuito, através das suas tensões de nós.

É mais apropriado para análise de circuitos com poucos nós e com fontes de corrente, ao invés de fontes de tensão!


O método consiste nos seguintes passos:


.

  1. Selecione um nó como referência e "aterre-o". O ideal é sempre escolher o nó com maior número de ramos conectados, porque isto diminui o número de equações no final
  2. Atribua tensões V1, V2, … , Vn-1 aos n – 1 nós restantes. Todas as tensões são medidas em relação ao nó de referência;
  3. Transforme as resistências em condutâncias;
  4. Aplique a LKC a cada um dos n – 1 nós que não são o de referência. Para expressar as correntes nos ramos, em termos de tensões nodais, adicione o termo (Vi - Vj).Gij para cada ramo, onde 'i' é o nó atual; e 'j' é o nó adjacente ao ramo.
  5. Para cada fonte de corrente do nó, adicione-a à equação, segundo a convenção:
    1. corrente da fonte entrando no nó - sinal negativo
    2. corrente da fonte saindo do nó - sinal positivo
  6. Resolva o sistema de equações, para obter as tensões nodais.
  7. Determine as correntes de interesse.


 * Você pode escolher o sentido horário, ou antihorário, porque, caso o sentido inicial tenha sido arbitrado errado, o sinal da corrente resultará em negativo, indicando que o sentido é o inverso. PORÉM, é extremamente recomendável que o sentido arbitrado para TODAS AS CORRENTES seja O MESMO: ou horário, ou anti-horário, sob pena de duas correntes terem seus sentidos arbitrados errado, e o erro de uma anular o erro da outra.

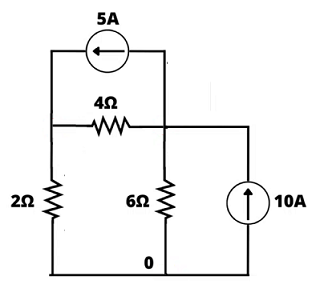
Exemplo 1: Análise Nodal - circuito 1

Analnodal1.png


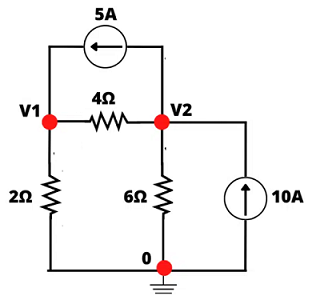
1) Selecione um nó como referência e "aterre-o".

2) Atribua tensões v1, v2, … , vn–1 aos n – 1 nós restantes. Todas as tensões são medidas em relação ao nó de referência;

Analnodal2.png

Ok!

3) Aplique a LKC a cada um dos n – 1 nós.

3.1) Nó 1:


  1. Resolva o sistema de equações, para obter as tensões nodais.
  2. Determine as correntes de interesse.

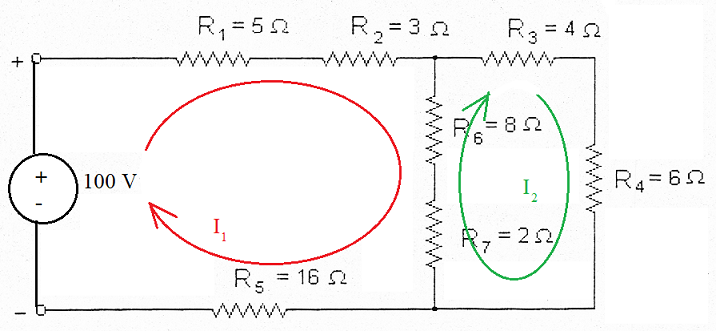
Exemplo 2: Análise Nodal - circuito 2

Analmalhas3.png

Este circuito contém duas malhas, então, a análise se dará como segue:

1) Arbitre uma corrente elétrica em cada malha 

→ Ok! Arbitradas as correntes I1 e I2;

2.1) Seguindo o sentido da corrente I1, compute o somatório das tensões na malha 1:

- 100 + R1.I1 + R2.I1 + R6.(I1 -I2) + R7.(I1 -I2) + R5.I1 = 0

Ou seja:

- 100 + 5.I1 + 3.I1 + 8.(I1 -I2) + 2.(I1 -I2) + 16.I1 = 0

- 100 + 8.I1 + 8.I1 -8. I2 + 2.I1 -2. I2 + 16.I1 = 0

- 100 + 34.I1 -10. I2 = 0 

34.I1 -10.I2  = 100 (Equação I)

2.2) Seguindo o sentido da corrente I2, compute o somatório das tensões na malha 2:

R7.(I2 -I1) + R6.(I2 -I1) + R3.I2 + R4.I2 = 0

Ou seja:

2.(I2 -I1) + 8.(I2 -I1) + 4.I2 + 6.I2 = 0

2.I2 - 2.I1 + 8.I2 -8.I1 + 4.I2 + 6.I2 = 0

- 10.I1 + 20.I2 = 0

20.I2 = 10.I1 


2.I2 = I1 (Equação II)


3)Resolva o sistema de equações 

→ 34.I1 -10.I2  = 100 

 → 2.I2 = I1

Existem várias maneiras de se resolver um sistema de equações. Por exemplo:

3.1) Por substituição:

Fazendo I1 = 2.I2 e substituindo-se em: 34.I1 -10.I2 = 100, teremos:

34.(2.I2) - 10.I2 = 100

68.I2 - 10.I2 = 100

58.I2 = 100

I2 = 100/58

→ I2 = 1,72 A

E, por consequência:

I1 = 2.I2

I1 = 2.1,72

→ I1 = 3,44 A

3.2) Resolvendo o sistema de equações por soma:

Sistequ1.png

E, assim por diante.

4) A corrente I3 será dada por I1 - I2 , portanto, 3,44 - 1,72 = 1,72 A


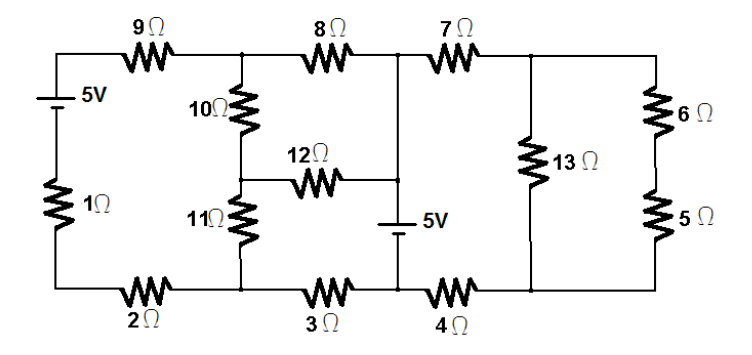
Exemplo 3: Análise de Malhas para circuito misto 2

Analmalhas5.png

Este circuito contém duas malhas, então, a análise se dará como segue:

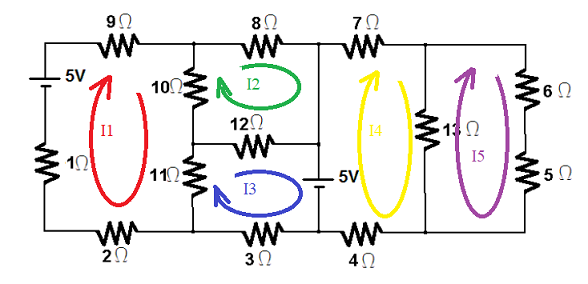
1) Arbitre uma corrente elétrica em cada malha


Analmalhas5-1.png


2.1) Seguindo o sentido da corrente I1, compute o somatório das tensões na malha 1:

2.I1 + 1.I1 -5 + 9.I1 + 10.(I1 - I2) + 11.(I1 -I3) = 0

33.I1 - 22.I2 = 5 (Equação I)

2.2) Seguindo o sentido da corrente I2, compute o somatório das tensões na malha 2:

10.(I2 -I1) + 8.I2 + 12.(I2 - I3) = 0

- 10.I1 + 30.I2 - 12.I3 = 0 (Equação II)


2.3) Seguindo o sentido da corrente I3, compute o somatório das tensões na malha 3:

11.(I3 -I1) + 12.(I3 -I2) +5 + 3.I3 = 0

- 11.I1 -12.I2 +26.I3 = -5 (Equação III)


2.4) Seguindo o sentido da corrente I4, compute o somatório das tensões na malha 4:

-5 + 7.I4+ 13.(I4 -I5) + 4.I4 = 0

24.I4 - 13.I5 = 5 (Equação IV)


2.5) Seguindo o sentido da corrente I5, compute o somatório das tensões na malha 5:

13.(I5 -I4) + 6.I5 + 5.I5 = 0

-13.I4 +24.I5 = 0 (Equação V)


3)Resolva o sistema de equações 

(I)   33.I1 - 22.I2 = 5 
(II)  -10.I1 + 30.I2  - 12.I3 = 0
(III) -11.I1 -12.I2  +26.I3 = -5
(IV)   24.I4 - 13.I5  = 5
(V)   -13.I4 +24.I5  = 0

Vamos começar pelas equações (I), (II) E (III), que se relacionam entre si

De (I), fazendo 33.I1 = 5 + 22.I2= I1= (5 + 22.I2)/33 = , e substituindo em (II), teremos:I1= 0,1515 + 0,66667.I2

-10.(0,1515 + 0,66667.I2) + 30.I2 - 12.I3 = 0

-1,1515 - 6,6667.I2 + 30.I2 - 12.I3 = 0

(VI) 23,3333.I2 -12.I3 = 1,1515

Substituindo I1= 0,1515 + 0,66667.I2 em (III), teremos:

-11.(0,1515 + 0,66667.I2) -12.I2 + 26.I3 = 0

-1,6667 -7,333.I2 -12.I2 + 26.I3 = 0

(VII) -19,333.I2 + 26.I3 = 1,6667


Multiplicando (VII) por 1,20:

23,3333.I2 -12.I3 = 1,1515

-23,3333.I2 +31,2.I3 = 2

0 + 19,2.I3 = 3,51

I3 = 3,51/19,2

→ I3 = 0,1828 A = 183 mA

Substituindo-se I3 em (VI):

23,3333.I2 -12.0,1828 = 1,1515

23,3333.I2 = 3,703

→ I2 = 0,159 A = 159 mA

De (I) :

I1= 0,1515 + 0,66667.0,159

→ I1= 0,2575 A = 257,5 mA

Agora, vamos investigar as duas correntes restantes: 

  24.I4 - 13.I5 = 5
 -13.I4 +24.I5  = 0

Multiplicando-se a segunda equação por 1,846:

24.I4 -13.I5 = 5 -24.I4 +44,3.I5 = 0

0 + 31,3.I5 = 5

I5 = 5/31,3

→ I5 = 0,159A = 159 mA

Substituindo-se em (IV):

24.I4 -13.0,159 = 5

24.I4 = 5 + 2,0766

→ I4 = 0,295A = 295 mA

Fontes Bibliográficas

COMISSÃO TRIPARTITE PERMANENTE DE NEGOCIAÇÃO DO SETOR ELÉTRICO NO ESTADO DE SÃO PAULO - CPN. Eletricidade Básica - Manual de treinamento curso básico segurança em instalações e serviços com eletricidade - NR 10 . Disponível em: https://portalidea.com.br/cursos/9f2909192195f210d6c6fa89c0894301.pdf

Lemes, Andryos da Silva. APOSTILA DE ELETRICIDADE BÁSICA. MINISTÉRIO DA EDUCAÇÃO, IFSP - CAMPUS DE PRESIDENTE EPITÁCIO. Disponível em:https://pt.scribd.com/document/280039386/Apostila-Eletricidade-Basica

ROCHA, Helder da. Introdução à Eletrônica para Artistas. Apostila de curso livre. 2017. Disponível em: http://www.argonavis.com.br/cursos/eletronica/IntroducaoEletronicaArtistas.pdf.

SAMBAQUI, ANA BARBARA KNOLSEISEN; TAQUES, BÁRBARA OGLIARI. Apostila de Eletricidade. MINISTÉRIO DA EDUCAÇÃO - IFSC - CAMPUS JOINVILLE. Joinville, agosto, 2010. Disponível em: http://wiki.itajai.ifsc.edu.br/images/c/c1/Apostila_de_Eletricidade_IFSC_JOINVILE.pdf

Souza, Giovani Batista. ELETRICIDADE. MINISTÉRIO DA EDUCAÇÃO - IFSC - CAMPUS ARARANGUÁ. Edição: fev, 2009. Disponível em: https://wiki.sj.ifsc.edu.br/images/e/e6/Aru-2009-Agosto-eletricidade_basica.pdf


<<< Voltar para página principal do curso

Análise de Malhas << AULA 11 - ANÁLISE NODAL GENERALIZADA xxx >>
Disponível em “https://wiki.ifsc.edu.br/index.php?title=AULA_11_-_Eletricidade_Básica_-_FIC&oldid=22414”