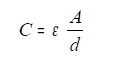AULA 12 - Eletricidade Básica - FIC

<<< Voltar para página principal do curso

CARGA HORÁRIA: 5 h

CARGA HORÁRIA TEÓRICA: 4 h CARGA HORÁRIA PRÁTICA: 1 h

METODOLOGIA

• Exposição dialogada dos conteúdos disponíveis, em projetor multimídia.
• Navegação assistida em outros sites e portais, de conteúdos relacionados.
• Montagens práticas e desenvolvimento em computador de aplicativos.
• Testes de verificação e validação.

Bipolos Passivos - Capacitor

Capacitores são componentes que acumulam carga elétrica.

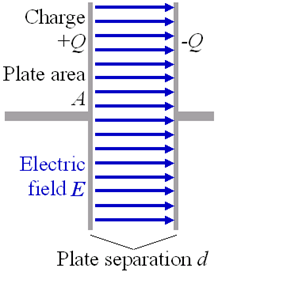
O formato típico de um capacitor consiste em dois eletrodos ou placas que armazenam cargas opostas. Estas duas placas são condutoras e são separadas por um isolante ou por um dielétrico.

A carga é armazenada na superfície das placas, no limite com o dielétrico. Devido ao fato de cada placa armazenar cargas iguais, porém opostas, a carga total no dispositivo é sempre zero.

Em circuitos onde flui corrente contínua, um capacitor age como um circuito aberto, impedindo a passagem de corrente, mas durante transições (ex: quando o circuito é ligado ou desligado) ou quando flui corrente alternada, o capacitor age como um condutor, deixando passar a corrente.

No esquema, um capacitor é representado por duas placas separadas. Alguns capacitores têm polaridade e precisam ser usados no circuito respeitando essa polaridade (o + ligado ao positivo e o – ligado ao negativo).

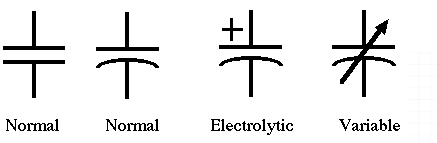
Os símbolos abaixo são usados para capacitores:

A Capacitância

A Capacitância é a propriedade que os capacitores têm de armazenar energia elétrica sob a forma de um campo eletrostático.

É a capacidade do capacitor de armazenar cargas (Q) nas placas, ou armaduras.

A carga elétrica armazenada em um capacitor é diretamente proporcional à diferença de potencial elétrico ao qual foi submetido.

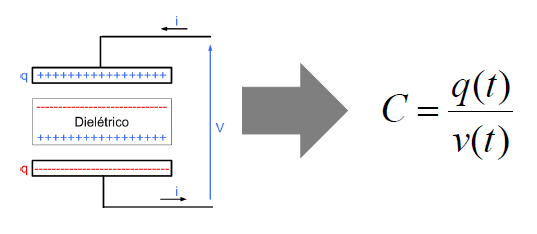
Assim sendo, definimos capacidade eletrostática C de um capacitor como a razão entre o valor absoluto da carga elétrica Q e a ddp V nos seus terminais.

   Q = C.V

Essa carga elétrica corresponde à carga de sua armadura, ou placa, positiva.

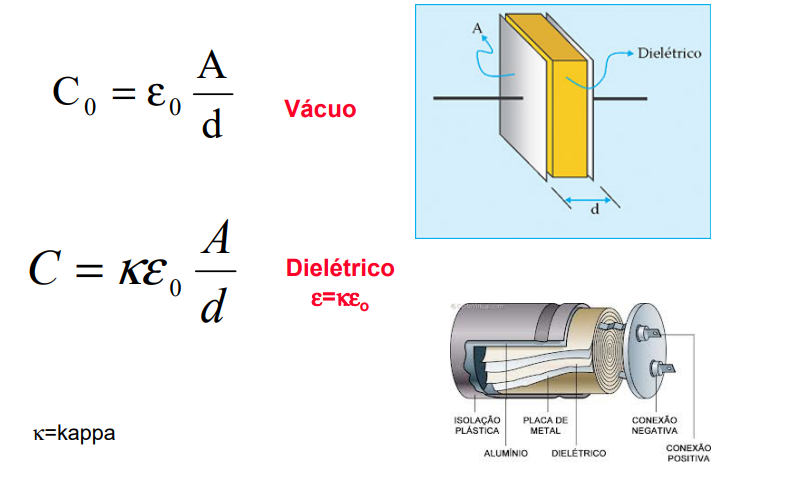
A capacitância é determinada pelos fatores geométricos A (área) e d (distância) das placas que formam o capacitor. Quando a área das placas é aumentada, aumenta a capacitância.

Da mesma forma quando a separação entre as placas aumenta, a capacitância diminui.

Então temos que a capacitância num capacitor de placas paralelas, como o mostrado na figura acima, contendo duas placas de área A e separadas por uma distância d, é dada por:

C = capacitância em Farad;

A = área das placas em m²;

d = distância entre as placas em m;

ε₀ é a permissividade do vácuo, dada por ε₀ = 8,85 x 10^-12 C²/Nm²

Se entre as placas for colocado algum material dielétrico (não-condutor) devemos substituir ε₀ pela permissividade ε do material dielétrico que foi colocado.

A constante dielétrica

O que acontece com o capacitor quando um material dielétrico é colocado no seu interior ?

O efeito provocado por um dielétrico pode ser resumido como:

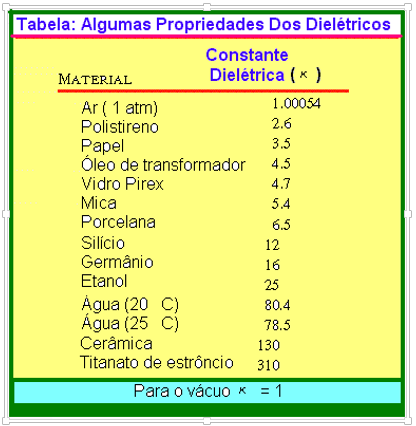
Numa região completamente preenchida por um dielétrico, todas as equações eletrostáticas que contém a constante de permissividade ε0 devem ser modificadas, substituindo-se aquela constante por κ.

Onde κ assume valores diferentes para materiais diferentes. Veja tabela,com valores de κ, para diversos materiais.

Constante dielétrica (κ) é, então, uma propriedade do material isolante utilizado em capacitores que influi na capacitância total do dispositivo.

Matematicamente, κ=C/C₀,ou seja,é a razão entre a capacitância C, obtida com uma determinada tensão no capacitor que contém um dado dielétrico e a capacitância C₀, obtida sem o dielétrico (vácuo).

Pode ser entendida como a relação entre um capacitor com determinado dielétrico e outro capacitor com mesmas dimensões, cujo dielétrico é o vácuo.

A constante dielétrica é adimensional.

Exemplo 1

Qual é a carga de um capacitor de 300 pF, quando ele é carregado em uma tensão de 1kV ?

Resposta: Q = 3 x 10^–7 C = 0,3 μC

Exemplo 2

Um capacitor armazena em suas placas uma carga de 40mC, quando submetido a uma d.d.p. de 20V. Determine a capacitância desse capacitor.

Exemplo 3

O que aconteceria, com a d.d.p. e com sua capacitância, se aproximarmos em duas vezes as placas do capacitor?

Exemplo 4

Um capacitor de placas paralelas, separadas por uma distância d, possui capacitância de 4,0 pF.

Sabendo que a área de suas placas é de 1,0 .10-2 m², e que cada placa armazena uma carga (em módulo) de 10μC, determine:

a) a tensão aplicada às suas placas. b) a distância d entre as placas do capacitor. c) a intensidade do campo elétrico criado entre as placas

Exemplo 5

Um capacitor de placas paralelas possui placas circulares de raio igual a 8,2 cm e separação de 1,3 mm, no vácuo

a) Determine a sua capacitância.

b) Se aplicarmos uma diferença de potencial de 120 V, qual será o valor da carga que surgirá sobre as placas.

c) Se entre as placas for colocado um material cerâmico, qual será a nova capacitância?

R.: a) C = 1,44 x 10 –10 F = 0,144 nF;

b) Q = 1,73 x 10 –8 C = 17,3 nC;

c) C = 1,87 x 10 –8 F = 18,7 nF.

Unidade de capacitância

A capacidade de carga de um capacitor é medida em farads, em homenagem ao cientista inglês Michael Faraday.

1 F = 1 Coulomb/Volt. 

Em geral usamos bilionésimos ou milionésimos de farad em nossos circuitos, às vezes ainda menos que isto.

Portanto os capacitores que usaremos são representados em microfarads (μF) (1/1000000), nanofarads (nF) (1/10⁹) e picofarads (pF) (1/10¹²).

Os capacitores eletrolíticos são polarizados, e têm valores maiores. A identificação deles é impressa na embalagem.

Já os capacitores de menor valor, cerâmicos e de poliéster, têm um código para representar o valor baseado em pF. O código é semelhante ao dos resistores, mas sem as cores. São três dígitos. Os dois primeiros representam dígitos do valor, e o terceiro o número de zeros. Por exemplo:

• 103 = 1, 0, 000 = 10000pF = 10kpF = 10nF
• 474 = 4, 7, 0000 = 470000pF = 470kpF = 470nF
• 225 = 2, 2, 00000 = 2200000pF = 2200kpF = 2200nF = 2,2 μF

Representação Gráfica da Capacitância

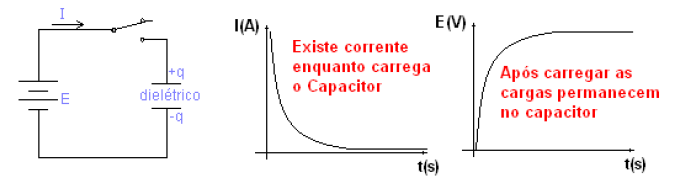
Existe uma relação entre a tensão aplicada entre duas placas paralelas separadas por um dielétrico, e a carga que aparece nestas placas.

Analise o circuito abaixo:

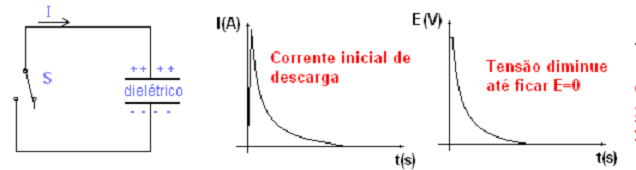
Na figura abaixo, considerando o capacitor carregado, ao acionarmos a chave S, o capacitor inicia o processo de descarga. No início existe fluxo de elétrons (corrente) até o capacitor se descarregar E =0.

Um gráfico relacionando a tensão e a carga acumulada gera uma relação linear. A constante de proporcionalidade entre a carga acumulada e a tensão, isto é, a inclinação da reta é a capacitância, desta afirmação temos:

Q = C.E

Associação de Capacitores

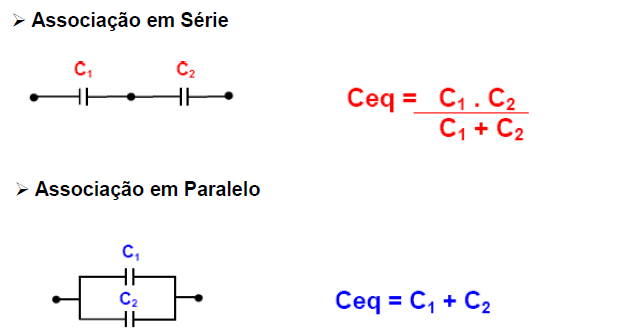
Dois ou mais capacitores estarão associados EM SÉRIE quando entre eles não houver nó, ficando, dessa forma, a armadura negativa de um ligada diretamente à armadura positiva do outro.

Ao estabelecermos uma diferença de potencial elétrico nos terminais da associação, haverá movimentação de elétrons nos fios que unem os capacitores até que estes estejam completamente carregados.

Ao ser conectada ao terminal positivo da pilha, a armadura do capacitor C1 fica eletrizada positivamente e induz uma separação de cargas no fio que o liga ao capacitor C2, atraindo elétrons para sua outra armadura que fica eletrizada negativamente e, conseqüentemente, eletrizando a armadura positiva do capacitor C2, que por sua vez induz uma separação de cargas no fio que une este ao capacitor C3, e assim por diante.

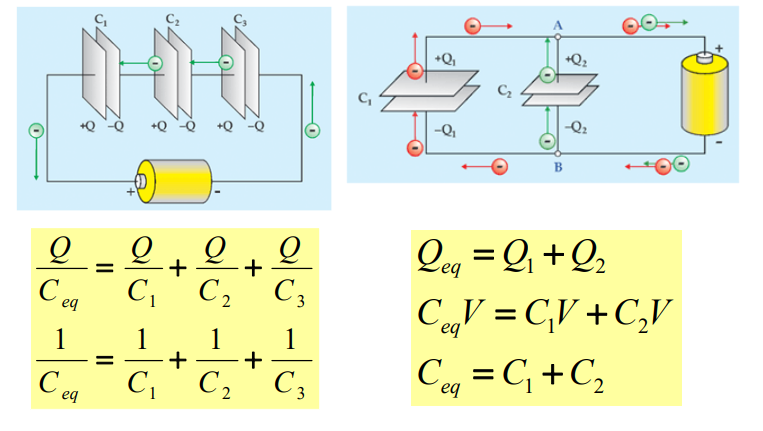
Esse fato nos permite concluir que, em uma ligação SÉRIE:

• todos os capacitores ficam carregados com a mesma carga elétrica Q;
• a carga elétrica armazenada na associação é igual a Q, pois foi essa quantidade que a pilha movimentou da armadura positiva do capacitor C1 para a armadura negativa do capacitor C3.

Dois ou mais capacitores estão associados EM PARALELO, quando seus terminais estão ligados aos mesmos nós e, conseqüentemente, sujeitos à mesma diferença de potencial U.

Na figura, os capacitores estão com seus terminais ligados aos mesmos nós A e B.

Conectando os nós A e B aos terminais da pilha, os capacitores ficam sujeitos à mesma ddp U e, se suas capacidades eletrostáticas forem diferentes, adquirem cargas elétricas Q1 e Q2 diferentes entre si.

As armaduras ligadas ao nó A cedem elétrons para a pilha e as ligadas ao nó B recebem elétrons da pilha, de modo que a carga elétrica total movimentada pela pilha, das armaduras positivas para as negativas, é igual à soma das cargas Q1 e Q2, até atingido o equilíbrio eletrostático.

Portanto, concluímos que:

• a carga elétrica Q armazenada na associação é igual à soma das cargas elétricas armazenadas em cada capacitor:

    Q = Q1 + Q2

• essa carga elétrica é igual à quantidade de carga elétrica movimentada pela pilha das armaduras positiva para as negativas dos capacitores da associação;
• por ser uma associação em paralelo, a ddp U nos terminais A e B da associação é a mesma para todos os capacitores.

Utilização de Capacitores

Os capacitores têm várias aplicações nos circuitos elétricos e eletrônicos. Uma das principais é a filtragem. Eles podem acumular uma razoável quantidade de cargas quando estão ligados a uma tensão. Quando esta tensão é desligada, o capacitor é capaz de continuar fornecendo esta mesma tensão durante um pequeno período de tempo, funcionando como uma espécie de bateria de curta duração.

Os Capacitores são dispositivos utilizados geralmente para armazenar energia. O capacitor embutido no “Flash” de uma maquina fotográfica, armazena energia lentamente durante o processo de carga. Esta energia é liberada rapidamente durante a curta duração do “Flash”. Outro exemplo, são os capacitores microscópicos que formam os bancos de memória dos computadores.

Práticas com capacitores

Carga e descarga

Capacitores são bastante usados em circuitos eletrônicos, para acumular tensão, gerar pulsos, configurar temporizadores, retificar corrente alternada, proteger circuitos de sobretensão, isolar sinais, etc. Eles serão usados em vários outros experimentos.

Um capacitor acumula carga assim que recebe um pulso de corrente elétrica.

Se um capacitor está ligado diretamente a uma fonte de tensão contínua, ele recebe sua carga quase instantaneamente, assim que a bateria for ligada no capacitor.

A descarga, curto-circuitando os terminais do capacitor também é praticamente imediata.

Para limitar o tempo de carga ou descarga de um capacitor, usa-se um resistor. O valor do resistor multiplicado pelo valor da capacitância corresponde ao tempo em segundos que leva para um capacitor totalmente descarregado atingir 63% de sua carga.

Isto é a chamada CONSTANTE DE TEMPO.

Aproximadamente, cinco vezes esse tempo corresponde à carga total do capacitor.

Portanto, a constante de tempo para um circuito formado por um resistor R e um capacitor C é

t = R.C

E o tempo de carga é:

5 x R.C

Por exemplo, para um capacitor de 100 μF (0,0001 F) em série com um resistor de 10k ohms tem uma constante de tempo de:

t = 0,001 x 10000 = 1 segundo

E o capacitor levará

5 x 1 = 5 segundos

para carregar (ou descarregar) completamente.

Experimento 1 - Carga e descarga de capacitores

Este experimento demonstra o efeito da carga e descarga em um capacitor.

Material necessário:

• 1 capacitor eletrolítico de 100μF
• Capacitores eletrolíticos de 1000μF, 470μF, 47 e 10μF
• 2 resistores de 10k Ω
• Resistores de 1k e 100k Ω
• Voltímetro
• Bateria ou fonte de 9V
• Duas chaves tácteis (botões de pressão)
• Protoboard, jumpers e fios, garras jacaré

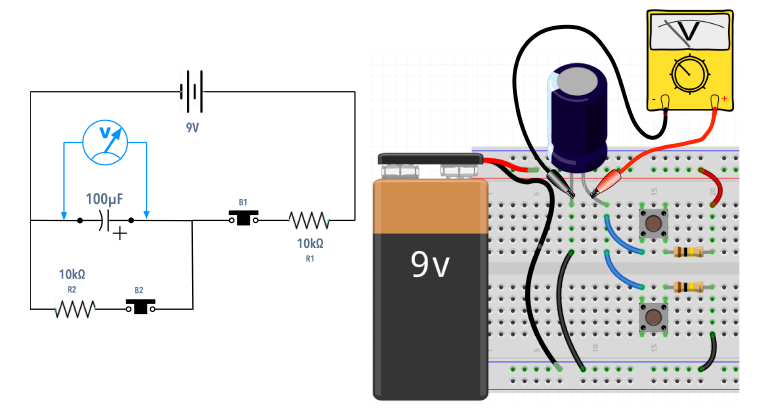
Monte o circuito abaixo.

O desenho das chaves no protoboard (de 4 terminais) podem estar diferentes das que você tem no kit (de 2 terminais).

Na dúvida use o esquema como referência para as conexões.

Antes de iniciar, meça a tensão da bateria, para saber o valor máximo de tensão que poderá ser carregado pelo capacitor.

Depois prenda o multímetro nos terminais do capacitor com garras jacaré, tendo o cuidado para não deixar que encostem uma na outra.

Apertando o botão B1 o circuito é fechado e a bateria começa a carregar através do resistor R1.

Segure o botão por uns 5 segundos ou até que o multímetro indique a tensão da bateria.

Agora solte o botão e perceba que a carga diminui muito lentamente (ela está vazando pelo voltímetro, que tem uma resistência muito alta).

Agora aperte o botão B2, que descarrega o capacitor através do resistor R2. Como os resistores são iguais, o tempo de carga e descarga é semelhante ao da carga. Experimente trocá-los por valores diferentes.

Troque também o capacitor de 100μF por capacitores maiores (470 e 1000 μF) e menores (47 e 10μF), e observe o resultado.

Para carregar ou descarregar rapidamente ligue as chave correspondente diretamente ao positivo ou negativo sem usar resistor, ou use resistores de valores baixos (100 Ω).

Usando a carga do capacitor para acender um LED

Material adicional:

• Um LED de qualquer cor
• Resistor de 470 Ω
• Capacitor de 2200 μF

Experimente ligar um LED em paralelo com o capacitor de 1000μF e veja como ele se comporta durante os estágios de carga e descarga (lembre-se que o LED não pode ser ligado diretamente; ele sempre precisa ter um resistor em série para limitar a corrente.)

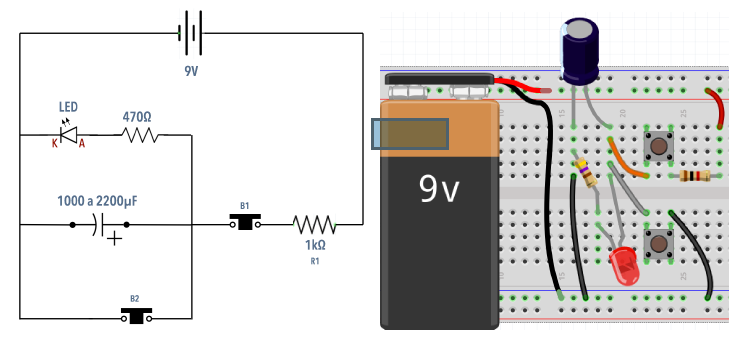
Veja uma possível solução no circuito abaixo:

Nesta configuração, o botão B2 descarrega o capacitor imediatamente através do fio. Mas ele também irá descarregar um pouco mais lentamente através do LED e resistor de 470 Ω.

Se você um resistor maior para limitar a corrente do LED (1k Ω) ele brilhará menos, mas ele também permanecerá aceso por mais tempo já que a resistência maior irá retardar a descarga do capacitor.

Experimente trocar o capacitor de 1000μF por um capacitor de 2200μF e troque o resistor R1 por uma ligação direta (para que a carga do capacitor seja imediata).

Experimente colocar os dois capacitores de 1000μF e 2200μF em paralelo. O que acontece?

Carregue o capacitor totalmente, depois desligue a bateria do circuito. Por quanto tempo o LED ainda permanece aceso?

Fontes Bibliográficas

COMISSÃO TRIPARTITE PERMANENTE DE NEGOCIAÇÃO DO SETOR ELÉTRICO NO ESTADO DE SÃO PAULO - CPN. Eletricidade Básica - Manual de treinamento curso básico segurança em instalações e serviços com eletricidade - NR 10 . Disponível em: https://portalidea.com.br/cursos/9f2909192195f210d6c6fa89c0894301.pdf

Lemes, Andryos da Silva. APOSTILA DE ELETRICIDADE BÁSICA. MINISTÉRIO DA EDUCAÇÃO, IFSP - CAMPUS DE PRESIDENTE EPITÁCIO. Disponível em:https://pt.scribd.com/document/280039386/Apostila-Eletricidade-Basica

ROCHA, Helder da. Introdução à Eletrônica para Artistas. Apostila de curso livre. 2017. Disponível em: http://www.argonavis.com.br/cursos/eletronica/IntroducaoEletronicaArtistas.pdf.

SAMBAQUI, ANA BARBARA KNOLSEISEN; TAQUES, BÁRBARA OGLIARI. Apostila de Eletricidade. MINISTÉRIO DA EDUCAÇÃO - IFSC - CAMPUS JOINVILLE. Joinville, agosto, 2010. Disponível em: http://wiki.itajai.ifsc.edu.br/images/c/c1/Apostila_de_Eletricidade_IFSC_JOINVILE.pdf

Souza, Giovani Batista. ELETRICIDADE. MINISTÉRIO DA EDUCAÇÃO - IFSC - CAMPUS ARARANGUÁ. Edição: fev, 2009. Disponível em: https://wiki.sj.ifsc.edu.br/images/e/e6/Aru-2009-Agosto-eletricidade_basica.pdf

---

<<< Voltar para página principal do curso

Análise de Nós <<	AULA 12 - CAPACITORES	Indutores >>