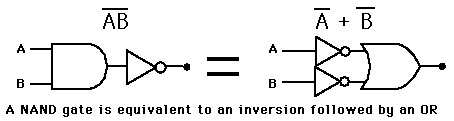AULA 6 - Eletrônica Digital 1 - Graduação
No capítulo anterior ficou evidente que minimizar circuitos eletrônicos é uma ARTE, antes de uma técnica!
É necessário dominar-se todos os teoremas, pra se ter garantia de ter chegado ao circuito ótimo.
Mas, além dos 20 teoremas citados no capítulo anterior, existem outras estratégias que permitem manipular as expressões, na tentativa de se eliminar termos.
Uma destas estratégias é a aplicação dos Teoremas de De Morgan.
1o. Teorema de De Morgan
O primeiro teorema de De Morgan estabelece que:
INV(A . B) = A' + B'
Graficamente:
2o. Teorema de De Morgan
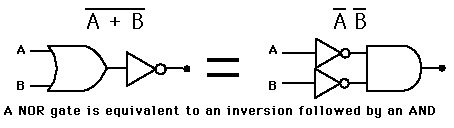
O segundo teorema de De Morgan estabelece que:
INV(A + B) = A' . B'
Graficamente:
Uso dos teoremas de De Morgan
A principal aplicação dos teoremas de De Morgan é permitir a manipulação das expressões booleanas, de forma a simplificá-las consideravelmente. Isto também devido à propriedade das portas inversoras de que:
Ora, assim é possível aplicar-se os teoremas a qualquer operação de soma (OU) e de multiplicação (E) lógicas, bastando, para isto, barrar duas vezes a expressão.
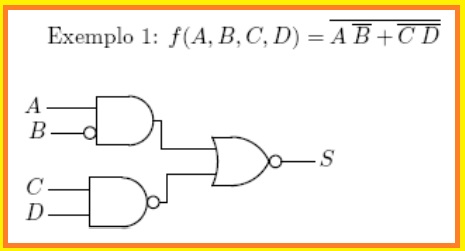
Exemplo 1
Aplique os teoremas de De Morgan ao circuito abaixo, de forma a minimizá-lo, se possível.
Este circuito é composto, originalmente, de:
- uma porta NOT (CI 7404);
- uma porta AND (CI 7408);
- uma porta NAND (CI 7400);
- e uma porta NOR (CI 7402).
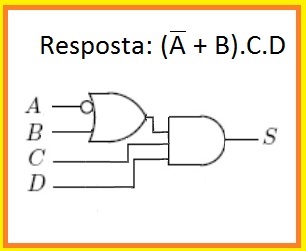
Resolução:
Circuito resultante (com redução de um porta NAND):
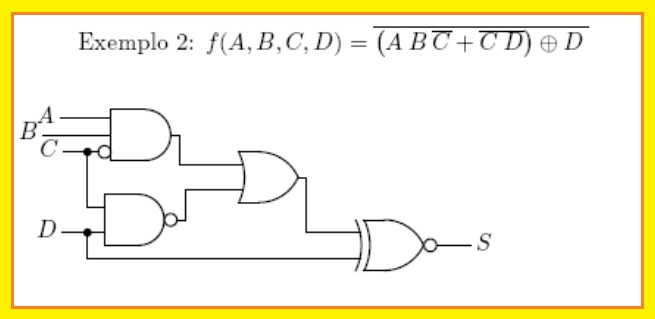
Exemplo 2
Aplique os teoremas de De Morgan ao circuito abaixo, de forma a minimizá-lo, se possível.
Este
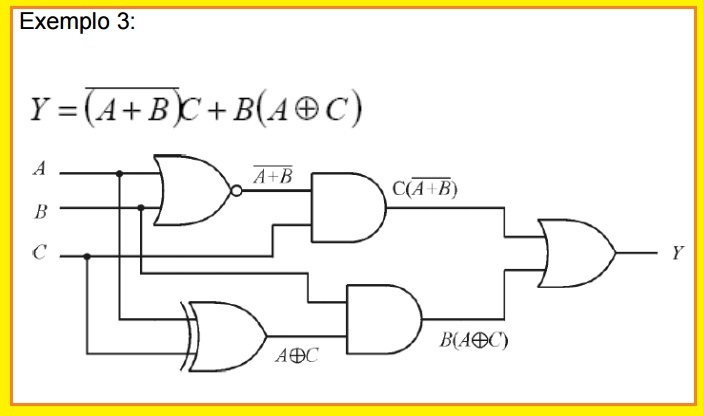
Exemplo 3
Aplique os teoremas de De Morgan ao circuito abaixo, de forma a minimizá-lo, se possível.
Este circuito é composto, originalmente, de:
- duas portas AND (CI 7408);
- uma porta NOR (CI 7402);
- uma porta XOR (CI 7486);
- e uma porta OR (CI 7432).
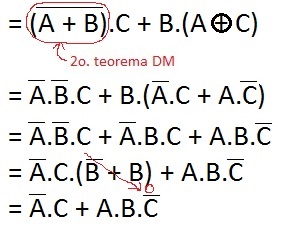
Resolução:
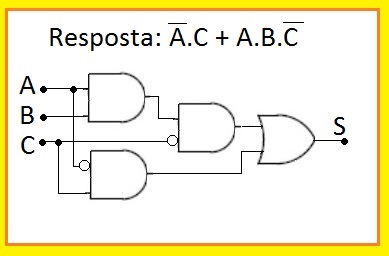
Circuito resultante, contendo apenas 1 CI 7408 (AND de 2 portas), 1 CI 7404 (inversora) e 1 CI 7432 (1 porta OR):