AULA 7 - Eletrônica Digital 1 - Graduação
<<= Voltar para a página principal do curso
Simplificação Algébrica
Existem várias técnicas para simplificar e reduzir circuitos lógicos.
A partir deste capítulo, serão vistas duas forma de simplificar circuitos:
- Fatoração
- Diagramas de Veitch-Karnaugh
Como visto, os circuitos lógicos correspondem (executam) expressões booleanas, as quais representam problemas no mundo real.
Porém, os circuitos gerados por tabelas verdade muitas vezes admitem simplificações, o que reduz o número de portas lógicas; essa redução diminui o grau de dificuldade na montagem e custo do sistema digital.
O estudo da simplificação de circuitos lógicos requer o conhecimento da álgebra de Boole, por meio de seus postulados, propriedades, equivalências, etc.
De fato, na álgebra de Boole encontram-se os fundamentos da eletrônica digital de circuitos.
Vimos que:
É imprescindível conhecer-se todos estes postulados e propriedades da Álgebra Booleana.
Como cada circuito corresponde a uma expressão, simplificações de expressões significam em simplificações de circuitos
Veremos, a seguir, o processo de fatoração.
Fatoração
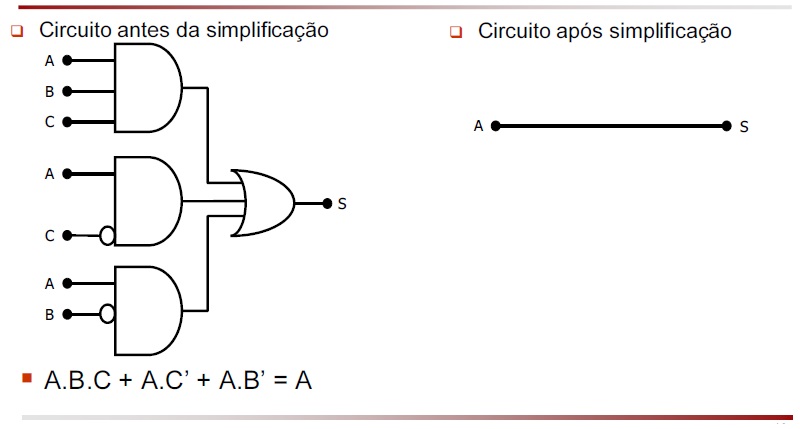
Consiste na aplicação dos postulados e propriedades da álgebra booleana, com o objetivo de simplificar a expressão.
Por exemplo:
Existem várias formas de se resolver a mesma simplificação. O importante é conhecer o máximo de postulados e propriedades aplicáveis.
Exercícios
| << Teoremas de De Morgan | AULA 7 - Simplificação Algébrica | Mapas de Karnaugh >> |
|---|