<<= Voltar para a página principal do curso

Exercícios de Simplificação Algébrica

Como visto, os circuitos lógicos correspondem (executam) expressões booleanas, as quais representam problemas no mundo real.

Porém, os circuitos gerados por tabelas verdade muitas vezes admitem simplificações, o que reduz o número de portas lógicas; essa redução diminui o grau de dificuldade na montagem e custo do sistema digital.

O estudo da simplificação de circuitos lógicos requer o conhecimento da álgebra de Boole, por meio de seus postulados, propriedades, equivalências, etc.

De fato, na álgebra de Boole encontram-se os fundamentos da eletrônica digital de circuitos.

Vimos que:

É imprescindível conhecer-se todos estes postulados e propriedades da Álgebra Booleana.

Como cada circuito corresponde a uma expressão, simplificações de expressões significam em simplificações de circuitos

Veremos, a seguir, o processo de fatoração.

Fatoração

Consiste na aplicação dos postulados e propriedades da álgebra booleana, com o objetivo de simplificar a expressão.

Por exemplo:

Existem várias formas de se resolver a mesma simplificação. O importante é conhecer o máximo de postulados e propriedades aplicáveis.

Exercícios Resolvidos

>> Solução do Exercício

Exercícios Resolvidos 2

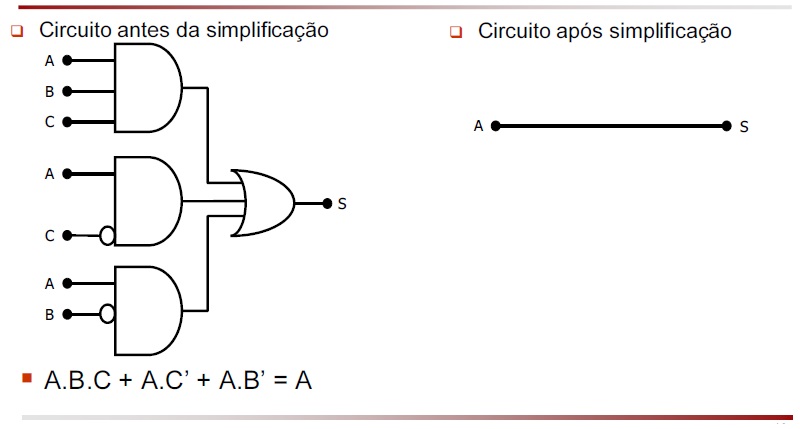
S = ABC + AC' + AB'
S = (ABC').(A' + B' + C')
S = (A + B + C).(A' + B' + C)
S = ((AC)' + B + D)' + C.(ACD)'
S = [(A + B).C]' + [D .(C + B)]'
S = A'B'C + A'BC + A'BC' + ABC + ABC'
S = A'B + AB' + AB
S = [X'Y'Z'. (X + Y + Z')]'
S = X'.(X + Y) + Z' + ZY
S = (A + B' + AB).(A + B').(A'B)
S = (A + B' + AB').(AB + A'C + BC)
S = (AB + C + D).(C + D').(C + D' + E)
S = A'B. (D' + DC') + (A + A'CD).B
V = (W + X + Y).(W + X' + Y).(Y' + Z).(W + Z)

>> Solução do Exercício 2

Exercícios Propostos

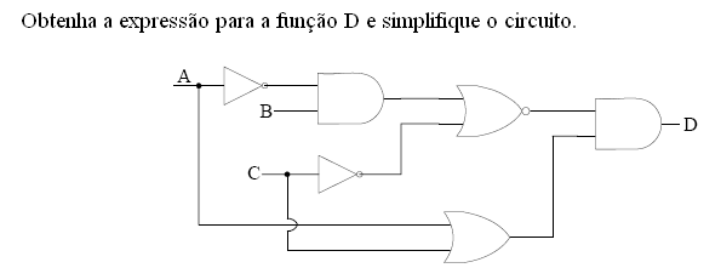
Y = A'.B'.C' + A'.B'.C + A'.B.C + A.B'.C . (Solução: Y = A'.B' + B'.C + A'.C)
Y = A.B + (A.B)'.C + (A + (B + C)')' . (Solução: Y = B + C)
Y = (A + B' + C' + D)' . (A' + B' + C' + D) + ((A'.B.C.D + (A'.B'.C.D)' + (A.B'.C.D')')' . (Solução: Y = A'.B.C.D')
Y = ((A.(B + C)')' + D)' + A.(B.C.D)' + (A'.B)'.(C'.D)' . (Solução: Y = A + B'.C + B'.D')