AULA 4 - Eletrônica Geral 1 - Técnico
Aplicações de Diodos em c.a.
Sinais
Um sinal é um meio de representar as informações contidas em fato ou fenômeno físico presentes em nosso mundo.
Na área técnica, tratamos como sinal todo fenômeno que carrega informações úteis a um processo ou sistema. Como exemplo, imagine que um sistema de controle tem que controlar a temperatura de um forno industrial, para esse sistema as informaçaões referentes àa variação da temperatura da câmara ao longo do tempo é um sinal, assim como as informaçaões de pressão, vazão de combustível, etc. Para um sistema de transmissão de rádio, um tipo de sinal seria a voz do locutor, a qual transporta as notícias a serem anunciadas. Um tipo de processo pode receber informaçaões advindas de vários sinais, alguns úteis, como os exemplificados acima, outros, indesejáveis. Normalmente trata-se os sinais indesejados em um determinado processo como ruído. Os sistemas eletrônicos a serem discutidos nessa apostila tem como intuito principal processar os sinais necessários para o funcionamento de um processo. No entanto, os sistemas eletrônicos apenas interpretam grandezas elétricas, como tensão e corrente. Assim sendo, para que os diversos fenômenos físicos possam ser processados é necessário que estes sejam primeiramente convertidos em sinais análogos de corrente ou tensão. Esse processo de conversão é realizado por equipamentos específicos chamados de transdutores, dos quais podemos citar o microfone (transdutor de pressão), o termopar (transdutor térmico), o LDR (transdutor luminoso), entre outros. Os transdutores mais utilizados em processos industriais serão tema das disciplinas de instrumentação e controle, para o dado momento, nos basta saber que os sinais relacionados a eventos físicos podem ser representados no domínio elétrico. Como os sinais elétricos são gerados a partir de eventos físicos, eles possuem um comportamento variável com o tempo, ou seja, a magnitude do sinal pode mudar de valor ao longo do tempo. Desta forma um sinal elétrico pode ser representado por um gráfico temporal, como o ilustrado na Figura 4.1. Existem no entanto, diversos termos utilizados para descrever as características de um determinado sinal elétrico. Nas próximas seçaões esses termos serão melhor discutidos. Figura 4.1: Sinal elétrico arbitrário
4.1.1 Elementos de um sinal elétrico Como comentado, um sinal elétrico pode se apresentar de diversas formas, dependendo do evento que o criou e do processamento sobre ele realizado. Assim sendo, costuma-se definir alguns parâmetros para melhor definir as características de cada sinal. Um sinal convencional possui três componentes básicos: • Amplitude - Define a magnitude do sinal elétrico (Unidade dependente do tipo de grandeza analisada); • Frequência - Define o número de ciclos que aquele sinal exibe em um segundo (Medido em Hertz); • Fase - Define o deslocamento do sinal em relação a um instante de referência (Medido em graus ou radianos); Um sinal pode, portanto, transportar informaçaões inseridas em pelo menos um desses três componentes. Existem, contudo diversas formas de se interpretar e trabalhar com cada um desses componentes, como será discutido mais a seguir. Para tanto, considere como exemplo inicial a representação de um sinal simples descrito na Figura 4.2. 4.1.1.1 Amplitude de um sinal A amplitude de um sinal elétrico mede a magnitude daquele sinal, sendo que a unidade referente a tal magnitude está relacionada àa grandeza analisada. Por exemplo, um sinal de tensão terá sua magnitude medida em Volts, um sinal de corrente, em Ampéres e um sinal potência, em Watts. A amplitude pode ser definida de várias formas diferentes, determinando valores distintos. Assim sendo, apresentamos aqui algumas definiçaões mais comumente utilizadas. 4.1.1.1.1 Valor Instantâneo O valor instantâneo de um sinal representa a magnitude do sinal em cada instante de tempo. Figura 4.2: Elementos de um sinal elétrico 4.1.1.1.2 Valor de pico-a-pico O Valor de pico-a-pico representa a magnitude existente entre o ponto máximo do sinal em um período e o seu ponto mínimo. Na Figura 4.2 o valor de pico-a-pico é representado por APP . 4.1.1.1.3 Valor de pico O valor de pico representa a magnitude existente entre o ponto máximo do sinal em um período e o valor médio do sinal. Na Figura, o valor de pico é representado por AP . 4.1.1.1.4 Valor médio O valor médio é a magnitude da média de um sinal ao longo de um período. Na Figura 4.2, o valor médio é representado por Am. A definição de valor médio é dada pela equação abaixo: Am = 1 T ∫ t 0 x(t)dt (4.1) Ou seja, �e igual �a soma das �areas sob a curva de um sinal, dividido pelo per��odo. 4.1.1.1.5 Valor E�caz ou RMS - Root Mean Square O valor RMS, ou seja , o valor médio quadrático, é um representação de magnitude muito utilizado em sistemas elétricos. Contudo esse valor não pode ser extraído apenas pela análise da forma de onda do sinal, como é feito com os demais. Esse valor surge com a necessidade de se medir a capacidade de gerar potência de um sinal. O valor eficaz é um valor cont��nuo atribuído a um sinal arbitrário, de modo que a potência dissipada sobre um resistor alimentado por um sinal contínuo de magnitude igual ao valor RMS de um sinal arbitrário será igual àa potência dissipada pelo mesmo resistor quando este é alimentado pelo sinal arbitrário em si. A equação que define o valor eficaz é: ARMS = √ 1 T ∫ t 0 x(t)2dt (4.2) Talvez o valor RMS mais importante de ser lembrado por alunos de eletrônica é o Valor Eficaz de uma senóide pura. Considera-se uma senóide pura um sinal elétrico de forma de onda senoidal com valor médio nulo e frequência fixa, como ilustra a Figura 4.3.Figura 4.3: Sinal senoidal puro Neste caso, o Valor Eficaz do sinal senoidal puro seria: ARMS;Senoide = A√P 2 (4.3) 4.1.1.2 Frequência de um sinal A frequência de um sinal elétrico representa quantos ciclos, ou períodos, daquele sinal ocorrem em um intervalo de um segundo. O valor de frequência é representado pela unidade Hertz (Hz), a qual significa ciclos/segundo. O valor inverso da frequência é o período de um sinal, ou seja, o tempo necessário para que este sinal complete um ciclo. Na Figura 4.2, o período do sinal é representado por T. Assim a frequência do sinal seria: f = 1 T (4.4) 4.1.1.3 Fase de um sinal Matematicamente, considera-se que um sinal periódico, seja ele elétrico ou não, tem duração eterna, ou seja, começaou em um tempo infinitamente distante e continuará parasempre mantendo os mesmos atributos que o descrevem. Sabemos que essa afirmação não é realista, uma vez que os sinais, como representaçaões de eventos físicos, duram um intervalo mensurável de tempo (mesmo que este seja de alguns milhões de anos!), no entanto, essa é uma maneira de podermos tratá-los como sinais periódicos e lançaar mão de ferramentas matemáticas conhecidas e simplificadas para analisá-los. Uma vez dito isso, fica claro que ao se analisar um período, ou trecho, de um sinal, é importante definir um instante de tempo de referência, ou seja, em qual momento queremos verificar os atributos de um determinado sinal. Acontece, todavia, que esse instante de referência não necessariamente estará alinhado com o início de um ciclo do sinal a ser analisado. àA distância (em radianos ou graus) entre o instante de referência e o início de um novo ciclo do sinal analisado dá-se o nome de ângulo de fase, ou simplesmente fase. Para exemplificar essa ideia, observe as duas ondas senoidais apresentadas na Figura 4.4. Figura 4.4: Ondas senoidais defasadas entre si. Note que a onda em Azul se inicia no mesmo instante em que o eixo do tempo tem seu valor nulo, ou seja, t = t0 = 0 (t0 normalmente é o símbolo utilizado para definir o instante de referência.). Nesse caso, dizemos que a onda senoidal possui fase nula, ou zero, pois está em fase com o instante de referência. Já a onda em Preto se inicia em um instante posterior ao da onda azul, sendo que a distância angular entre a onda preta e o instante t0 é de � 2 , ou 90o. Logo, podemos dizer que esta onda possui um ângulo de fase de 90o. Comumente podemos empregar o conceito de fase ao comparar duas ondas em um mesmo intervalo de tempo. Mantendo ainda o exemplo da Figura 4.4, podemos dizer que a onda preta está 90o atrasada em relação àa onda azul, isso pois a onda azul tem seu início em um instante anterior àa onda preta. Logo, existe um defasamento entre as duas ondas, o qual pode ser medido em graus (90o), ou radianos (� 2 ). No caso do sinal senoidal e seus derivados, a fase pode ser incorporada àa equação que define o sinal, como é mostrado a seguir: S(t) = Apsen(ωt + ϕ) (4.5)Onde: S(t) é o sinal dependente do tempo; Ap é o valor de pico do sinal; ω = 2πf é a frequência angular do sinal, medida em radianos/s; f é a frequência do sinal em Hertz; ϕ é o ângulo de fase em radianos; t é o instante de tempo que define um valor instantâneo do sinal avaliado; Exerc��cios Resolvidos 1 - Para o sinal mostrado na �gura 4.5 abaixo calcule: a) Valor de pico-a-pico; b) Valor médio; c) Valor de pico; d) Frequência (Hz); e) ângulo de fase. Figura 4.5: Forma de onda do exerc��cio E1.1. Resolu�c~ao: O sinal triangular mostrado na figura 4.5 excursiona entre os valores 0 e 4V, logo, o seu valor de pico-a-pico (diferençaa entre ponto máximo e mínimo) é de 4V. Para calcular o valor médio, deve-se calcular a área de um ciclo e dividi-la pelo período. Como a forma de onda é triangular, podemos utilizar a área de um triângulo [ Base × Altura 2 ] para calcular o que desejamos. Assim: Sarea = 4 · 6 × 103 ÷ 2 = 12 × 103V s. Como o período mostrado é de 6ms, o valor médio do sinal seria:  ̄ S = 12 × 103 6 × 103 = 2V .O valor de pico é a diferençaa entre o ponto de máximo do sinal (4V) e o seu valor médio (2V), assim, o valor de pico para o sinal em questão seria de: Sp = 4V − 2V = 2V . O sinal possui período igual a 6ms, como a frequência de um sinal é f = 1 T , a frequência do sinal será de: f = 1 6 × 103 = 166, 67Hz. Note que o primeiro ciclo do sinal após a origem do gráfico se inicia no instante t = 2ms, este intervalo de tempo corresponde àa defasagem do sinal em relação àa origem. Contudo, como foi pedido o ângulo de defasagem, devemos realizar uma regra de três para definir a resposta correta. Lembrando que um ciclo completo corresponde a uma volta completa no círculo trigonométrico, ou seja, 360o ou 2π radianos, fazemos: 2ms 6ms = ϕ 360o ϕ = 2ms 6ms · 360o = 360o 3
120o
2π 3 rad. Resp. a) 4V; b) 2V; c) 2V; d) 166,67Hz; e) 120o ou 2� 3 rad.4.2 Circuitos com entrada c.a. Muitas vezes, um circuito a diodos é alimentado por um sinal alternado. Para se realizar a análise do sistema, deve-se verificar o comportamento para diversas possibilidades de funcionamento, ou seja, deve-se procurar por pontos de operação do circuito. Como exemplo, tome o circuito a diodos da Figura 4.9.
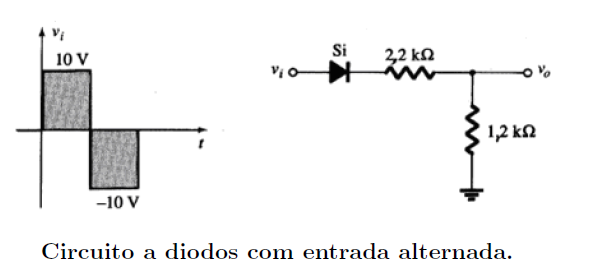
Figura 4.8: Circuito a diodos com entrada alternada. Neste circuito existem duas condiçaões de operação: • Quando a tensão de entrada é positiva; • Quando a tensão de entrada é negativa. Quando a tensão vi é positiva, note que o diodo estará diretamente polarizado, de modo que o circuito se torna:
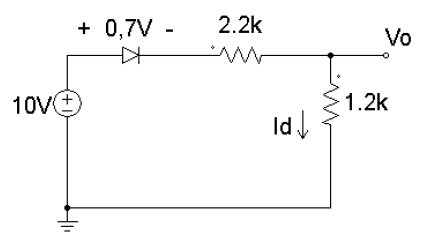
Figura 4.9: Circuito a diodos com tens~ao de entrada positiva. Neste caso, pode-se escrever que: 10V = 0, 7V + (2, 2kΩ + 1, 2kΩ) · ID (4.6) De modo que a corrente na malha se torne: ID = 10V − 0, 7V 2, 2kΩ + 1, 2kΩ = 2, 73mA (4.7) A tensão de saída será então:Vo = 1, 2kΩ · ID = 3, 28V (4.8) No segundo caso, quando a tensão se tornar negativa, o diodo estará reversamente polarizado. Isso faz com que ele bloqueie a circulação de corrente, como ilustra a Figura 4.10.
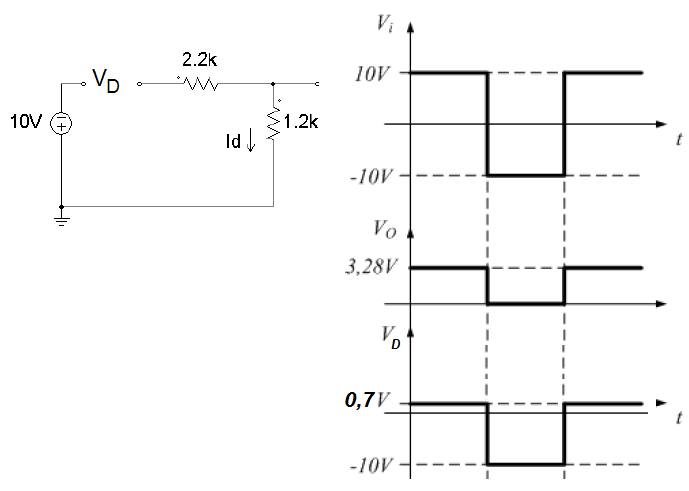
Figura 4.10: Circuito a diodos com tens~ao de entrada negativa. Neste caso, como não há circulação de corrente, a tensão Vo = 0V . Com essas informa çaões, pode-se esboçaar a forma de onda de tensão na saída, levando em consideração as análises feitas. A Figura 4.11 apresenta as formas de onda de tensão na entrada e na saída do circuito.
Figura 4.11: Formas de onda de tens~ao na entrada e na sa��da do circuito com entrada c.a..
Nota-se que a análise de circuitos com entrada c.a. pode se tornar bastante complexa,
dependendo da montagem e da forma de onda do sinal alternado. Para simplificar o estudo
dessas montagens, podemos determinar circuitos básicos a diodos, os quais podem
ser encontrados em diversas aplicaçaões. Nesta apostila abordaremos dois desses circuitos,
os retificadores (como o exemplo dado acima) e os limitadores (ceifadores). Outros circuitos
básicos, como os dobradores de tensão e grampeadores, podem ser encontrados nas
referências desta apostila.4.2.1 Limitadores de tens~ao
Os circuitos limitadores, também denominados ceifadores, são projetados para limitar
o nível de tensão em sua saída. A aplicação principal dessa montagem é proteger outros
circuitos de sobre-tensões provocadas por falhas nos circuitos, curto-circuito, ou ruídos
induzidos, no entanto, existem aplicaçaões onde o ceifamento é feito propositalmente, como
no caso de distorcedores de áudio e geradores de forma de onda. A montagem básica de
um limitador é apresentada na Figura 4.12.
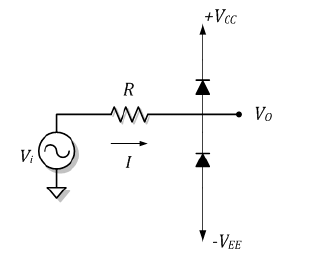
Figura 4.12: Circuito b�asico de um limitador de tens~ao. Observe que os diodos são conectados entre a saída do circuito e duas tensões contínuas, uma positiva (+VCC) e outra negativa (−VEE). Esses diodos apenas conduzirão em duas condiçaões: • Tensão de saída igual a +VCC + 0, 7V ; • Tensão de saída igual a −VEE − 0, 7V . Em qualquer outra situação os diodos se encontrarão em corte. Como a tensão de entrada é conectada àa saída por meio de um resistor, e este apenas perceberá corrente quando os diodos estiverem em condução, quando os diodos estiverem em corte a tensão de saída será sempre igual àa tensão de entrada. Com isso se percebe a finalidade do circuito: Enquanto a tensão de entrada estiver entre os limites comentados acima, ela passará pelo circuito limitador sem alteração. Quando a tensão de entrada extrapolar os limites, ela será limitada pelos diodos. Como exemplo, tome a seguinte condição: VCC = 15V , VEE = 10V . Assumiremos uma tensão de entrada triangular (poderia ser qualquer forma) com valor de pico igual a 5V. A Figura 4.13 apresenta a forma de onda da tensão de entrada e os limites de condução dos diodos.
Note que como a tensão de entrada é inferior aos patamares de saturação (limites de
tensão na saída do circuito) os diodos não entrarão em condução e portanto, a tensão de
saída será igual àa tensão de entrada.
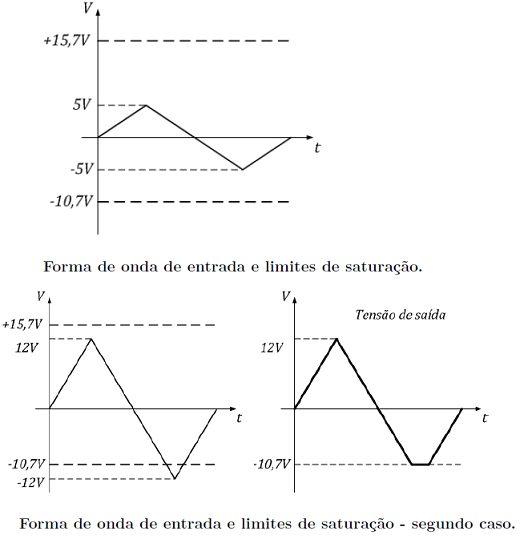
Caso o nível da tensão de entra seja elevada a 12V, ter-se-á as formas de onda
mostradas na Figura 4.14. Neste segundo caso, a tensão de entrada supera o limiteFigura 4.13: Forma de onda de entrada e limites de satura�c~ao.
inferior de saturação. Assim, o diodo inferior irá conduzir e limitar a tensão de saída,
durante o intervalo em que a tensão é inferior a -10,7V, àa tensão de saturação. Com isso,
nota-se que há uma deformação na forma de onda da tensão de saída, a qual é ceifada em
seu pico inferior. Caso a tensão de entrada se eleve ainda mais, ocorrerá o ceifamento no
pico superior também.
Figura 4.14: Forma de onda de entrada e limites de satura�c~ao - segundo caso.
O mesmo efeito pode ser obtido com um circuito a zeners, como o apresentado na
Figura 4.15. Os limites de saturação seriam determinados pelas tensões de avalanche dos
dispositivos. Neste exemplo, os limites de saturação seriam ±(VZ + 0, 7V ).
OBS: Pode-se variar os valores dos limites de saturação, ou se retirar diodos, de modo
a se ter apenas um limite de saturação. No entanto, o efeito de limitação sempre ocorrerá
quando houver algum dispositivo que impeçaa a elevação do nível de tensão acima de um
valor pré-determinado.
Figura 4.15: Circuito limitador a zeners.
4.2.2 Retificador Básico Os circuitos retificadores são utilizados em uma larga gama de aplicaçaões: conversores CA/CC, fontes de alimentação, detectores de valor de pico, geradores de forma de onda, etc. Na seção seguinte iremos verificar o funcionamento de retificadores aplicados a fontes de alimentação monofásicas. O objetivo principal de um retificador é eliminar alguma parcela do sinal de entrada, de modo que a saída exiba um nível médio diferente de zero. O circuito básico de um retificador é apresentado na Figura 4.16. Figura 4.16: Circuito b�asico de um reti�cador. Note que só existirá tensão na saída se o diodo conduzir e essa condição apenas será satisfeita se a tensão de entrada for positiva e superior àa tensão de limiar do diodo, ou seja, Vi ≥ 0, 7V . Com essa observação, podemos esboçaar a forma de onda de entrada e saída do circuito, consideraremos para tal uma tensão de entrada triangular de valor de pico 10V, como mostra a Figura 4.17. Figura 4.17: Formas de onda de um reti�cador b�asico. Observe que o diodo deixará passar para a saída apenas a parcela de tensão que é Prof. Thiagosuperior àa sua tensão de limiar, assim o valor de pico da tensão de saída é de Vimax−0, 7V , como no nosso exemplo a tensão de pico de entrada é de 10V, a tensão de pico da saída será de 9,3V.
| << Circuitos com diodos | AULA 4 - Circuitos Retificadores | >> |
|---|