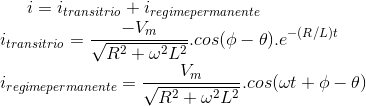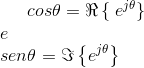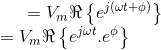AULA 3 - Circuitos 2 - Engenharia
<<< Voltar para página principal do curso
Resposta Senoidal em Regime Permanente
Já vimos que a geração dos sinais de energia elétrica é senoidal.
Mas qual será a resposta dos circuitos elétricos, a este tipo de alimentação????
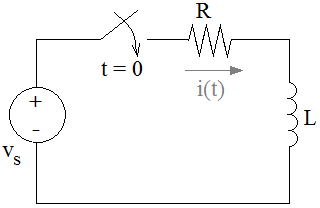
Seja o circuito CA abaixo, alimentado por uma tensão vs senoidal:
Admitindo também que a corrente inicial no circuito seja zero e tomando como referência de tempo, o instante em que a chave é fechada, a aplicação direta das Leis de Kirchoff ao circuito, resultará na equação diferencial ordinária abaixo:
cuja solução é dada por:
onde θ é o ângulo cuja tangente é ωL/R
Em tempo, o aluno vai aprender a analisar o comportamento dos componentes indutor (L) e capacitor (C) em circuitos elétricos, vai aprender a resolver equações diferenciais ordinárias (EDO's) e, principalmente, a analisar e compreender o comportamento de um circuito elétrico, no que se conhece por transitório.
Por ora, basta que o aluno entenda que a equação acima é composta de duas partes: o termo da direita, que se refere à resposta transitória, e o termo que se refere ao regime permanente, no circuito:
O termo de componente transitório da corrente é assim chamado porque ele torna-se infinitesimal, praticamente nulo, à medida que o tempo passa.
O estudo do comportamento transitório, ou transiente, em um circuito elétrico é interessante na determinação dos comportamentos deste, em caso de desligamento/religamento e faltas.
Já o regime permanente pode ser visto como o comportamento a longo prazo, de acomodação de um circuito. Isto é, depois de um certo período de tempo que a chave do circuito foi fechada (função da exponencial natural elevada a -R/L), o circuito poderá ser descrito apenas pelo termo da direita, o de regime permanente!!!
O termo referente ao regime permanente, na equação acima, nos traz algumas conclusões:
- A solução de regime permanente é uma função senoidal, assim como a tensão de alimentação vs;
- A frequência do sinal de resposta é idêntica à frequência do sinal da fonte. Essa condição é sempre verdadeira em circuitos lineares invariantes;
- Em geral, a amplitude máxima da resposta de regime permanente é diferente da amplitude máxima da fonte;
- Em geral, o ângulo de fase do sinal de resposta é diferente do ângulo de fase da fonte.
É importante pontuar que estas informações de amplitude e fase são dependentes dos componentes do circuito e são, justamente, o que se tenta determinar, para conhecer a resposta em regime permanente de um circuito!!!
Fasores
Já sabemos que a forma de onda dos sinais de alimentação de tensão e corrente são senoidais.
Porém, funções senoidais são difíceis de manipular matematicamente, pois exigem que se conheça não poucas relações trigonométricas...
A pergunta é: existiria uma função matemática equivalente às senóides/cossenóides que permitisse a realização dos cálculos matemáticos de corrente e tensão alternados, SEM que se tivesse que utilizar as relações trigonométricas???
Felizmente, a resposta é SIM! :)
Os fasores são números complexos, baseados na função exponencial, que são associados às tensões e correntes senoidais, de forma a permitir cálculos matemáticos simplificados!!!
Em outras palavras, FASOR é um número complexo que contém as informações de amplitude e ângulo de fase de uma função senoidal.
O conceito de fasor é fundamentado na identidade de Euler, que relaciona a função exponencial com a função trigonométrica:
Podemos considerar a função cosseno como parte real da função exponencial e a função seno, como parte imaginária, isto é:
O sinal de alimentação v = Vm. cos(ωt + φ) pode ser descrito como:
ou:
Onde a quantidade 
é um número complexo que contém a informação sobre a amplitude e o ângulo de fase da função senoidal dada.
Da mesma forma, a resposta de corrente do circuito RL vai ser:
que pode ser escrita como:
É fácil observar que o fator complexo 
permanece sempre inalterado, em todos os cálculos.
De fato, em circuitos nos quais a fonte é alimentada por tensão senoidal de velocidade angular constante ω, este termo também é constante.
Assim, a tensão senoidal pode ser representada apenas por:
e a corrente, por:
onde V e I são números complexos que representam a amplitude e a fase de uma senóide.
Esses números complexos são, por definição, FASORES, ou representações fasoriais, das senoidais dadas.
O fasor pode ser escrito na forma exponencial, na forma polar, ou na forma retangular.
Para uma revisão acerca de números complexos, consulte: Operações com números complexos Conversão entre formas polar e retangular
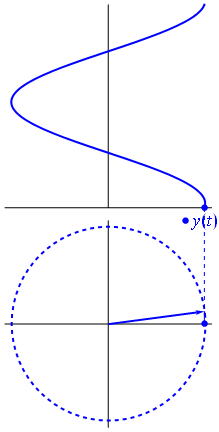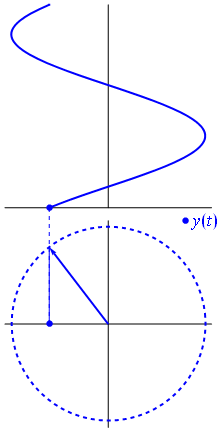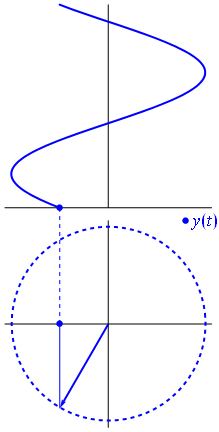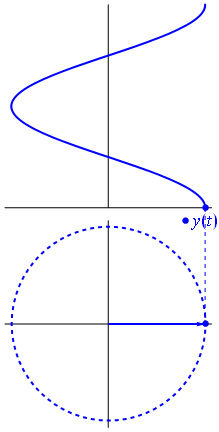
O fasor pode ser também visto como um vetor radial girante, com a mesma frequência da senóide:
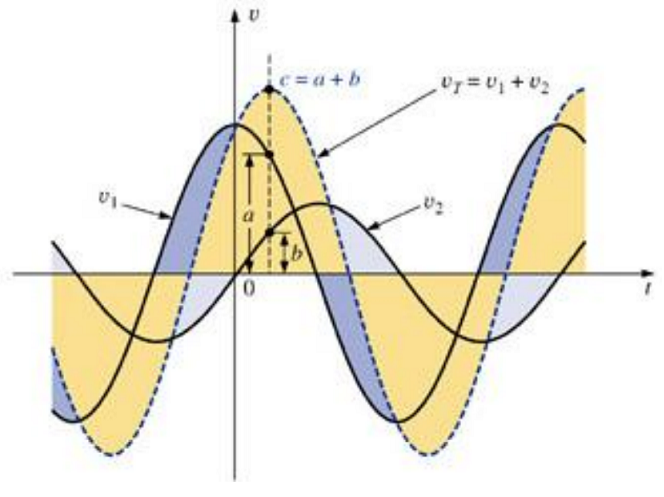
Já a soma de senóides representadas fasorialmente pode ser feita como soma simples de números complexos.
Por exemplo:
As senóides v1 e v2 podem ser descritas, respectivamente por:
ou
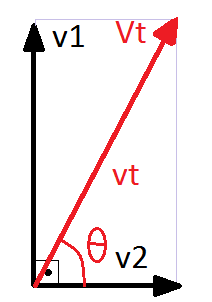
e a tensão total vt, resultante da soma de v1 e v2, vai ser dada por:
Exemplo:
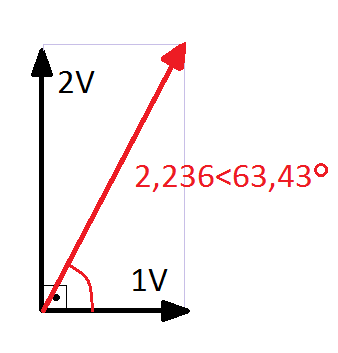
Calcule o fasor vt = v1 + v2, onde v1 = 2<90º [V] e v2 = 1<0º [V].
vt = {2.cos(90º) + 1.cos(0º)} + j.{2.sen(90º) + 1.sen(0º)}
vt = {2.0 + 1.1} + j.{2.1 + 1.0}
vt = 1 + j.2
Na forma polar:
Vt = (1.1 + 2.2)½ = 2,236 [V]
e
θ = arc tg(2/1) = 63,43º ou 1,107 rad.
Exercícios:
Seção 14.12, pg. 441, Boylestad.
| << Valor médio e eficaz | AULA 3 - Geração em corrente alternada - Fasores | Reatâncias e Impedâncias >> |
|---|