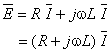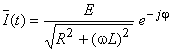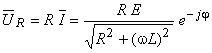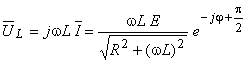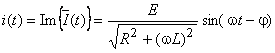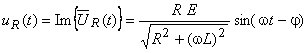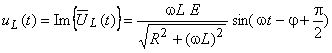AULA 5 - Circuitos 2 - Engenharia
<<< Voltar para página principal do curso
Resposta em Regime Senoidal para circuitos RL
Um circuito resistor-indutor (circuito RL), filtro RL ou malha RL, é um tipos mais simples de filtros eletrônicos analógicos.
Ele consiste de um resistor e de um indutor, podendo estar ligados tanto em série quanto em paralelo, sendo normalmente alimentados por uma fonte de tensão.
Existem três componentes básicos destes circuitos analógicos: o resistor (R), o capacitor (C) e o indutor (L).
Estes podem ser combinados em quatro importantes circuitos:
- o circuito RC,
- o circuito RL,
- o circuito LC
- e o circuito RLC.
Estes circuitos, entre eles, exibem um grande número de tipos de comportamentos que são fundamentais em grande parte da eletrônica analógica.
Em particular, eles são capazes de atuar como filtros passivos. Este artigo considera o circuito RL, em ambas as ligações paralela e série, como mostrado nos diagramas.
Circuito RL Série
(Modificado de: e-Learning Tools for Electrical Engineering)
A seguir discutiremos o comportamento de um circuito elétrico contendo dois elementos: um resistor e um indutor, como mostra a Fig. 1.
Os resistores têm como característica principal a transformação de energia elétrica em energia térmica, já os indutores transformam energia elétrica em energia magnética.
Figura 1 – Circuito RL série
Considere-se o circuito RL série alimentado por uma fonte de tensão alternada sinusoidal cuja tensão é descrita pela expressão e(t) = E.sen(ωt).
Figura 2 – Esquema do circuito RL série com fonte senoidal
Conhecidos os valores de R e L, pretende determinar-se o regime permanente da evolução temporal da corrente no circuito, i(t), e das tensões aos terminais da resistência, ![]() , e da indutância,
, e da indutância, ![]() .
.
Através da Lei das Malhas, a soma da tensão nos terminais da resistência e nos terminais da bobina, será igual à tensão da fonte:
Em termos de amplitudes complexas a expressão anterior escreve-se:
onde R + j.ωL representa a impedância complexa do circuito, isto é, da resistência em série com a indutância.
Explicitando ![]() na expressão anterior, obtém-se:
na expressão anterior, obtém-se:
com φ = arc tan (ωL)/R e 0 < φ < π/2.
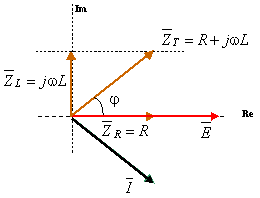
O diagrama fasorial da impedância, e amplitudes complexas da tensão da fonte e corrente, estão representados na figura abaixo.
Figura 3 – Diagrama fasorial das impedâncias
Note que a impedância complexa total é a soma vetorial dos fasores de resistência e da reatância indutiva.
Uma vez determinada a corrente, o cálculo da tensão no resistor é dado por:
que está em fase com a corrente.
Já a tensão nos terminais do indutor é:
A tensão complexa ![]() está avançada 90°, ou π/2 com relação a
está avançada 90°, ou π/2 com relação a ![]() à corrente que a percorre.
à corrente que a percorre.
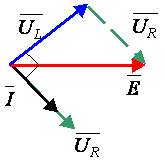
O diagrama fasorial completo das tensões e correntes do circuito, encontra-se representado na figura abaixo, onde se evidenciou a Lei das Malhas: a soma dos fasores ![]() e
e ![]() , os quais se igualam ao fasor da fonte
, os quais se igualam ao fasor da fonte ![]() .
.
Figura 4 – Diagrama fasorial das tensões e correntes do circuito RL
As expressões temporais para a corrente e tensões são dadas por:
,
e
com φ = arc tan (ωL)/R e 0 < φ < π/2.
As expressões que foram deduzidas admitiram que a tensão que alimenta o circuito tem uma fase inicial nula.
Porém, os diagramas fasorial e temporal que se obtêm são perfeitamente equivalentes aos obtidos quando se considera a tensão de alimentação com fase inicial nula; apenas diferem no instante a que se referem.
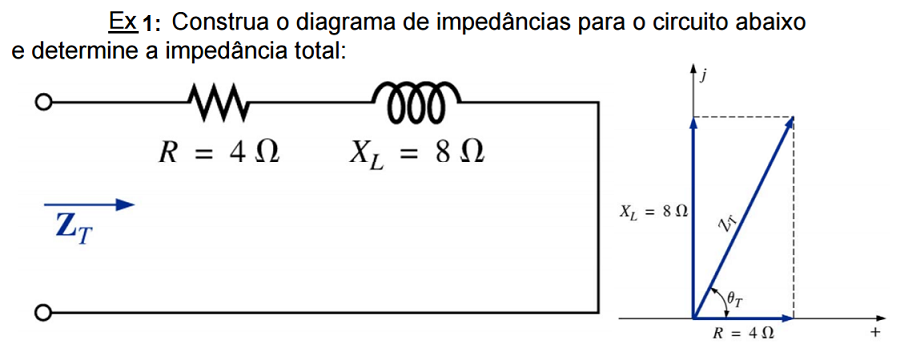
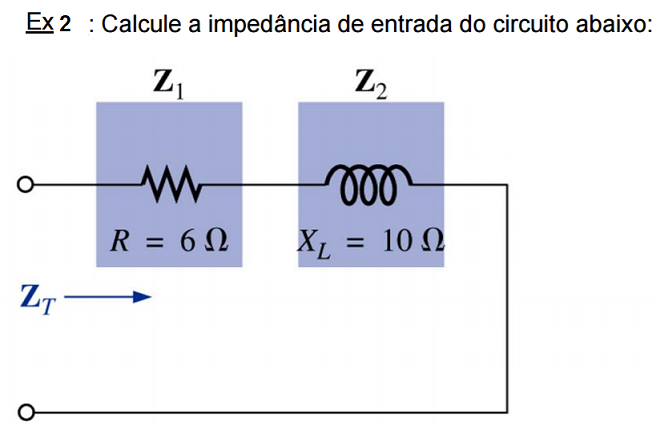
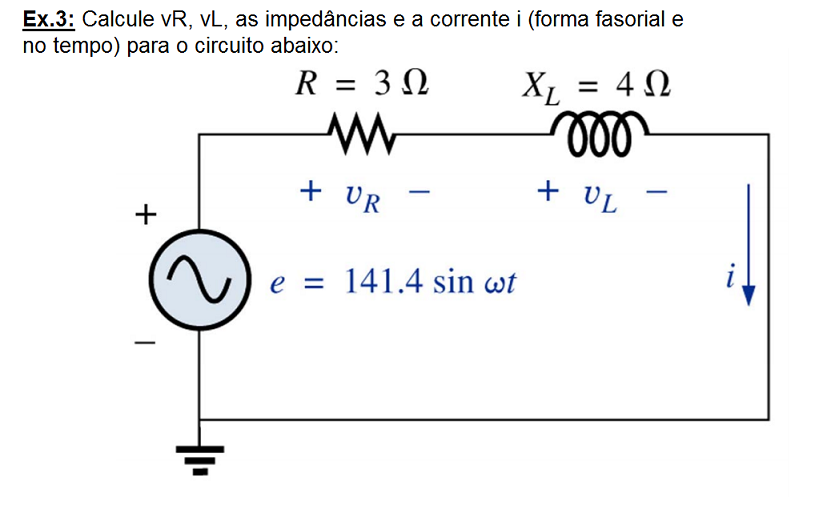
Exercícios
| << Impedância e Reatâncias | AULA 5 - Circuitos RL | Circuitos RC >> |
|---|