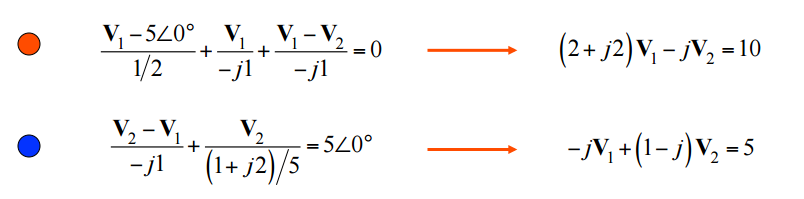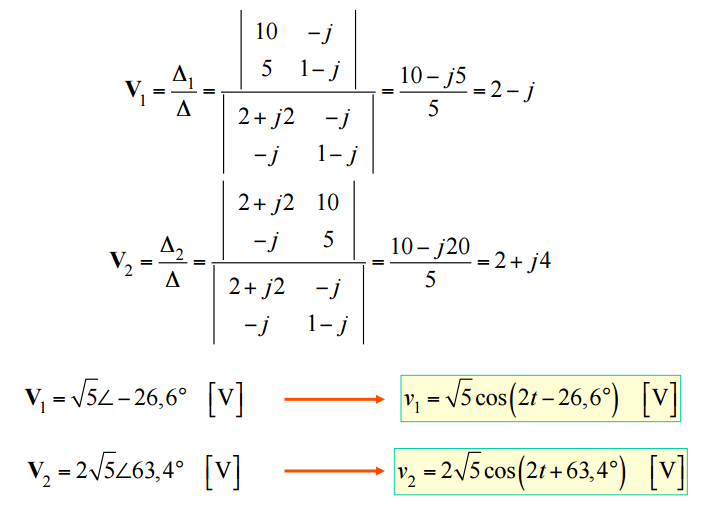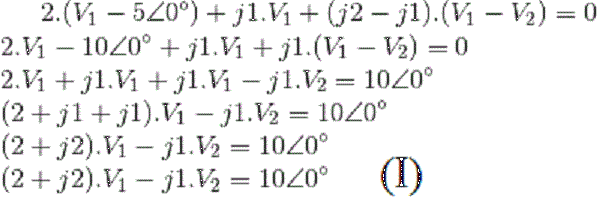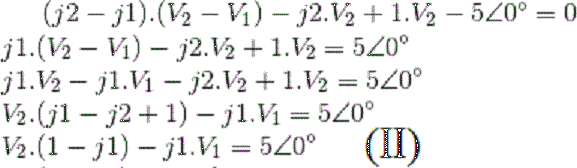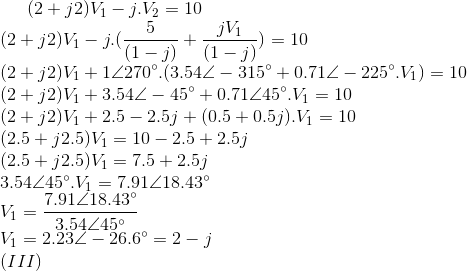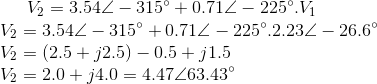AULA 9 - Circuitos 2 - Engenharia
<<< Voltar para página principal do curso
Análise de circuitos CA em regime permanente
Baseado no curso de Circuitos Elétricos I, Prof. Renato Baldini Fo., do Departamento de Comunicações Faculdade de Engenharia Elétrica e de Computação, Universidade Estadual de Campinas. Disponível em: [http://www.decom.fee.unicamp.br/~baldini/EA513.htm]
Análise Nodal
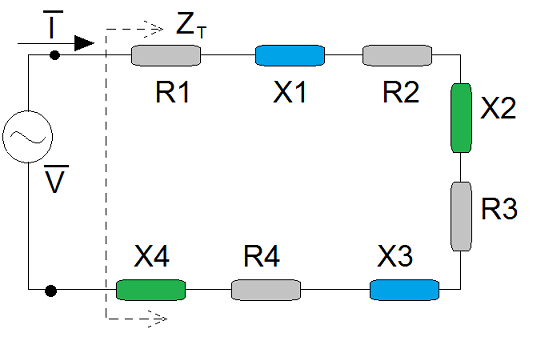
Seja o circuito série abaixo.
A Relação tensão-corrente será dada por:
onde Zt é a impedância total do circuito série, vista através dos terminais da fonte, isto é:
Assim, a diferença entre circuitos resistivos e fasoriais, é que no segundo, tanto as excitações quanto as respostas são complexas.
Os próximos exemplos comprovam que os métodos de análise nodal e de malhas também podem ser utilizados em circuitos fasoriais.
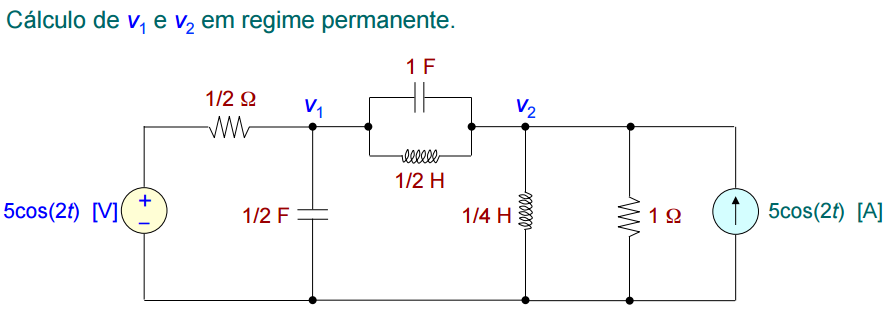
Exemplo 1:
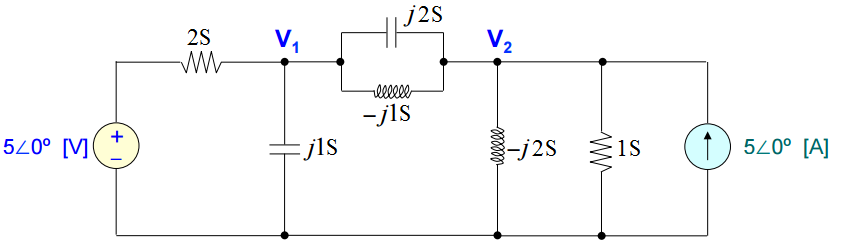
Seja o circuito acima, alimentado por sinal cossenoidal com ω = 2.
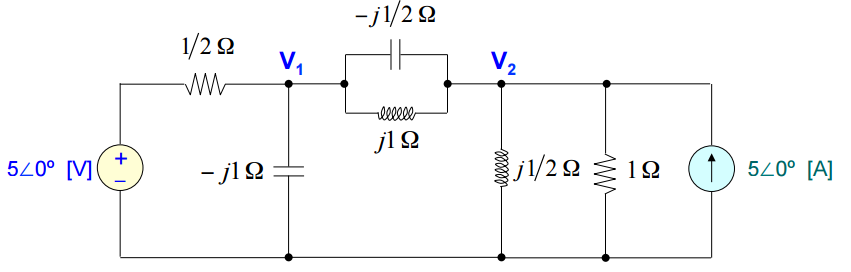
Na forma fasorial, o circuito será reescrito como:
onde:
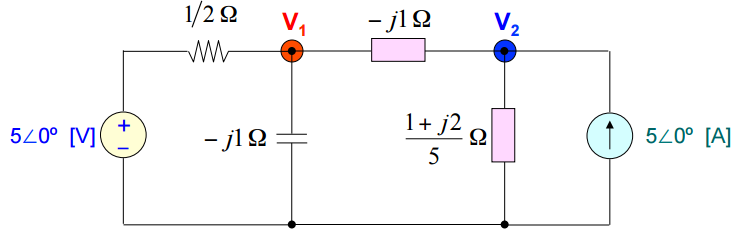
Assim como seria feito num circuito puramente resistivo, pode-se simplificar o circuito calculando as impedâncias equivalentes dos paralelos:
Também como é feito em circuitos resistivos puros, arbitra-se tensões em cada um dos nós e faz-se o somatório das correntes nestes nós, na forma V/Z, quais sejam:
e resolve-se estas equações.
A solução através de determinantes seria:
Assim como na análise resistiva, uma melhor abordagem seria resolver o circuito por meio de suas admitâncias Y = 1/Z.
As equações nodais para soma de correntes tornam-se da forma Y.V:
e
Portanto, substituindo-se I em II:
Agora, calculando V2, pela substituição de (III) em (II):
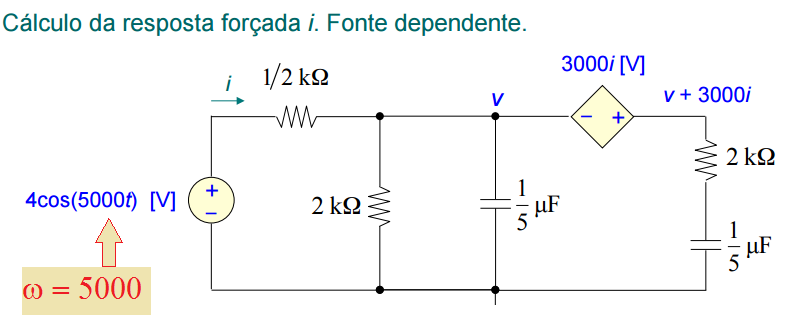
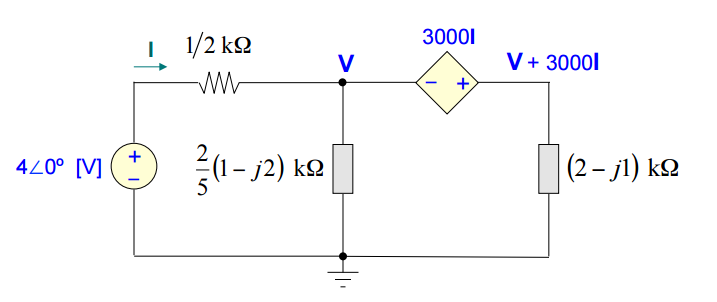
Exemplo 2:
Na forma fasorial e já simplificado com as impedâncias resultantes dos paralelos, o circuito será reescrito como:
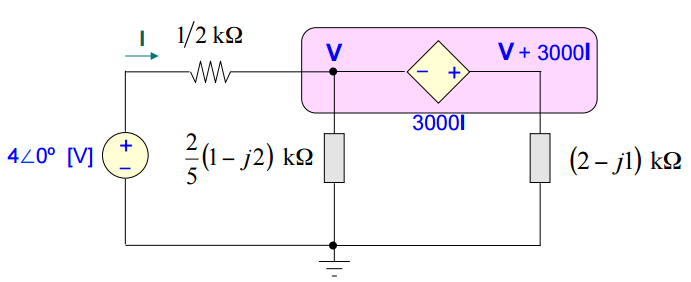
Assim como seria feito num circuito puramente resistivo, substitui-se a fonte dependente por um super-nó:
as equações nodais e a solução serão:
Análise de Malhas
Assim como num circuito resistivo puro, a análise de malhas pode ser aplicada em um circuito fasorial, simplesmente substituindo as indutâncias e capacitâncias por reatâncias e as tensões e correntes senoidais, por seus respectivos fasores.
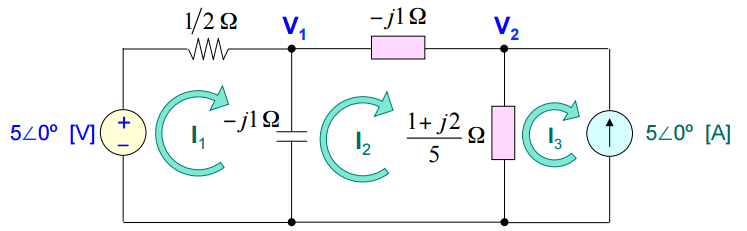
Exemplo 3:
Seja o circuito abaixo:
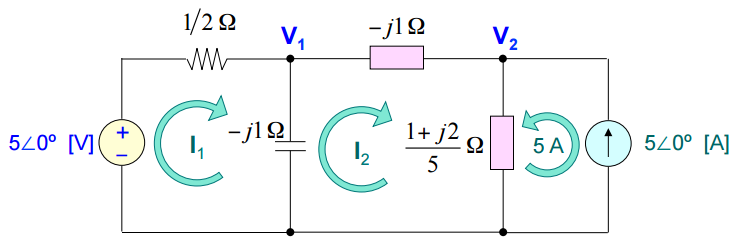
Arbitra-se as correntes I1, I2 e I3 nas malhas:
A corrente na terceira malha será dada pelo valor da fonte de corrente de 5A.
As equações das tensões nas malhas, da forma Z.I serão dadas por:
e
Substituindo:
| << Circuitos RLC | Análise CA em regime permanente | Potência CA >> |
|---|