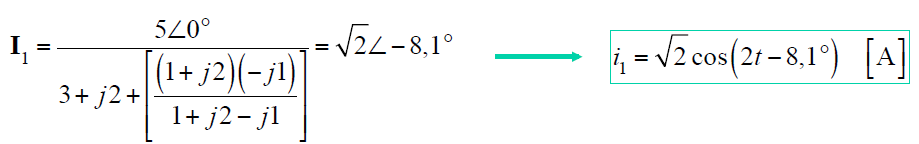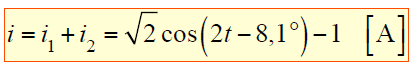AULA 10 - Circuitos 2 - Engenharia
<<< Voltar para página principal do curso
Teoremas de Rede em circuitos CA em regime permanente
Para regime permanente senoidal, analisado por fasores, valem as mesmas regras de análise utilizadas circuitos resistivos, pois as leis de Kirchhoff continuam sendo aplicadas. Assim sendo são válidas as mesmas considerações sobre linearidade e invariância com o tempo, o que inclui os teoremas de superposição, Thèvenin e Norton bem como associações de componentes e simplificações e, obviamente, os métodos de análise por correntes de malha e tensões de nó.
Baseado no curso de Circuitos Elétricos I, Prof. Renato Baldini Fo., do Departamento de Comunicações Faculdade de Engenharia Elétrica e de Computação, Universidade Estadual de Campinas. Disponível em: [http://www.decom.fee.unicamp.br/~baldini/EA513.htm]
Superposição
Em circuitos lineares alimentados por corrente alternada, o princípio da superposição também pode ser aplicado, em regime permanente, substituindo-se as resistências por impedâncias, e as fontes, pelos seus respectivos fasores.
Para os casos de circuitos excitados com fontes senoidais, sejam elas de freqüências iguais ou diferentes, podemos utilizar o princípio da superposição para obter a resposta da variável de rede desejada.
Exemplo 1:
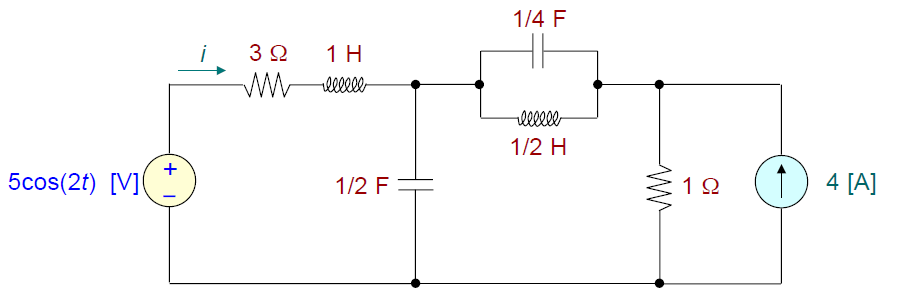
Calcule a resposta forçada para i:
A corrente i é composta pelas parcelas i1 e i2, a primeira devida à fonte de tensão alternada, e a segunda, devida à fonte de corrente contínua.
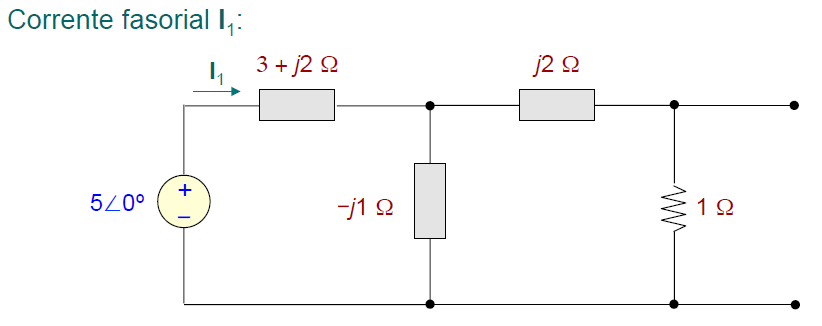
Assim, anulando-se a fonte de corrente:
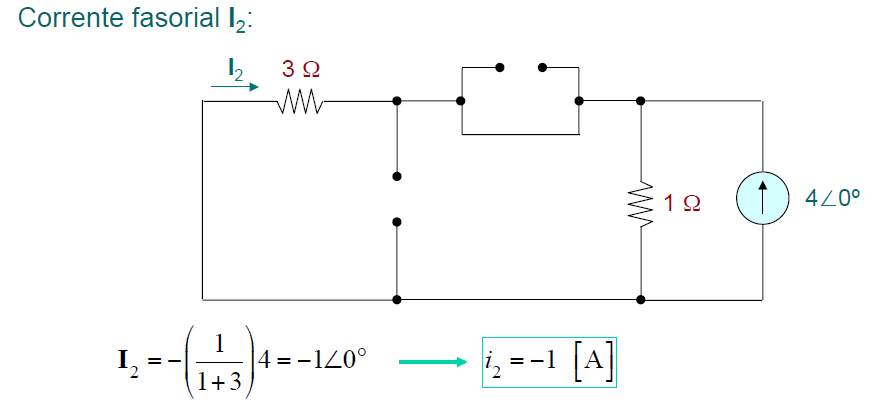
Agora, anulando-se a fonte de tensão (ω=0), também anula-se as impedâncias que dependem da frequência ω. O circuito fica:
E a resposta forçada para i será:
Exercícios
Resolva os circuitos abaixo pelo método de superposição:
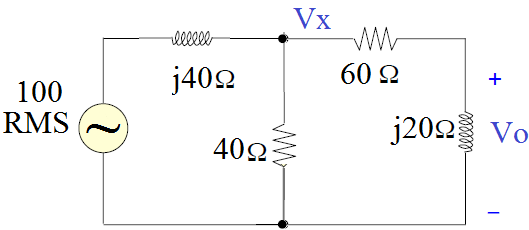
1) Calcule a tensão de saída Vo, no circuito CA em regime permanente abaixo:
Resposta: V0 = 15.8<18.43
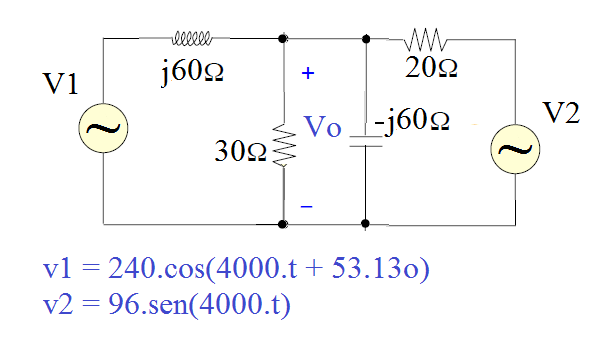
2) Calcule a tensão Vo, no circuito CA em regime permanente abaixo:
Resposta: Solução por superposição
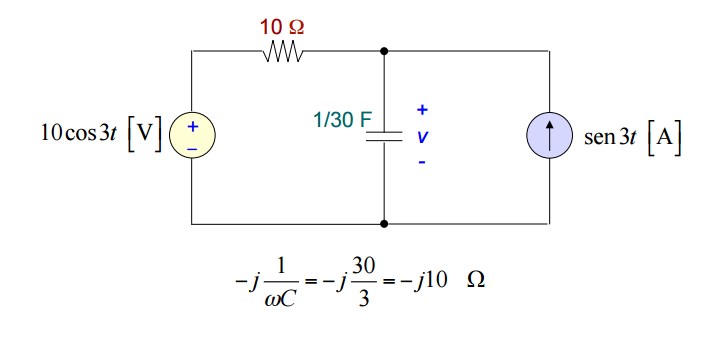
3)
Resposta: vf =10cos(3t −90°) =10sen(3t)
4)
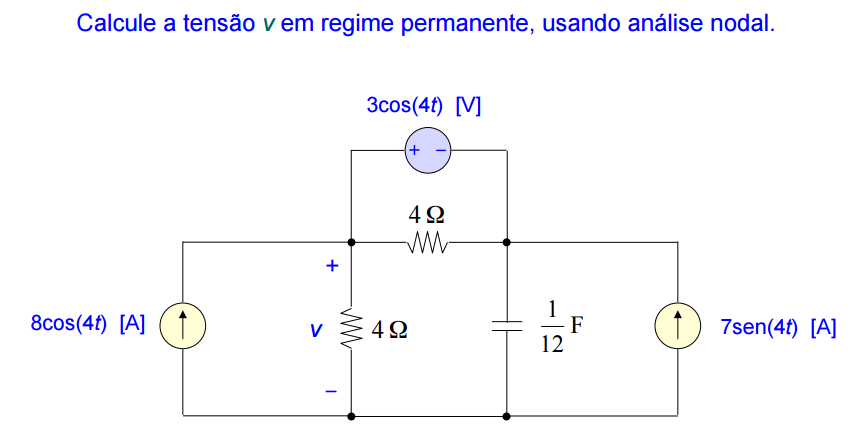
Resposta: v = = 24sen(4t) [V]
5)
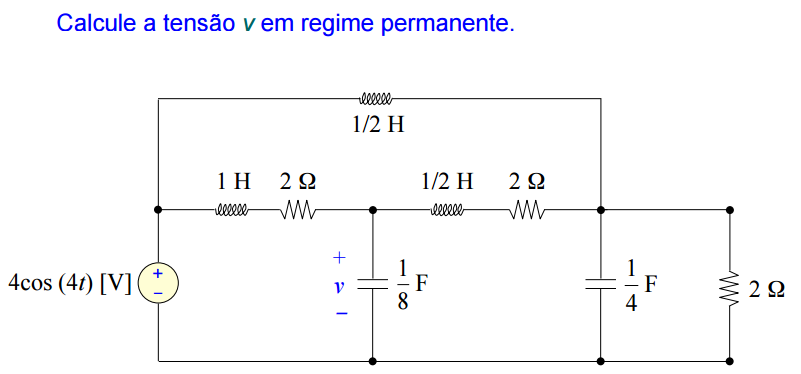
Resposta: v = 2.82. cos(4t −135º) [V]
Teorema de Thevenin
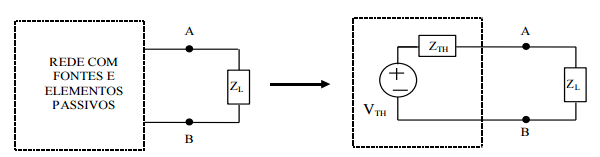
“Uma rede que contenha somente fontes de energia e elementos passivos pode se substituída por uma única fonte de tensão (VTH) em série com uma impedância (ZTH).”
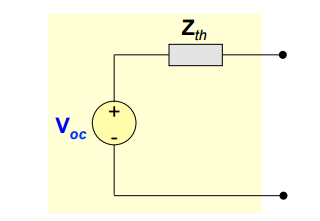
A tensão Vth é também denominada de tensão de circuito aberto (VOC – open-circuit), sendo definida como a tensão nos terminais AB com impedância ZL desconectada.
A impedância Zth é definida como a impedância de entrada vista a partir dos terminais AB com a rede INATIVA.
Por conseguinte, deve-se substituir todas as fontes por suas respectivas impedâncias internas.
O Equivalente de Thévenin pode ser construído a partir de duas etapas:
- Determinar a impedância de Thévenin, também chamada de impedância equivalente. Esta resistência (ou impedância) é aquela vista a partir dos terminais onde se deseja reduzir o circuito, e neste caso, com as fontes de tensão curto-circuitadas e as fontes de corrente abertas.
- Determinar a tensão de circuito aberto no ponto onde se deseja reduzir o circuito.
Deve haver uma única frequência (ω) presente, caso contrário devemos empregar superposição para dividir em problemas de frequências únicas, onde para cada circuito teremos um equivalente de Thévenin.
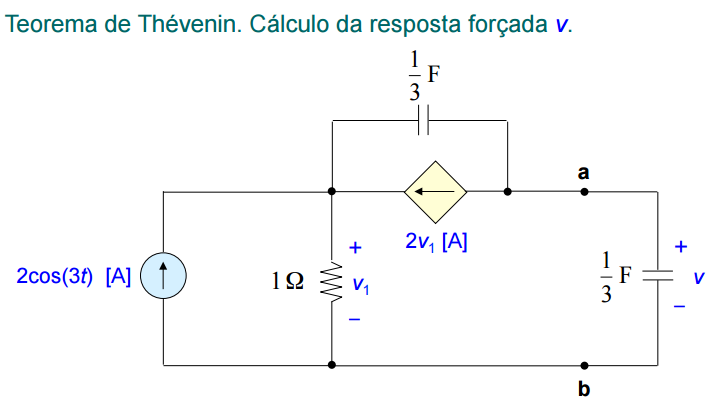
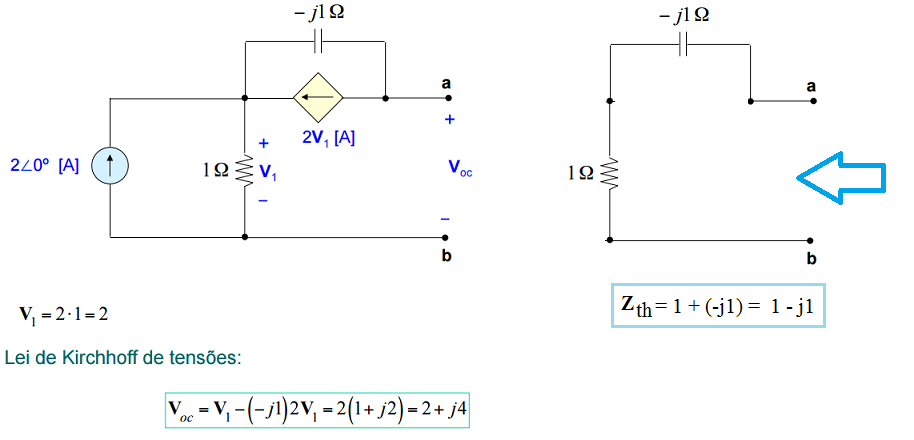
Exemplo:
Resolução:
Teorema de Norton
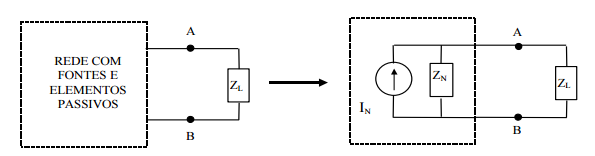
“Uma rede que contenha fonte de energia e elementos passivos pode ser substituída por uma única fonte de corrente (IN) em paralelo com uma impedância (ZN).”
A corrente IN é também denominada de corrente de curto-circuito (ISC - short-circuit), sendo definida como a corrente nos terminais AB com a impedância de carga ZL substituída por um curto-circuito.
Uma observação dos dois teoremas, citados acima, e a utilização dos conceitos de transformação de fontes implica que existe uma dualidade entre estes dois teoremas, sendo:
Zth = ZN
Vth = IN.ZN
IN = Vth/Zth
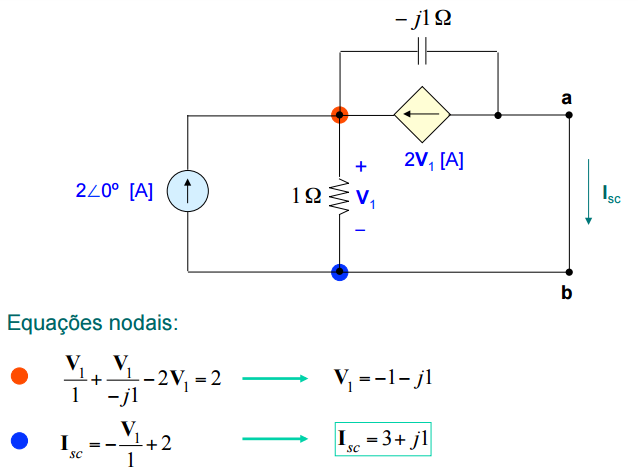
Exemplo:
Resolvendo o circuito anterior por Norton:
<<< Voltar para página principal do curso
| << Técnicas básicas de análise de circuitos CA em regime permanente | Análise CA em regime permanente | Potências CA >> |
|---|