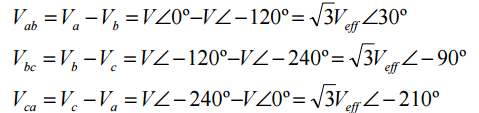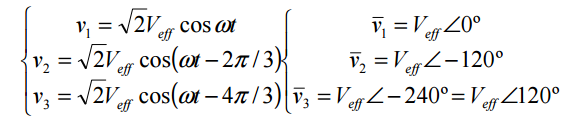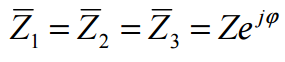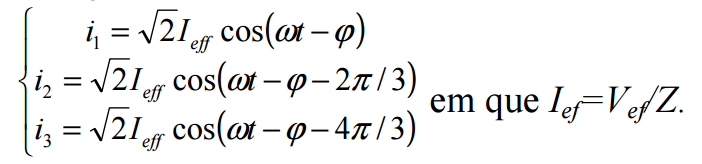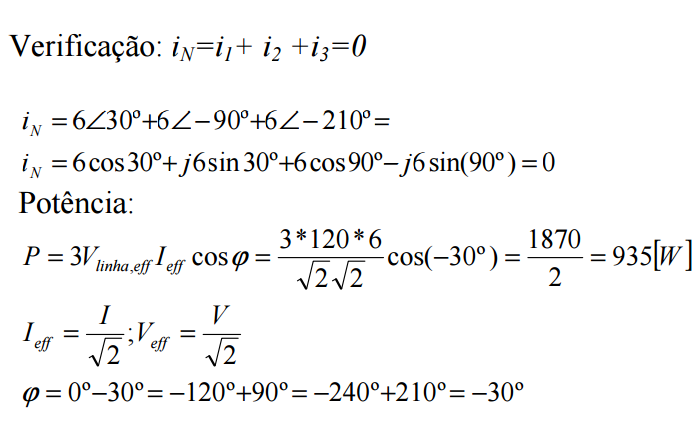AULA 15 - Circuitos 2 - Engenharia

Modificado de [1]

Circuitos Polifásicos

Enquanto num circuito monofásico existe apenas uma fonte de energia A.C. ou várias fontes fornecendo energia em fase à carga, nos circuitos polifásicos existem 2 ou mais fontes de tensão iguais com diferenças nas fases fixas, i.e., iguais em amplitude mas simétricas nas fases, fornecendo energia às cargas ligadas em linha.

A geração e transmissão de energia elétrica é mais eficiente em sistemas polifásicos que empregam combinações de 2, 3 ou mais tensões sinusoidais.

O sistema trifásico foi independentemente inventado por Galileo Ferraris, Mikhail Dolivo-Dobrovolski e Nikola Tesla nos meados do fim da década de 1880.

Circuito Trifásico Equilibrado

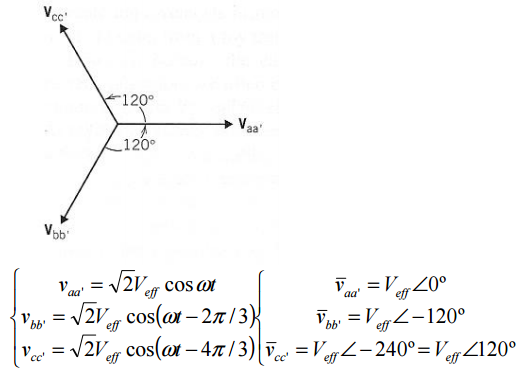
É constituído por 3 tensões sinusoidais possuindo amplitudes e frequências iguais, com desafamento de 120º entre si.

Vaa’ + Vbb’ + Vcc’ = 0 

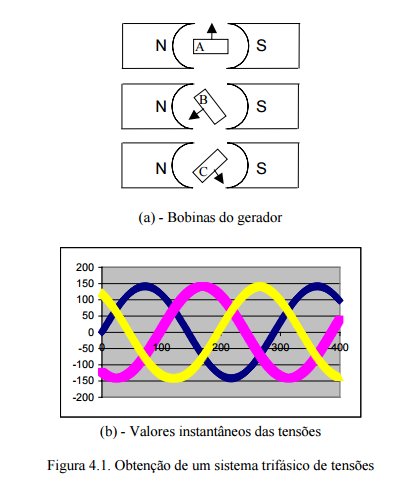
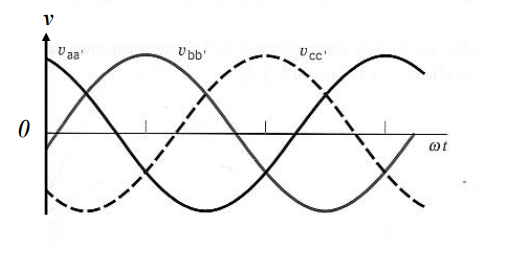
Isto é feito dispondo-se sobre o mesmo eixo, três bobinas deslocadas entre si de 2π/3 rad e girando o conjunto com velocidade angular constante no sentido horário, no interior de um campo magnético uniforme. Nos terminais das bobinas aparecerá um sistema de tensões de mesmo valor máximo e defasadas entre si de 2π/3 rad , conforme a Figura:

Define-se, para um sistema polifásico simétrico, “seqüência de fase” como sendo a ordem pela qual as tensões das fases passam pelo seu valor máximo.

Por exemplo, no sistema trifásico da Figura. 4.1, a seqüência de fase é A-B-C, uma vez que as tensões passam consecutivamente pelo valor máximo na ordem A-B-C.

Evidentemente, uma alteração cíclica não altera a seqüência de fase, isto é, a seqüência A-B-C é a mesma que B-C-A e que C-A-B.

À seqüência A-B-C é dado o nome “seqüência direta” ou “seqüência positiva”, e à seqüência A-C-B, que coincide com C-B-A e B-A-C, dá-se o nome de “seqüência inversa” ou “seqüência negativa”.

Exemplo

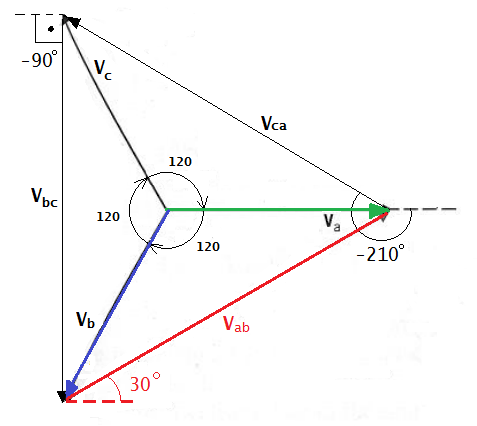
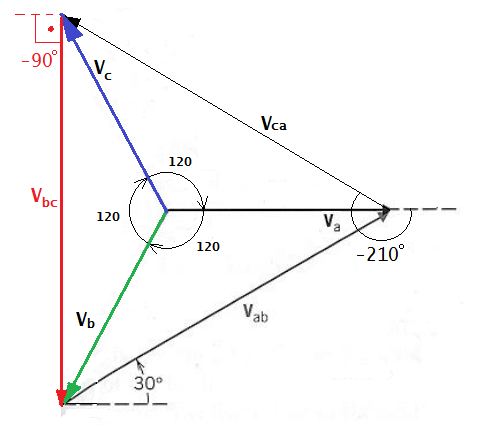
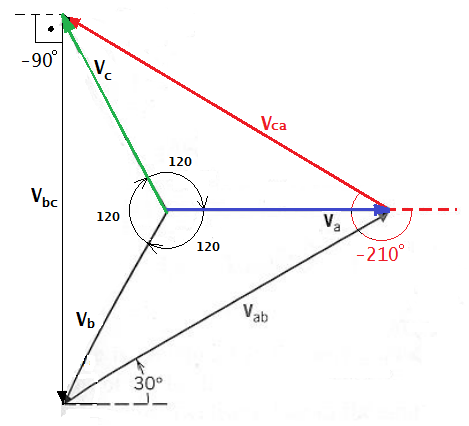
Um sistema trifásico simétrico tem seqüência de fase negativa, B-A-C, e VC = 220 ∠ 40° V . Determinar as tensões VA e VB .

---

Solução:

Sendo a seqüência de fase B-A-C, a primeira tensão a passar pelo valor máximo será VB , a qual será seguida, na ordem, por VA e VC . Portanto, deverá ser:

VB = Vm. cos( ωt +  θ)

VA = Vm. cos( ωt +  θ - 2π/3)

VC = Vm. cos( ωt +  θ - 4π/3)

em que θ representa o ângulo inicial ou a rotação de fase em relação à origem.

No instante t=0, tem-se:

VB = Vm. cos(θ)

VA = Vm. cos(θ - 2π/3)

VC = Vm. cos(θ - 4π/3)

Sendo V = Vm/ √2 , fasorialmente tem-se:

VB = V ∠ θ

VA = V ∠ (θ - 2π/3)

VC = V. ∠(θ - 4π/3)

Por outro lado, sendo dado VC = 220 ∠ 40° V , resulta

V = 220 V 

θ + 120 = 40° → θ = − 80° 

e portanto

VB = 220 ∠ − 80°

VA = 220 ∠ − 200°

VC = 220. ∠ − 40°

Tensão composta

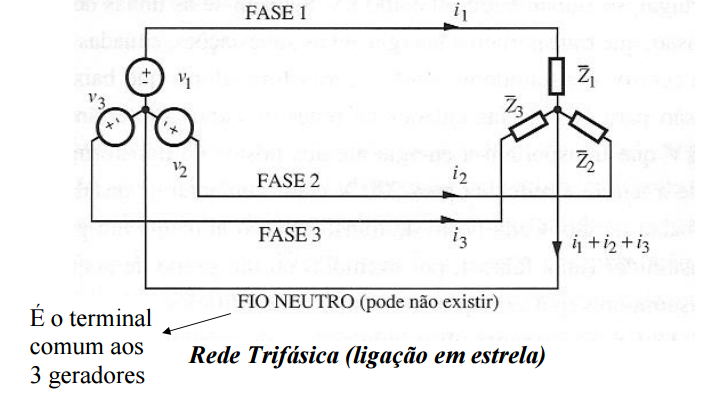
Redes Trifásicas

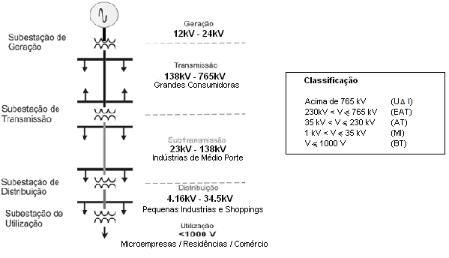
O sistema de produção, transporte e distribuição de energia elétrica tem a seguinte constituição:

Nas centrais há geradores de corrente alternada (acionadas por turbinas hidráulicas ou máquinas térmicas). Nas grandes usinas geradoras o nível de tensão na saída dos geradores está normalmente na faixa de 6 a 25 kV.

Para poder ser transmitida, a tensão produzida é, então, elevada. As tensões usuais de transmissão adotadas no Brasil, em corrente alternada, podem variar de 138 kV até 765 kV, incluindo neste intervalo as tensões de 230 kV, 345 kV, 440 kV e 500 kV.

O transporte de energia elétrica é feita pelas linhas de alta tensão até às subestações, situadas junto dos centros consumidores.

Os sistemas ditos de subtransmissão contam com níveis mais baixos de tensão, tais como 34,5 kV, 69 kV ou 88 kV e 138 kV e alimentam subestações de distribuição, cujos alimentadores primários de saída operam usualmente em níveis de 13,8 kV.

Junto aos pequenos consumidores existe uma outra redução do nível de tensão para valores entre 110 V e 440 V, na qual operam os alimentadores secundários. Nas cidades, há redes de cabos aéreos e subterrâneos que transportam a energia até aos pontos de transformação onde a tensão é reduzida a 110V ou 220V, para alimentar instalações de baixas tensão.

Cada posto de transformação alimenta um grande consumidor, fábrica, ou um grupo de pequenos consumidores, conjunto de edifícios residenciais.

O transporte da energia elétrica é feito em alta tensão para reduzir as perdas: P = Vef. Ief. cosϕ .

Para a mesma potência, se a tensão for maior, a corrente é menor, logo as perdas nos condutores, Ief². R, são menores.

O sistemas de produção, transporte e distribuição de energia elétrica constitui uma rede trifásica, com várias vantagens:

• Usam-se apenas 3 ou 4 condutores (fase 1,2,3, neutro) em vez de 6 (no caso de 3 redes monofásicas separadas)
• Nos geradores e motores o binário é constante (ausência de vibração)
• Motores e geradores são mais simples.

Na conexão estrela podemos calcular o valor eficaz das tensões de linha a partir dos valores eficazes das tensões de fase:

V linha =√3 Vfase 

E as correntes de fase são idênticas às correntes de linha, pois a corrente que circula por uma das cargas é a mesma que circula por uma das fases.

Na conexão triângulo, ou delta, a tensão de fase é igual a tensão de linha pois a tensão aplicada sobre cada uma das cargas é a diferença entre as tensões aplicadas às cargas vizinhas. E os valores eficazes das correntes de linha podem ser calculadas com os valores eficazes das 'correntes de fase':

I linha=√3 Ifase

Pressupondo um sistema balanceado, que nem sempre ocorre na prática.

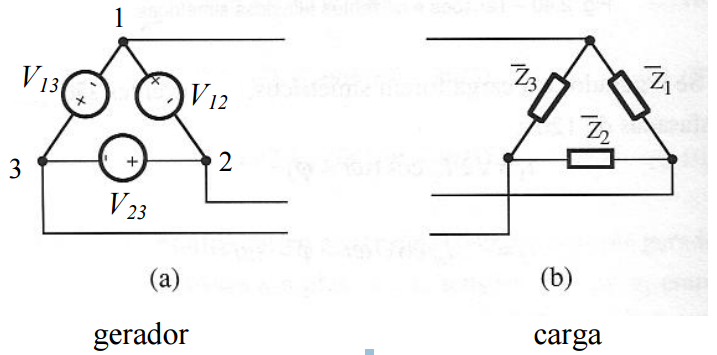
Um gerador trifásico simétrico é equivalente a um conjunto de três geradores iguais cujas tensões estão desfasadas de (120º) 2π/3:

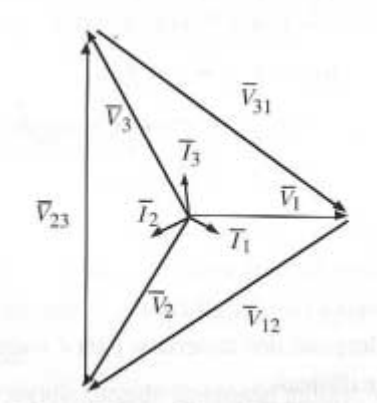
As tensões compostas são as tensões entre as fases v12, v23, v13, como se indica nos seguinte diagrama vetorial.

O valor eficaz das tensões compostas V∆ef é

V∆ef = 2 Vef .cos(π / 6) = √3 Vef. 

Por exemplo: na rede de distribuição em baixa tensão, a tensão simples é Vef = 220 V e a tensão composta, V∆ef = 380V.

Uma carga trifásica simétrica é constituída por 3 impedâncias iguais:

Se o gerador e a carga forem simétricos, as correntes serão iguais e desfasadas de 120º:

Numa rede trifásica simétrica tem-se, assim,

i1+ i2 +i3 = 0 

A potência fornecida pelo gerador à carga é:

p(t) = v1.i1 + v2.i2 + v3.i3

Se a rede trifásica for simétrica, potência instantânea é constante:

p(t) = 3.Vlinha,ef . I ef .cosϕ

EXEMPLO:

Um sistema trifásico a 4 condutores, (tensão composta V∆ef = 208V) alimenta uma carga em estrela equilibrada, constituída por impedâncias 20∠−30º . Calcular as correntes da linha e a potência fornecida pelos geradores.

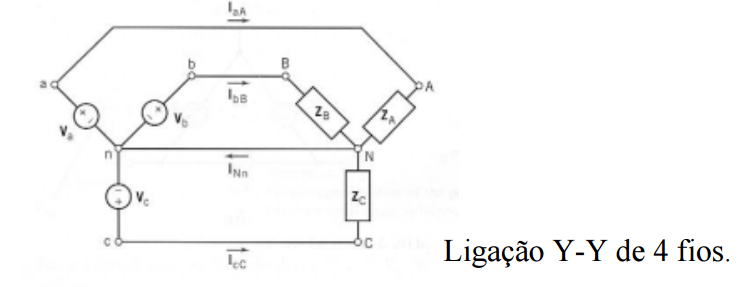
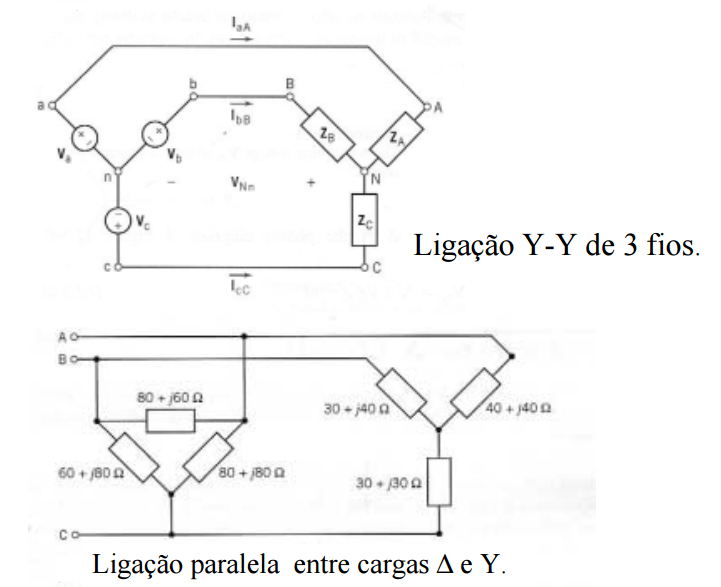
Sistema Y Equilibrado

Ligação em triângulo ou delta

Tanto o gerador quanto a carga podem ser ligados em triângulo, como seguir indica a figura,

As cargas são aplicadas às tensões compostas.

A corrente por fase e na linha não são coincidentes e a tensão nas cargas corresponde à tensão composta.

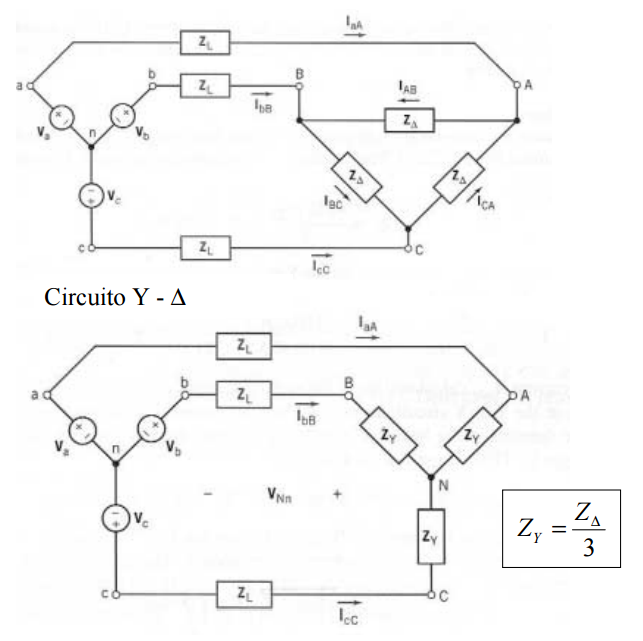
O gerador e a carga não têm de ser necessariamente em estrela ou ambos em triângulo: pode um ser em estrela e o outro em triângulo (Y-∆) .

Em qualquer caso , a potência transmitida, se a rede for simétrica, pode sempre calcular-se através de

Sistema ∆ Equilibrado

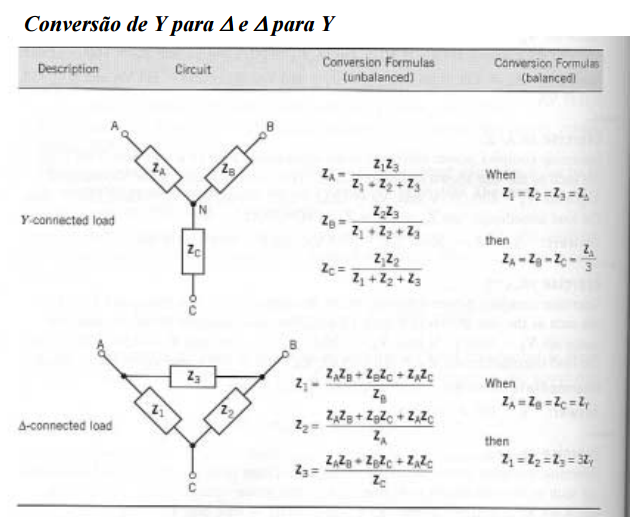
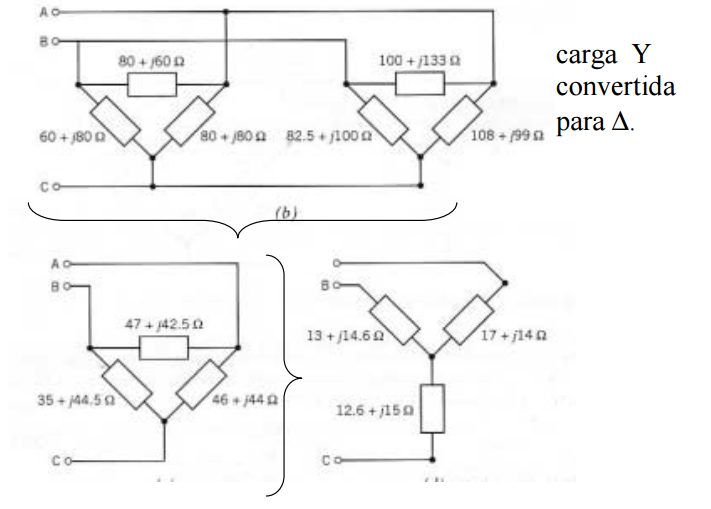
= ϕ - é o argumento das impedâncias na carga V∆ef - é a tensão entre fios da linha (tensão composta) Ief - é a corrente na linha 3 ∆ = Z ZY Circuito Y - ∆ O Circuito equivalente Y - Y 11 Circuito ∆-∆ equilibrado p=phase, L=line Conversão de Y para ∆ e ∆ para Y