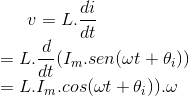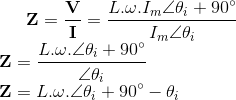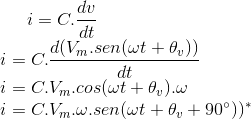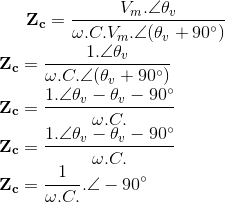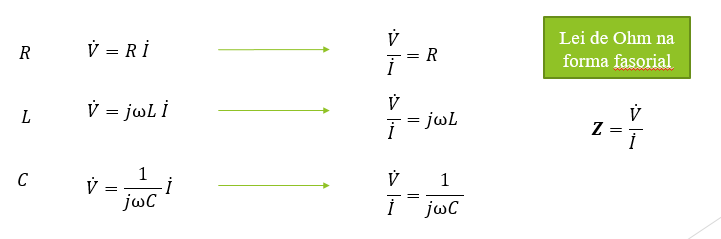AULA 2 - Circuitos Elétricos 2 - Graduação
Reatâncias e Impedâncias
Em corrente alternada, o valor da resistência dos componentes passivos (resistor, capacitor e indutor) é chamado de impedância, que é formada por reatâncias.
Define-se impedância como a relação entre o fasor de tensão V e o fasor de corrente I:
A impedância é expressa em Ohms [Ω].
Assim, a impedância em um circuito CA é análoga à resistência, em um circuito CC.
Na forma retangular, a impedância é expressa como:
onde R(ω) é a componente real, ou resistiva e X(ω) é a componente imaginária, ou reativa.
Em geral, refere-se a R como resistência e à X, como reatância.
Vamos agora analisar estas reatâncias, devidas aos elementos de circuitos:
Representação fasorial de resistores
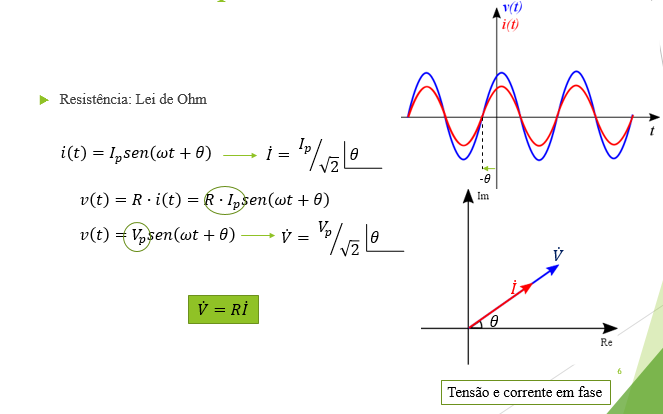
Para o resistor, a impedância é igual ao valor da resistência em CC, e ângulo de fase igual a zero.
Assim, os sinais de corrente e tensão permanecem EM FASE, no circuito puramente resistivo.
Características
A grandeza
é, então, denominada impedância do elemento resistivo.
É medida em Ω e representa a resistência à passagem de corrente no circuito.
É importante, porém, salientar que ![]() não é um fasor!, porque não varia no tempo, à velocidade angular ω.
não é um fasor!, porque não varia no tempo, à velocidade angular ω.
Enfim, a impedância do elemento resistivo NÃO DEPENDE da frequência ω do circuito!!!
Quanto maior a resistência em um circuito, menor será a corrente elétrica, exatamente porque a resistência se refere à capacidade de oposição à corrente.
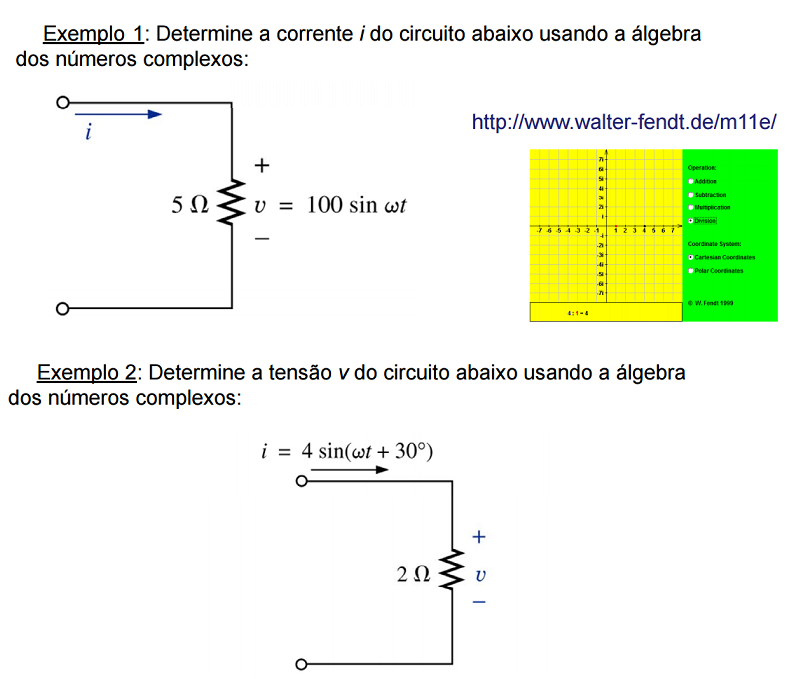
Exercícios:
Representação fasorial de indutores
Relação entre tensão e corrente no indutor
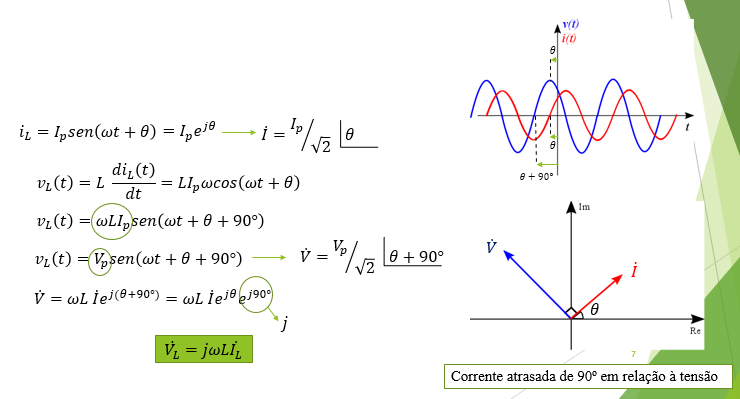
Podemos deduzir a relação entre a corrente fasorial e a tensão fasorial nos terminais de um indutor admitindo uma corrente senoidal:
i = Im.sen(ωt + θi)
e usando a relação:
v = L.di/dt
para calcular a tensão correspondente:
uma vez que a sen'(u) = cos(u).u' (vide [1]).
Também sabe-se (vide [2]) que cos α = sen(α + 90º), portanto:
Comparando-se os dois termos, para corrente e tensão:
ou:
e, portanto:
Note que, no indutor, a corrente está ATRASADA de 90°, ou π/2, em relação à tensão!!!
Em outras palavras:
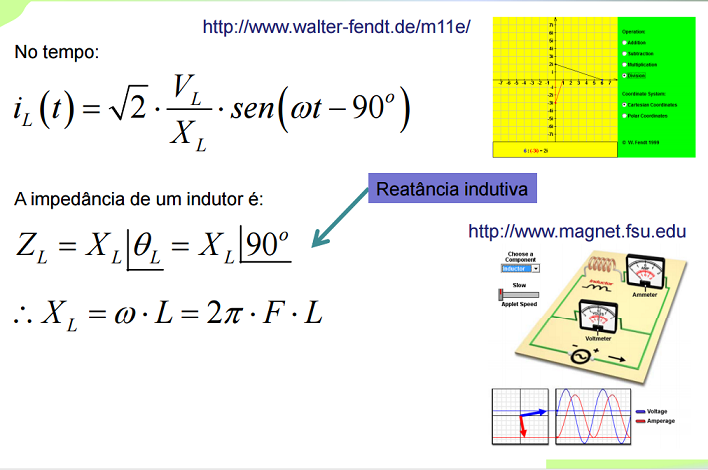
Portanto, a impedância do indutor introduz um ângulo de fase de 90 graus no circuito.
Assim, o sinal de corrente ficará ATRASADO, em relação à tensão, no circuito indutivo.
Características
A reatância indutiva é uma oposição à corrente e é DIRETAMENTE PROPORCIONAL à taxa de variação da corrente que atravessa o indutor, isto é, diretamente proporcional à frequência ω.
Quanto maior a frequência de oscilação da alimentação do circuito, MAIOR a reatância indutiva!
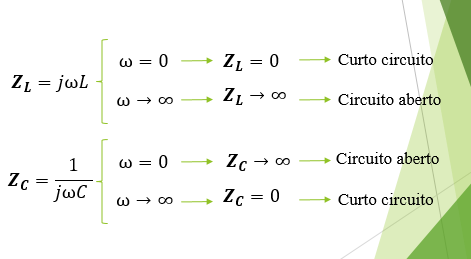
Se ω→∞ ⇒ XL →∞
Além disto, por ser uma impedância imaginária, ao contrário da resistência, a reatância indutiva NÃO DISSIPA ENERGIA ELÉTRICA (ignorando-se os efeitos da resistência interna do indutor)!
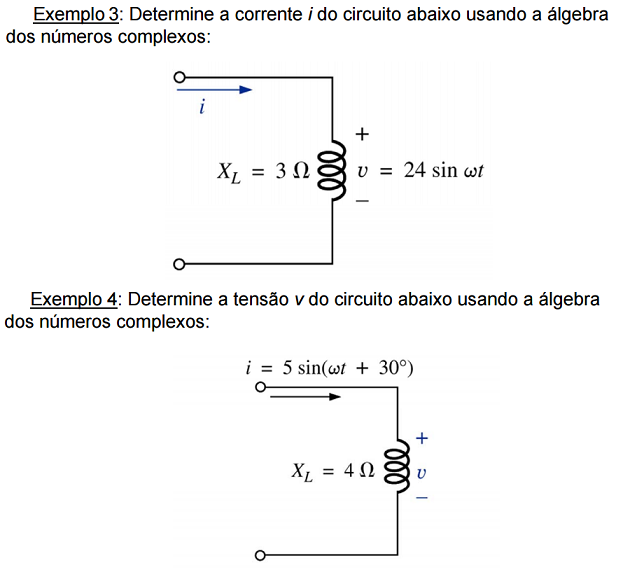
Exercícios:
Representação fasorial de capacitores
Relação entre tensão e corrente
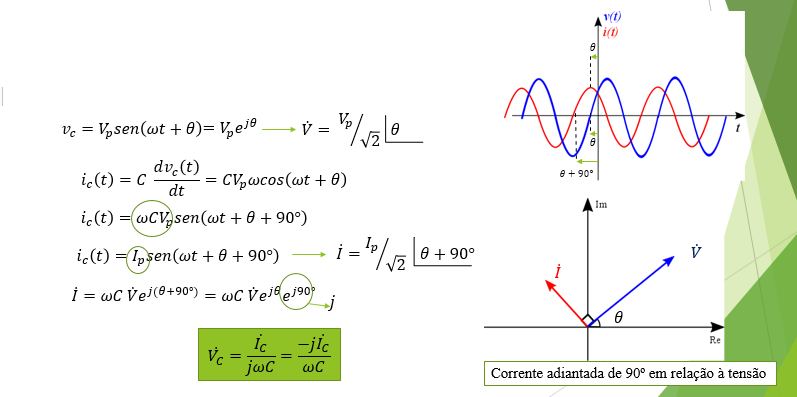
Podemos deduzir a relação entre a corrente fasorial e a tensão fasorial nos terminais de um indutor admitindo uma tensão senoidal Vm.sen(ωt + θv) e usando a relação i = C.dv/dt para calcular a tensão correspondente:
uma vez que a * seno'(u) = cos(u).u' (vide [3]) e que cos α = sen(α + 90º).
No formato fasorial:
Ou seja,
No capacitor, a corrente está ADIANTADA de 90°, ou π/2, em relação à tensão!
Mas:
portanto:
Em outras palavras:
Ou seja, a impedância devida ao capacitor introduz um ângulo de fase de -90 graus no circuito.
Assim, o sinal de corrente ficará ADIANTADO, em relação à tensão, no circuito capacitivo.
Características
A reatância capacitiva é uma oposição à corrente e é INVERSAMENTE PROPORCIONAL à taxa de variação da corrente que atravessa o capacitor, isto é, inversamente proporcional à frequência ω.
Quanto maior a frequência de oscilação da alimentação do circuito, MENOR a reatância indutiva!
Se ω→∞ ⇒ XC →0
Este efeito é bastante explorado no que se chamam capacitores de acoplamento e desacoplamento.
Além disto, por ser uma impedância imaginária, ao contrário da resistência, a reatância capacitiva TAMBÉM NÃO DISSIPA ENERGIA ELÉTRICA (ignorando-se os efeitos da resistência de fuga)!
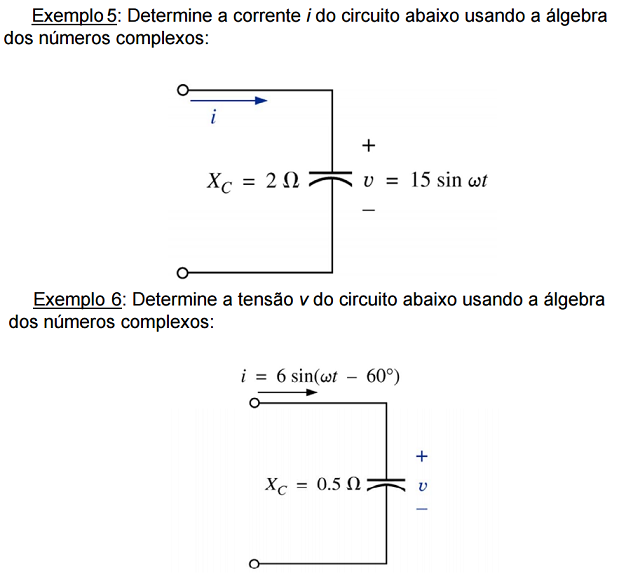
Exercícios:
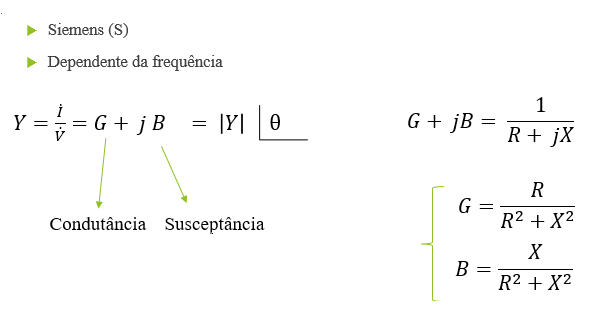
Impedância e Admitância
TABELA RESUMO
A unidade de todas estas grandezas é o [Ω].
| Elemento de circuito | Impedância | Reatância |
|---|---|---|
| Resistor | R | - |
| Indutor | j |
|
| Capacitor | j |
Impedância
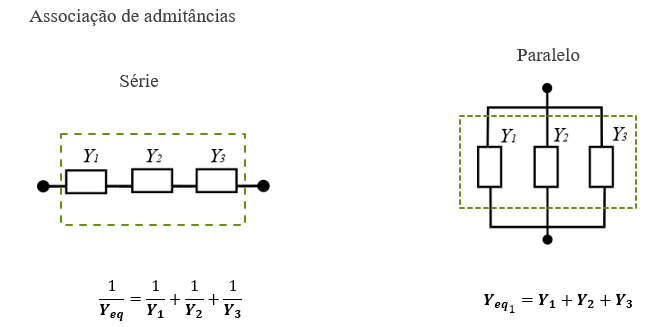
Admitância
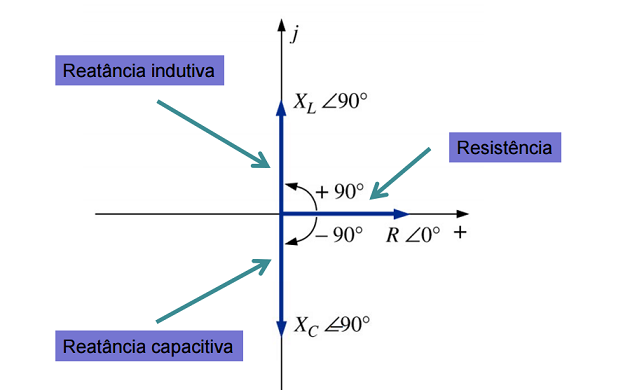
Diagramas de fasores
Um diagrama fasorial é uma representação de fasores no plano complexo.
Graficamente, as impedâncias e fasores podem ser representados, então, da seguinte forma:
IMPORTANTE!
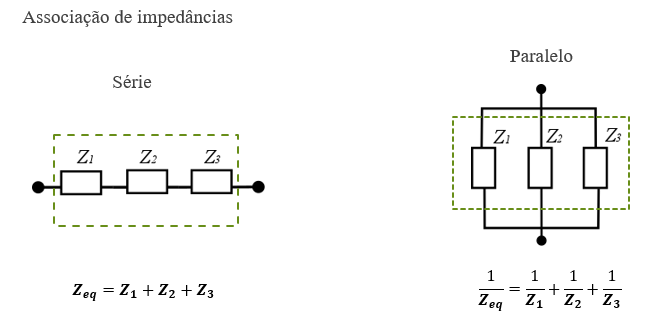
A impedância total de um circuito, então, será sempre uma soma vetorial dos valores das impedâncias individuais dos elementos do circuito.
Exercícios:
- Problemas para avaliação, pg 239, Nilsson&Riedel.
- Seções 14.3 e 14.4, pgs. 438 e 439, Boylestad.
Frequência Complexa
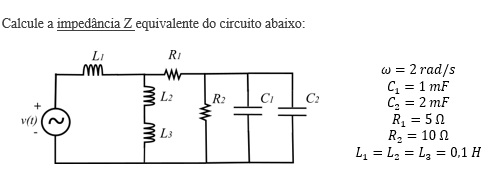
Exercício
Bibliografia
[1] SADIKU, M. N. O.; MUSA, S. M.; ALEXANDER, W. K. Análise de Circuitos Elétricos com Aplicações. Porto Alegre: Mc Graw Hill Education, 2014. v. 3.
[2] BOYLESTAD, R. L. Introdução à Análise de Circuitos. 12a ed. São Paulo: Pearson, 2011.
[3] PETRY, C. Circuitos 2. Disponível em: Aula 4 - Impedância e Reatância, 2023.
| << Revisão, Geração CA e Fasores | Reatâncias e Impedâncias | Lei de Ohm, Divisor de corrente/tensão e Leis de Kirchoff em CA, RP >> |
|---|