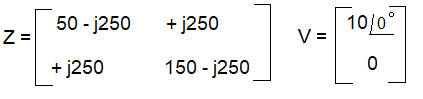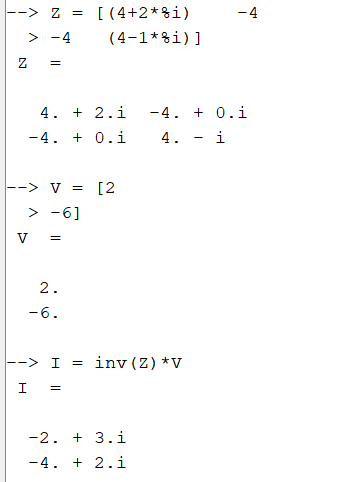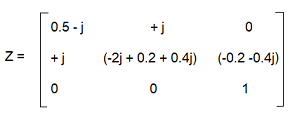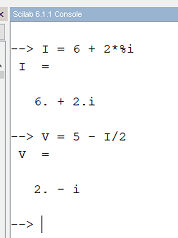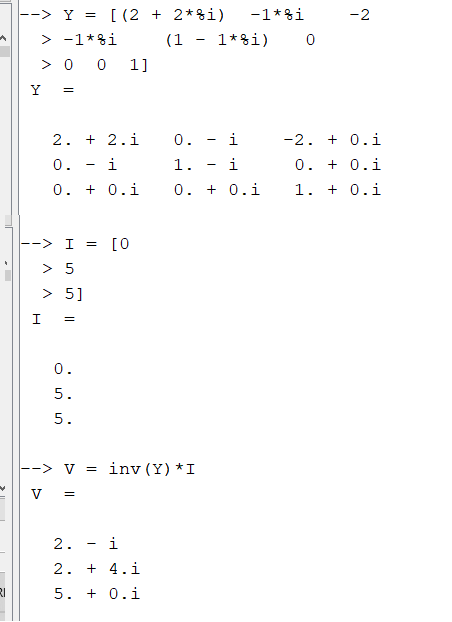AULA 3 - Circuitos Elétricos 2 - Graduação

<< Página do curso

Técnicas e Teoremas em CA Regime Permanente

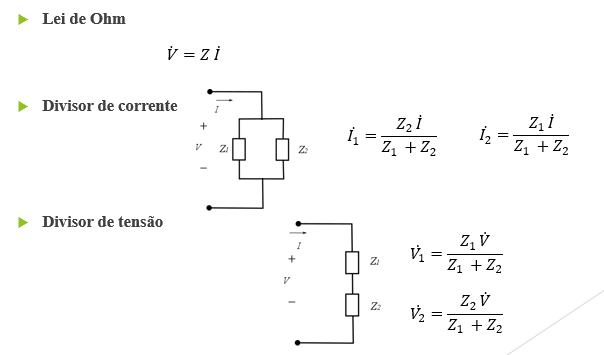
Lei de Ohm, Divisor de corrente/tensão e Leis de Kirchoff (tensão e corrente) em CA, regime permanente

Lei de Kirchoff para as tensões

A soma das tensões em uma malha fechada é igual a zero.

Este método é o mais indicado quando N_malhas < N_nós do circuito!!!

Método de Análise simples

1. Identificar todas as M malhas internas do circuito
2. Arbitrar uma corrente I_m percorrendo cada malha
3. Percorrer a malha m, computando a soma das tensões:
   1. Fontes de tensão: entra com seu valor direto, observando a polaridade da fonte, com relação ao sentido da corrente;
   2. Tensão na Impedância Z_m: tensão = I_m.Z_m;
   3. Fontes de corrente: adiciona uma variável de tensão a determinar, mas elimina um valor de corrente I_m no ramo;
   4. Fontes dependentes: adiciona uma variável a determinar (+ uma equação).
4. Resolve o sistema de equações (matricial ou por substituição)

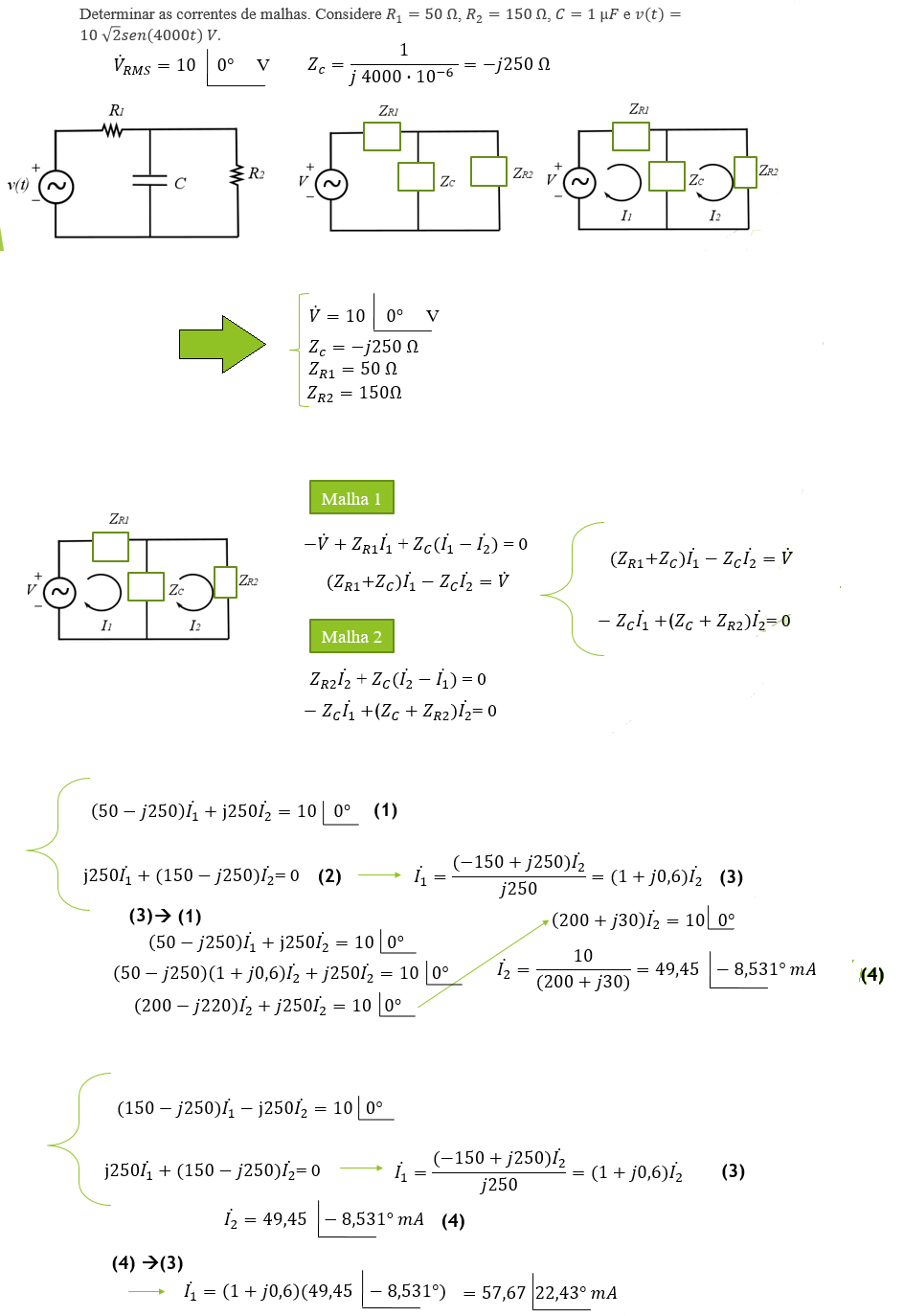
Exemplo 1:

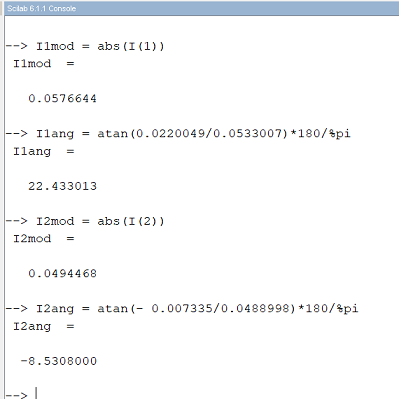
Em valores eficazes. Ou I₁ = 81,31 ∠ 22,43° mA, de pico e I₂ = 69,73 ∠ -8,531° mA, de pico.

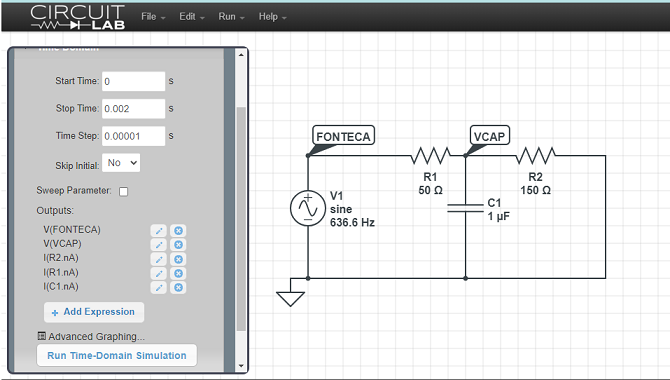
Simulação:

Para verificar, vamos simular este circuito no CircuitLab:

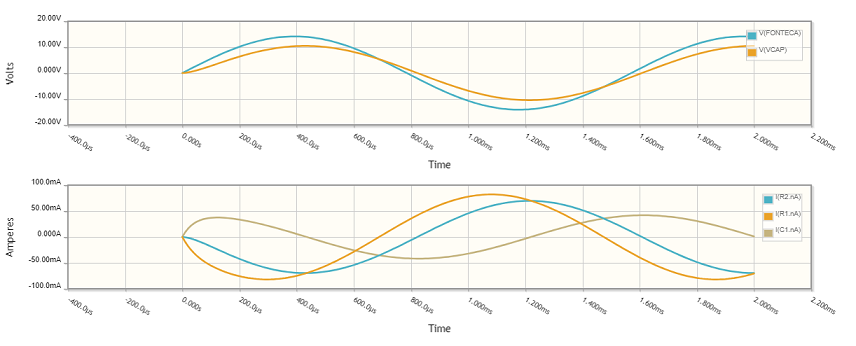
Note que utilizamos uma janela de Δt = 0,002 s porque, se ω = 4.000 rad/s = 2.π.f → f = 636,62 Hz e, portanto, T=0,0015708 s.

As correntes I₁ e I₂ correspondem às curvas I_R1 e I_R2, respectivamente, e V_x corresponde à curva V_CAP.

Método de Análise sistemática

A análise sistemática, que pode ser mais facilmente automatizada, consiste em organizar o sistema de equações do circuito na forma:

I = V.Z-1 

onde:

• V é a matriz coluna (N x 1), contendo os valores das fontes de tensão das malhas;
• Z é a matriz quadrada (N x N), contendo as impedâncias do circuito, e
• I é a matriz coluna (N x 1), contendo as correntes de malha, que se quer determinar;

onde N é o número de malhas do circuito.

A partir disto, a solução do circuito consistirá em inverter computacionalmente a matriz de impedâncias Z, e multiplicá-la pela matriz de fontes de tensão V.

Assim, para cada malha i do circuito, contendo apenas fontes de tensão, a matriz Z será construída da seguinte forma:

1. Em cada posição da diagonal principal, os elementos z_{i i} serão dados pelo somatório de todas as impedâncias daquela malha i;
2. Os elementos z_{i j} serão dados pelo somatório das impedâncias mútuas entre as malhas i e j com o sinal trocado;
3. Como a matriz é SIMÉTRICA, os elementos z_{i j} = z_{j i};
4. Se duas malhas não possuem impedâncias em comum, o elemento da matriz correspondente será nulo.

Cada linha i da matriz V é composta pelo somatório das fontes de tensão da malha i, observando-se as seguintes polaridades:

• Fonte de tensão com corrente arbitrada entrando no pólo NEGATIVO da fonte: valor POSITIVO;
• Fonte de tensão com corrente arbitrada entrando no pólo POSITIVO da fonte: valor NEGATIVO.

Análise Sistemática do Exemplo 1

Vamos fazer o levantamento da matriz de impedâncias Z_2x2 e da matriz de fontes de tensão V_2x1.

Quais sejam:

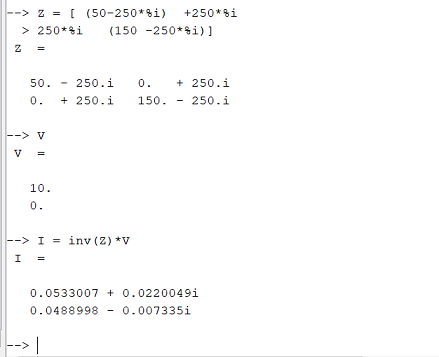
E aí será possível resolver o sistema de equações no Scilab, da forma:

Em coordenadas polares:

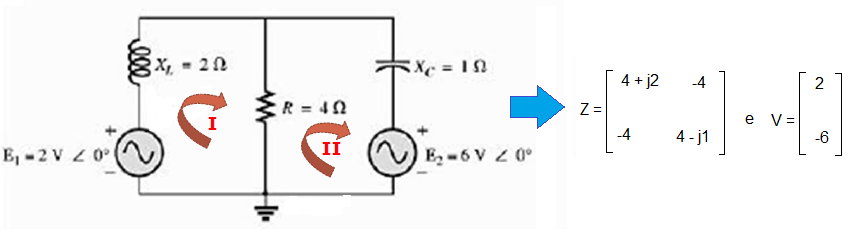
Exemplo 2:

Seja o circuito abaixo e suas matrizes de impedância e fontes de tensão:

Análise Sistemática do Exemplo 2

A análise deste circuito no Scilab será:

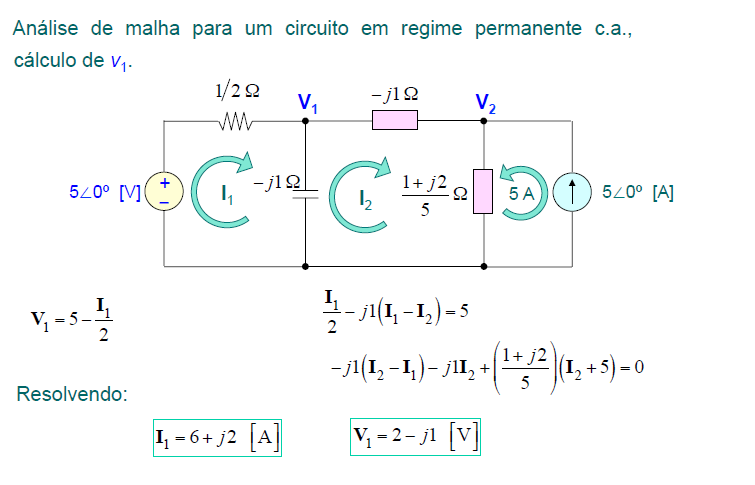
Exemplo 3:

Análise Sistemática do Exemplo 3

A análise sistemática deste circuito precisa considerar a fonte de corrente de 5A.

Basta incluir apenas as 2 equações das malhas 1 e 2, na matriz impedância, mas também uma terceira equação, que simplesmente relaciona a corrente da 3a. malha, com a fonte.

Qual seja:

                1. I3 = -5A

Assim, a matriz de impedâncias ficará:

Ou seja, a terceira linha, não será uma equação de tensão da forma Z _{x y} .I_x, como as demais equações. Esta equação, como se refere a uma fonte de corrente, incluirá apenas o valor da CORRENTE de malha, I₃, pois não é possível determinar-se a tensão nesta fonte.

Assim, torna-se possível resolver o sistema de equações no Scilab, da forma:

Note que a última equação, novamente, estabelece que I₃ = -5A, como esperado.

E a tensão V1 será:

Lei de Kirchoff para as correntes

A soma das correntes em um nó é igual a zero.

Este método é o mais indicado quando N_nós < N_malhas do circuito!!!

Método de Análise simples

1. Identificar todos os N nós do circuito;
2. Arbitrar uma tensão V_n em cada nó;
3. Transformar todas as impedâncias do circuito em admitâncias: Y_k=1/Z_k;
4. Computar todas as correntes i_n, de todos os ramos que chegam ao nó, adicionando os elementos de circuito conectados ao nó desta forma:
   1. Fontes de tensão: adiciona uma variável/incógnita de corrente, porém já provê a tensão direta do nó: V_n = (+-)V_fonte, observada a polaridade;
   2. Admitância Y_n: corrente na admitância = (V_n - V_m).Y_n (ou como (V_n - V_m)/Z_n, se as impedâncias não foram transformadas em admitâncias); onde V_m é a tensão no nó adjacente do ramo, a qual entra no somatório com valor negativo, em relação à tensão do nó;
   3. Fontes de corrente: se a corrente da fonte chega no nó, ela entra com valor negativo no somatório, e positivo, caso contrário;
   4. Fontes dependentes: adiciona uma variável a determinar (+ uma equação).
5. Resolve o sistema de equações (matricial ou por substituição)

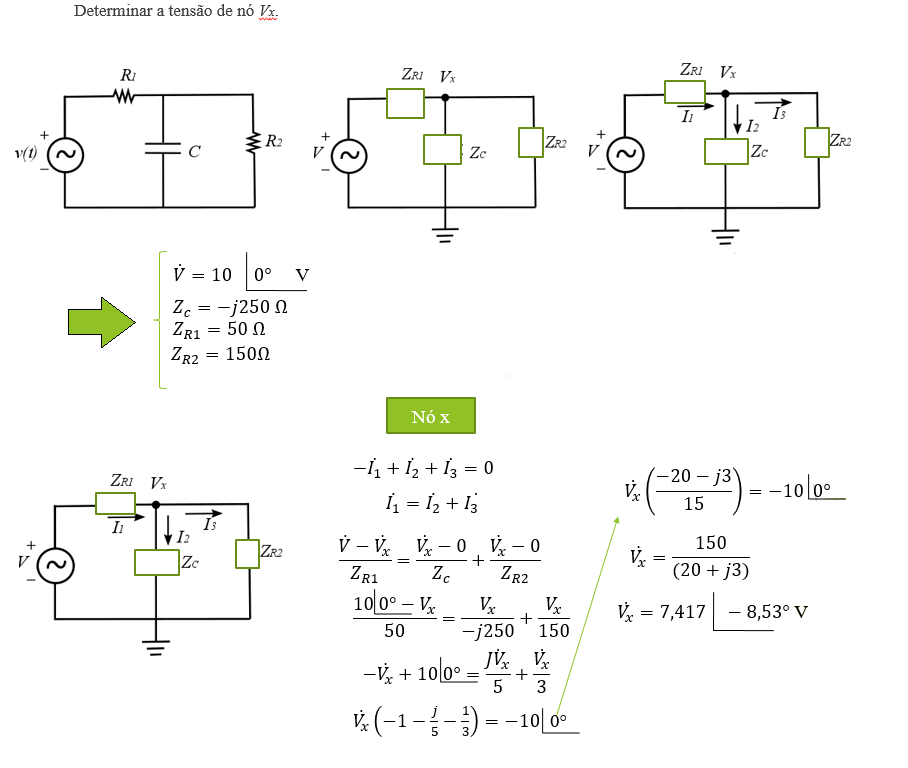
Exemplo 4:

Resolvendo pelo método simples:

Em valor eficaz. Ou V_x = 10,46 ∠ -8,53° V, de pico

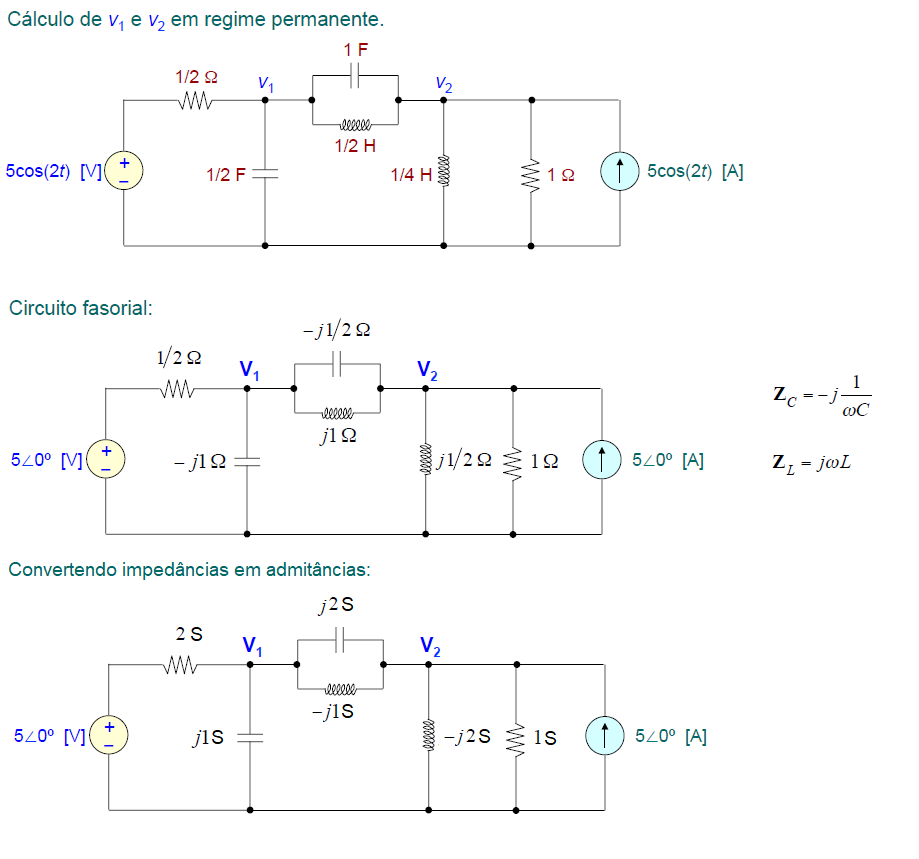
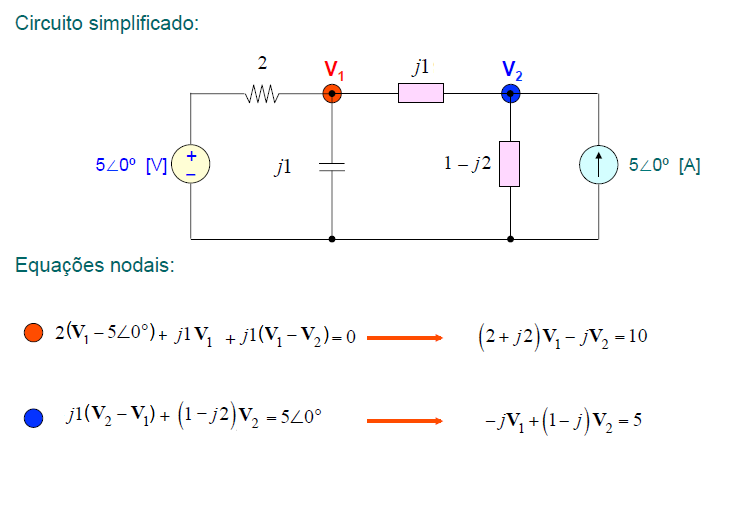
Exemplo 5:

O circuito abaixo tem 5 malhas, mas apenas 2 nós independentes (excetuando-se o nó de referência). Portanto, é mais fácil de analisar pelo Método dos Nós.

Resolvendo pelo método simples:

Método de Análise sistemática

A análise sistemática, que pode ser mais facilmente automatizada, consiste em organizar o sistema de equações do circuito na forma:

V = I.Y-1 

onde:

• I é a matriz coluna (N x 1), contendo os valores das fontes de correntes nos nós;
• Y é a matriz quadrada (N x N), contendo as admitâncias do circuito, e
• V é a matriz coluna (N x 1), contendo as tensões nos nós, que se quer determinar;

onde N é o número de nós independentes do circuito (excetuando-se a referência).

A partir disto, a solução do circuito consistirá em inverter computacionalmente a matriz de condutâncias Y, e multiplicá-la pela matriz de fontes de corrente I.

Assim, para cada nó i do circuito, contendo apenas fontes de corrente, a matriz Y será construída da seguinte forma:

1. Em cada posição da diagonal principal, os elementos y_{i i} serão dados pelo somatório de todas as admitâncias daquele nó i;
2. Os elementos z_{i j} serão dados pelo somatório das admitâncias mútuas entre os nós i e j com o sinal trocado;
3. Como a matriz é SIMÉTRICA, os elementos z_{i j} = z_{j i};
4. Se dois nós não possuem admitâncias em comum, o elemento da matriz correspondente será nulo.

Cada linha i da matriz V é composta pelo somatório das fontes de corrente ligadas ao nó i, observando-se as polaridades:

• Fonte de corrente com a corrente ENTRANDO no nó - valor positivo
• Fonte de corrente com a corrente SAINDO do nó - valor negativo

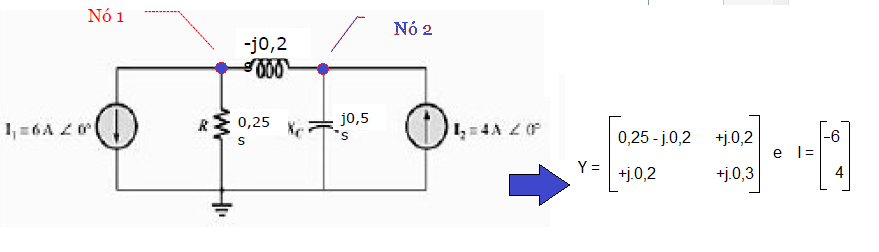
Exemplo 6

Seja o circuito com 2 nós abaixo, e suas matrizes de admitância Y e fontes de corrente I:

A análise sistemática no Scilab será:

Em coordenadas polares:

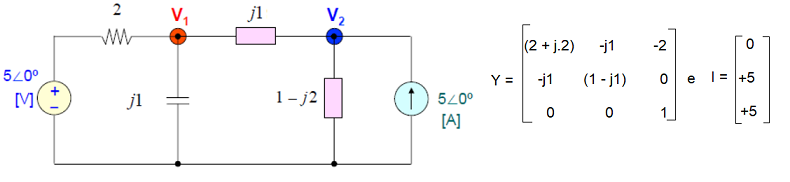
Exemplo 7

Seja o circuito abaixo e sua matriz de admitância. Como este circuito possui uma fonte de tensão, a matriz de fontes incluirá uma equação para tensão, e não apenas de correntes:

Como existe a fonte de tensão no circuito, devem ser incluídas apenas as equações dos nós que não têm fonte de tensão conectadas (no caso, apenas os nós 1 e 2) e a terceira equação, do que seria o nó 3 aonde está conectada a fonte de tensão, é tirada diretamente da relação:

1.V3 = 5V

e não das equações de corrente do tipo (Vx - Vy).Yxy.

A análise no Scilab será:

Confirmando os resultados obtidos pelo Método simples no Exemplo 5.

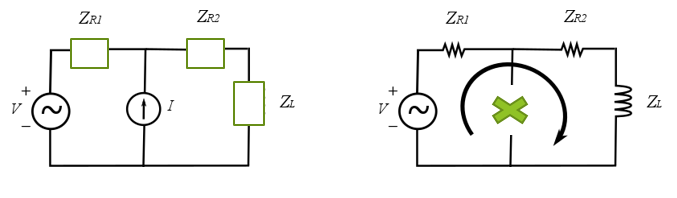
Supermalha

Adequada para circuitos que possuem malhas com fonte de corrente em comum.

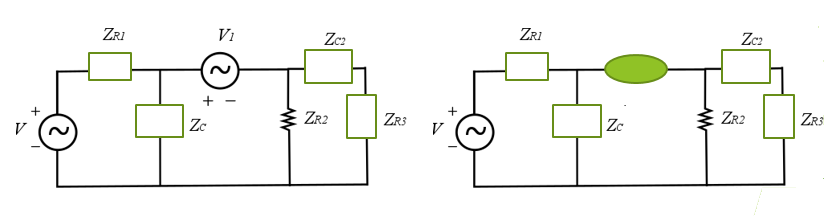
Supernó

Formado pela exclusão de uma fonte de tensão (dependente ou independente) conectada entre dois nós, com exceção do nó de referência, e qualquer elemento conectado em paralelo com ela.

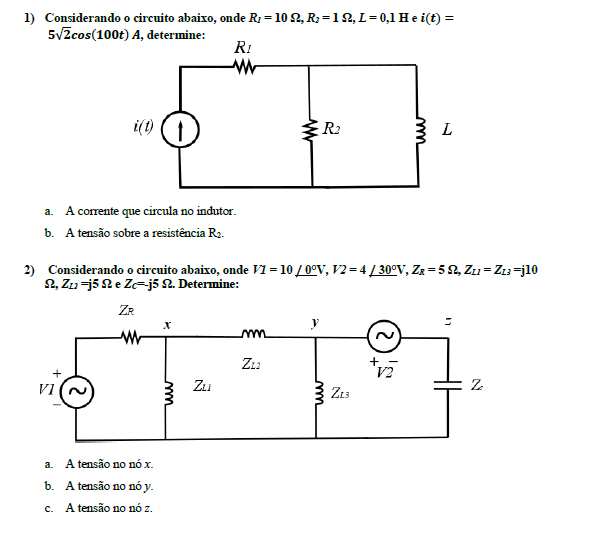
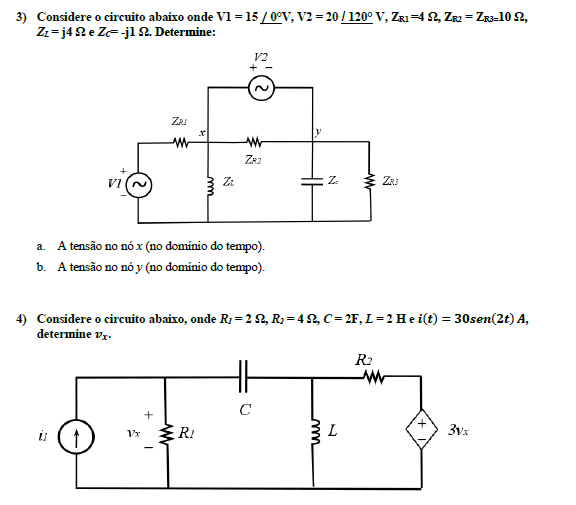
Exercícios

Resolução Exercícios 1 e 2

Resolução Exercícios 3 e 4

Bibliografia

[1] SADIKU, M. N. O.; MUSA, S. M.; ALEXANDER, W. K. Análise de Circuitos Elétricos com Aplicações. Porto Alegre: Mc Graw Hill Education, 2014. v. 3.

[2] BOYLESTAD, R. L. Introdução à Análise de Circuitos. 12a ed. São Paulo: Pearson, 2011.

[3] PETRY, C. Circuitos 2. Disponível em: Aula 4 - Impedância e Reatância, 2023.

[4] BALDINI Fo., Renato. EA-513 Circuitos Elétricos, Notas de Aula, Disponível em: Circuitos Elétricos, 2014.

---

<< Página do curso

<< Reatâncias e Impedâncias	Lei de Ohm, Divisor de corrente/tensão e Leis de Kirchoff em CA, RP	Equivalentes de Thevénin e Norton, RP >>