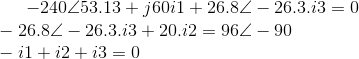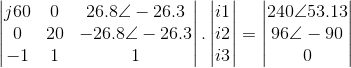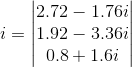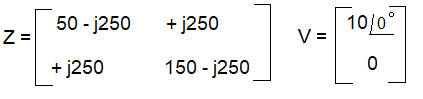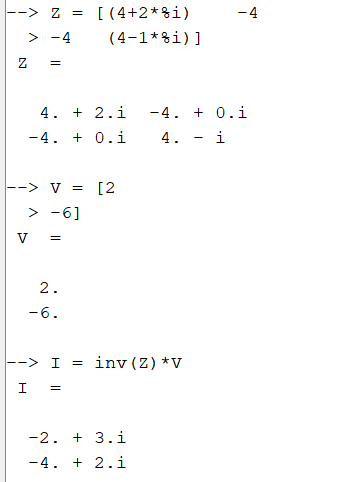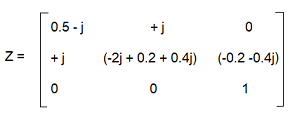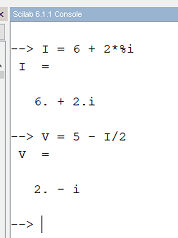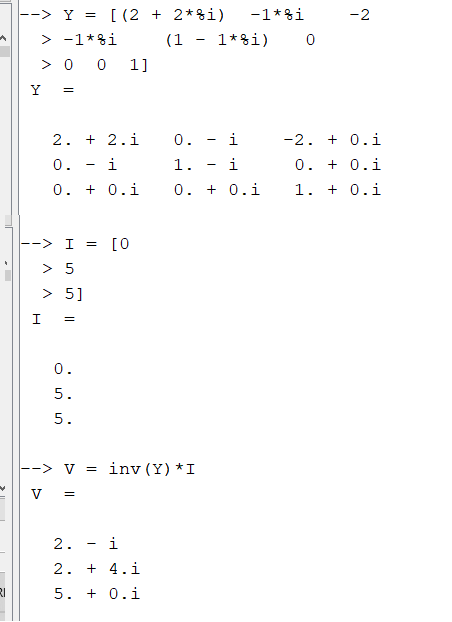AULA 3 - Circuitos Elétricos 2 - Graduação

<< Página do curso

Técnicas e Teoremas em CA Regime Permanente

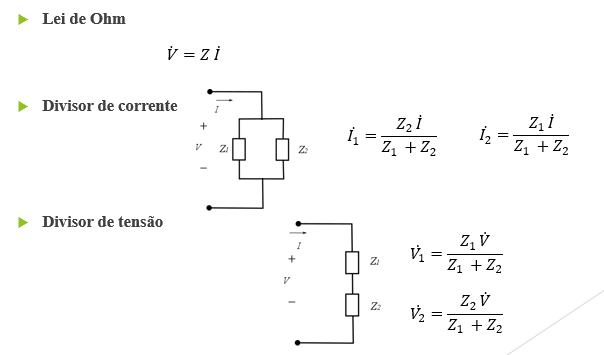
Lei de Ohm, Divisor de corrente/tensão e Leis de Kirchoff (tensão e corrente) em CA, regime permanente

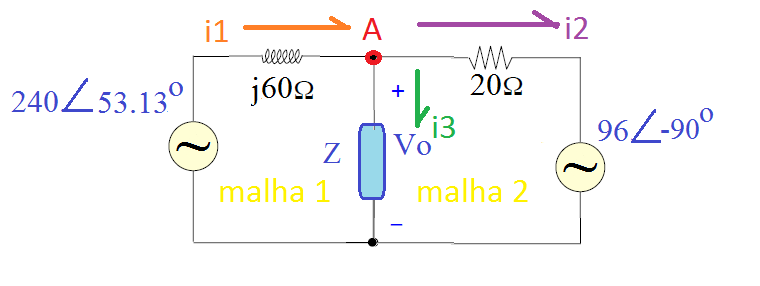
Análise de Kirchoff simples

A análise de Kirchoff consiste em:

1. identifica-se os N nós do circuito,
2. identifica-se as M malhas internas do circuito,
3. atribui-se uma corrente a cada ramo do mesmo,
4. calcular-se o somatório destas correntes em cada um dos nós e
5. calcular-se o somatório das tensões em cada malha.

Ou seja, cada circuito irá gerar (N + M) equações, menos (O + P), onde O é o número de correntes conhecidas e P, o número de tensões nos ramos conhecidas.

Exemplo:

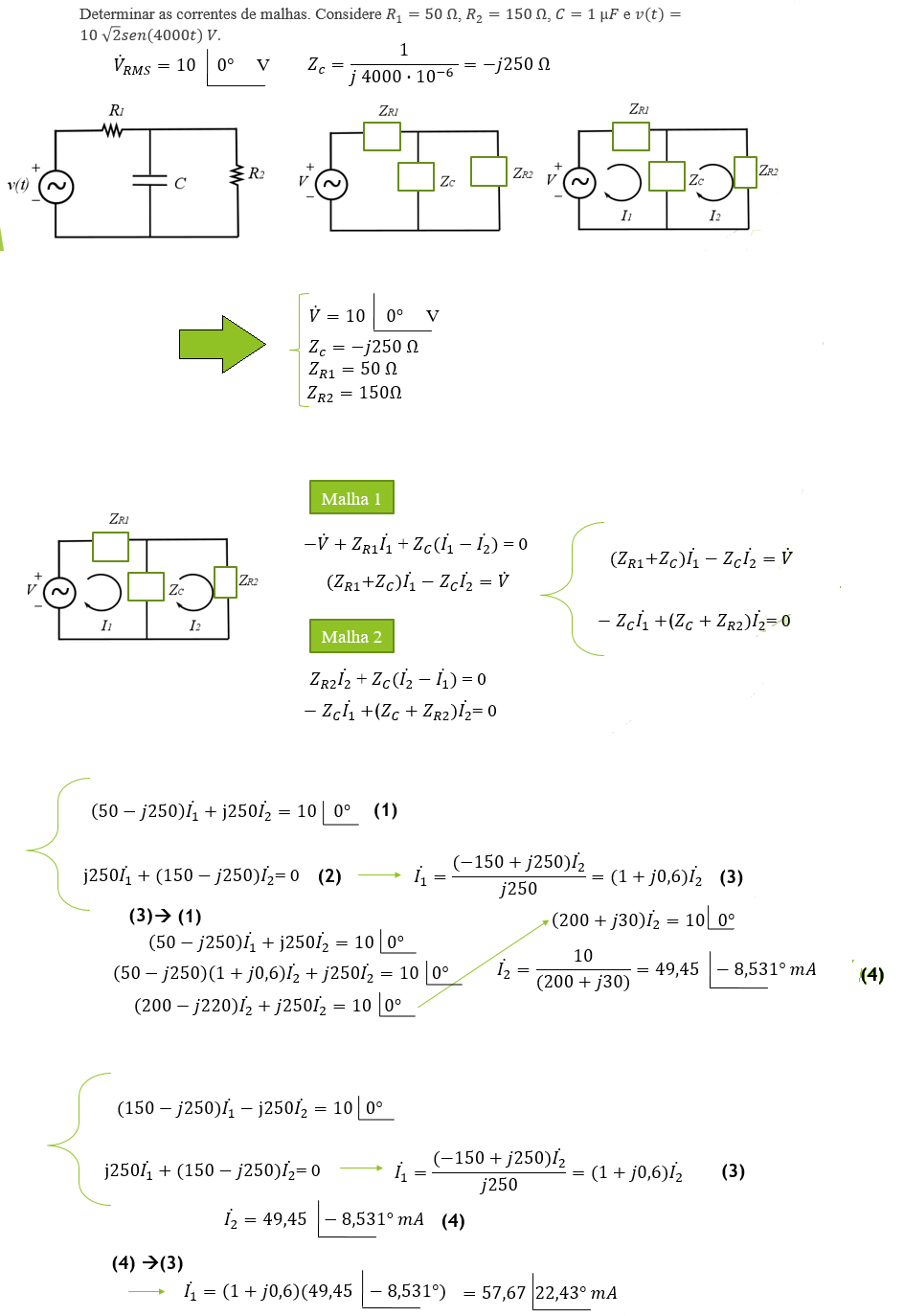
Analise o circuito abaixo agora utilizando análise de Kirchoff:

As 2 equações de malha mais a equação do nó A tornam-se:

Na forma matricial - Z.I = V:

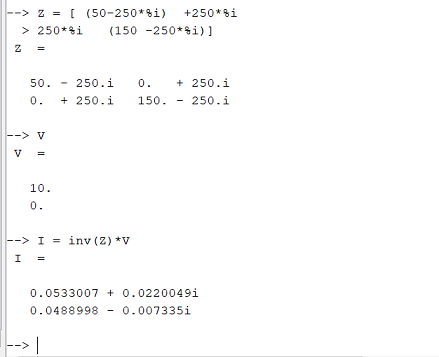
Resolvendo a equação acima da forma I = inversa(Z)*V obtém-se as correntes:

Mais informações: Análise de Kirchoff

Lei de Kirchoff para as tensões (KVL)

A soma das tensões em uma malha fechada é igual a zero.

Este método é o mais indicado quando N_malhas < N_nós do circuito!!!

Método de Análise simples

1. Identificar todas as M malhas internas do circuito
2. Arbitrar uma corrente I_m percorrendo cada malha
3. Percorrer a malha m, computando a soma das tensões:
   1. Fontes de tensão: entra com seu valor direto, observando a polaridade da fonte, com relação ao sentido da corrente;
   2. Tensão na Impedância Z_m: tensão = I_m.Z_m;
   3. Fontes de corrente: adiciona uma variável de tensão a determinar, mas elimina um valor de corrente I_m no ramo;
   4. Fontes dependentes: adiciona uma variável a determinar (+ uma equação).
4. Resolve o sistema de equações (matricial ou por substituição)

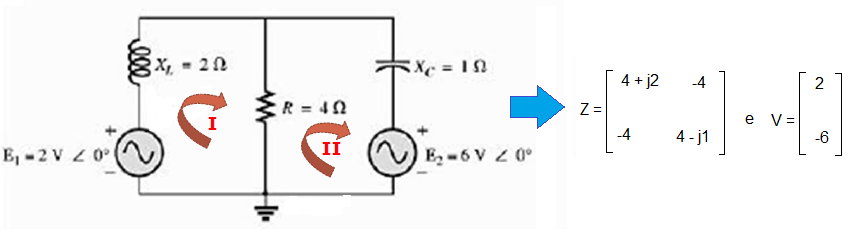
Exemplo 1:

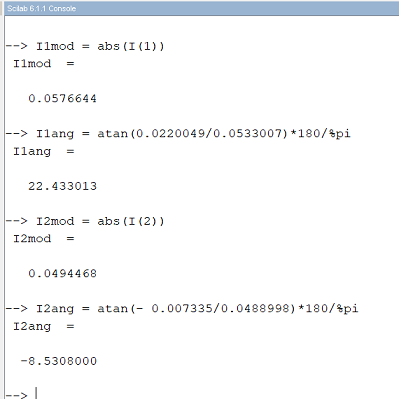
Em valores eficazes. Ou I₁ = 81,31 ∠ 22,43° mA, de pico e I₂ = 69,73 ∠ -8,531° mA, de pico.

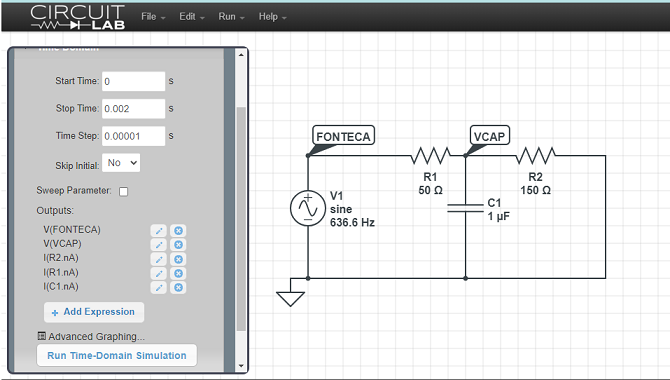
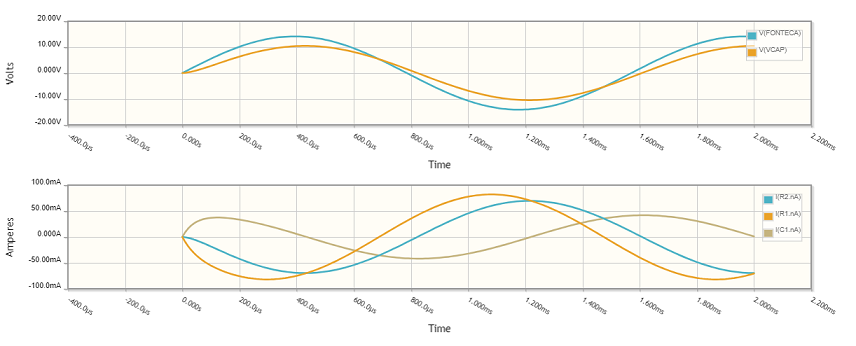
Simulação:

Para verificar, vamos simular este circuito no CircuitLab:

Note que utilizamos uma janela de Δt = 0,002 s porque, se ω = 4.000 rad/s = 2.π.f → f = 636,62 Hz e, portanto, T=0,0015708 s.

As correntes I₁ e I₂ correspondem às curvas I_R1 e I_R2, respectivamente, e V_x corresponde à curva V_CAP.

Método de Análise sistemática

A análise sistemática, que pode ser mais facilmente automatizada, consiste em organizar o sistema de equações do circuito na forma:

I = V.Z-1 

onde:

• V é a matriz coluna (N x 1), contendo os valores das fontes de tensão das malhas;
• Z é a matriz quadrada (N x N), contendo as impedâncias do circuito, e
• I é a matriz coluna (N x 1), contendo as correntes de malha, que se quer determinar;

onde N é o número de malhas do circuito.

A partir disto, a solução do circuito consistirá em inverter computacionalmente a matriz de impedâncias Z, e multiplicá-la pela matriz de fontes de tensão V.

Assim, para cada malha i do circuito, contendo apenas fontes de tensão, a matriz Z será construída da seguinte forma:

1. Em cada posição da diagonal principal, os elementos z_{i i} serão dados pelo somatório de todas as impedâncias daquela malha i;
2. Os elementos z_{i j} serão dados pelo somatório das impedâncias mútuas entre as malhas i e j com o sinal trocado;
3. Como a matriz é SIMÉTRICA, os elementos z_{i j} = z_{j i};
4. Se duas malhas não possuem impedâncias em comum, o elemento da matriz correspondente será nulo.

Cada linha i da matriz V é composta pelo somatório das fontes de tensão da malha i, observando-se as seguintes polaridades:

• Fonte de tensão com corrente arbitrada entrando no pólo NEGATIVO da fonte: valor POSITIVO;
• Fonte de tensão com corrente arbitrada entrando no pólo POSITIVO da fonte: valor NEGATIVO.

Análise Sistemática do Exemplo 1

Vamos fazer o levantamento da matriz de impedâncias Z_2x2 e da matriz de fontes de tensão V_2x1.

Quais sejam:

E aí será possível resolver o sistema de equações no Scilab, da forma:

Em coordenadas polares:

Exemplo 2:

Seja o circuito abaixo e suas matrizes de impedância e fontes de tensão:

Análise Sistemática do Exemplo 2

A análise deste circuito no Scilab será:

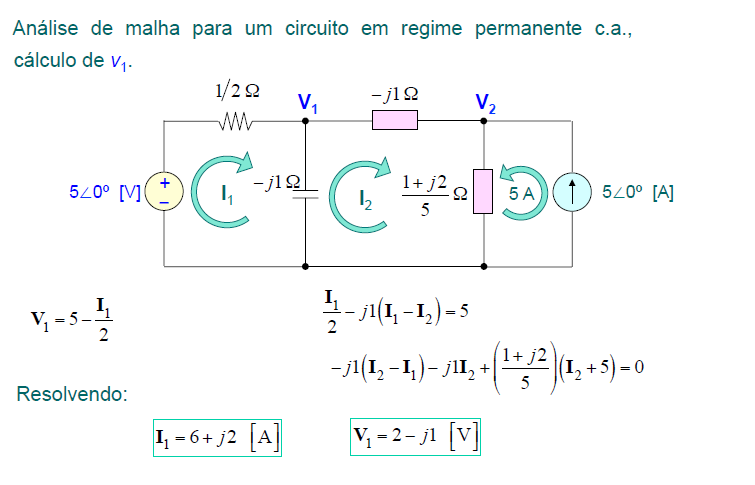
Exemplo 3:

Análise Sistemática do Exemplo 3

A análise sistemática deste circuito precisa considerar a fonte de corrente de 5A.

Basta incluir apenas as 2 equações das malhas 1 e 2, na matriz impedância, mas também uma terceira equação, que simplesmente relaciona a corrente da 3a. malha, com a fonte.

Qual seja:

                1. I3 = -5A

Assim, a matriz de impedâncias ficará:

Ou seja, a terceira linha, não será uma equação de tensão da forma Z _{x y} .I_x, como as demais equações. Esta equação, como se refere a uma fonte de corrente, incluirá apenas o valor da CORRENTE de malha, I₃, pois não é possível determinar-se a tensão nesta fonte.

Assim, torna-se possível resolver o sistema de equações no Scilab, da forma:

Note que a última equação, novamente, estabelece que I₃ = -5A, como esperado.

E a tensão V1 será:

Lei de Kirchoff para as correntes (KCL)

A soma das correntes em um nó é igual a zero.

Este método é o mais indicado quando N_nós < N_malhas do circuito!!!

Método de Análise simples

1. Identificar todos os N nós do circuito;
2. Arbitrar uma tensão V_n em cada nó;
3. Transformar todas as impedâncias do circuito em admitâncias: Y_k=1/Z_k;
4. Computar todas as correntes i_n, de todos os ramos que chegam ao nó, adicionando os elementos de circuito conectados ao nó desta forma:
   1. Fontes de tensão: adiciona uma variável/incógnita de corrente, porém já provê a tensão direta do nó: V_n = (+-)V_fonte, observada a polaridade;
   2. Admitância Y_n: corrente na admitância = (V_n - V_m).Y_n (ou como (V_n - V_m)/Z_n, se as impedâncias não foram transformadas em admitâncias); onde V_m é a tensão no nó adjacente do ramo, a qual entra no somatório com valor negativo, em relação à tensão do nó;
   3. Fontes de corrente: se a corrente da fonte chega no nó, ela entra com valor negativo no somatório, e positivo, caso contrário;
   4. Fontes dependentes: adiciona uma variável a determinar (+ uma equação).
5. Resolve o sistema de equações (matricial ou por substituição)

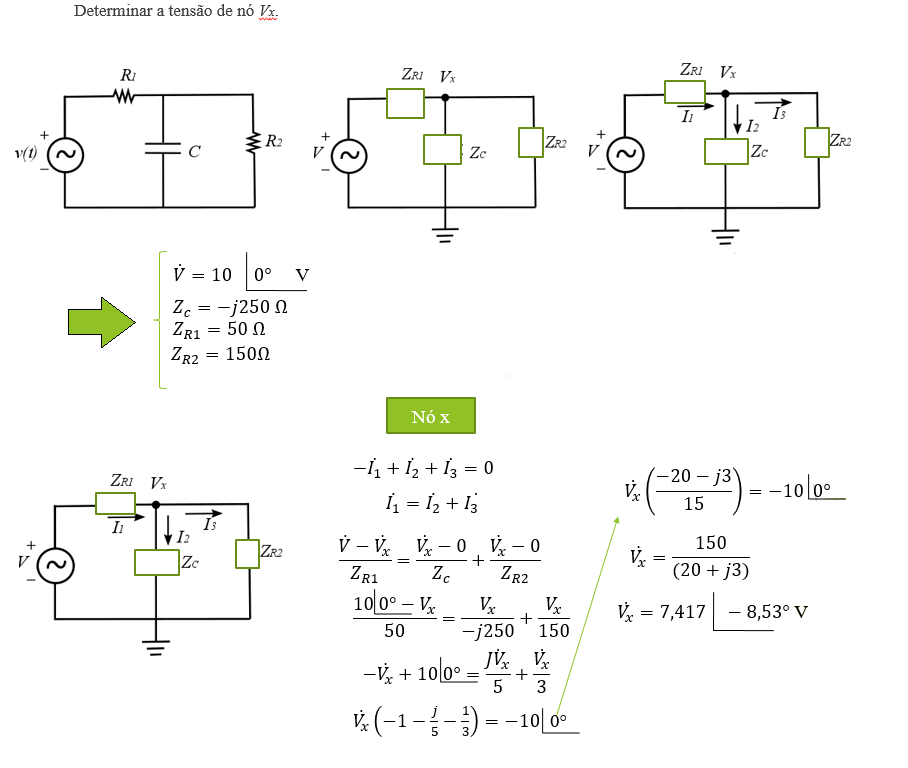
Exemplo 4:

Resolvendo pelo método simples:

Em valor eficaz. Ou V_x = 10,46 ∠ -8,53° V, de pico

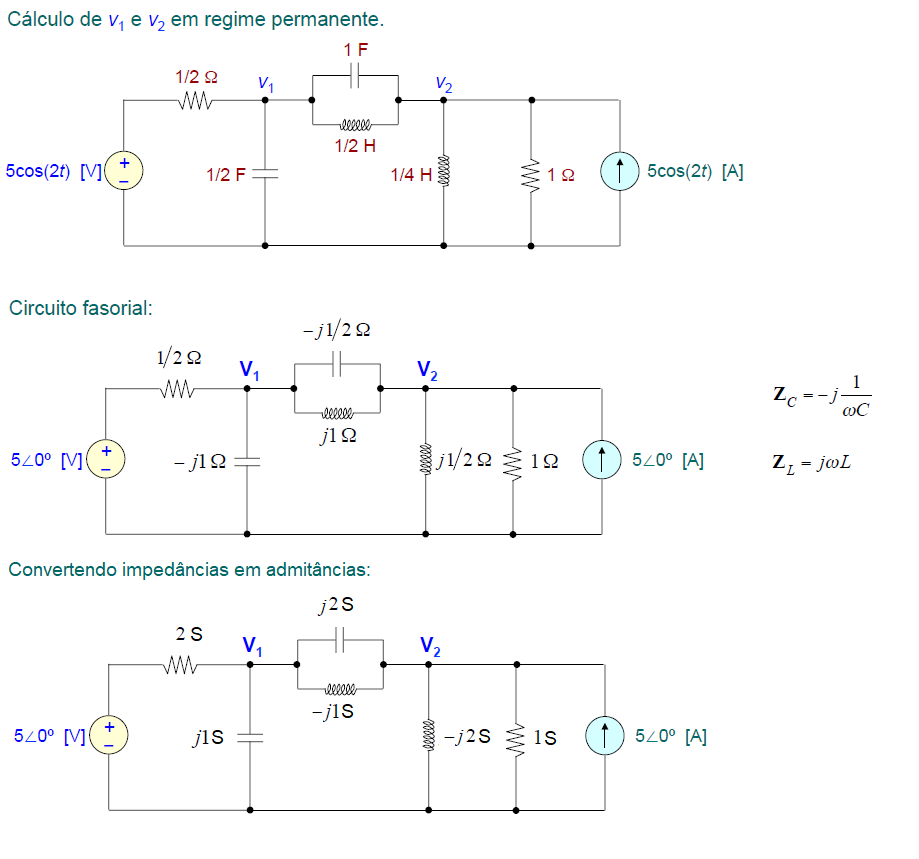
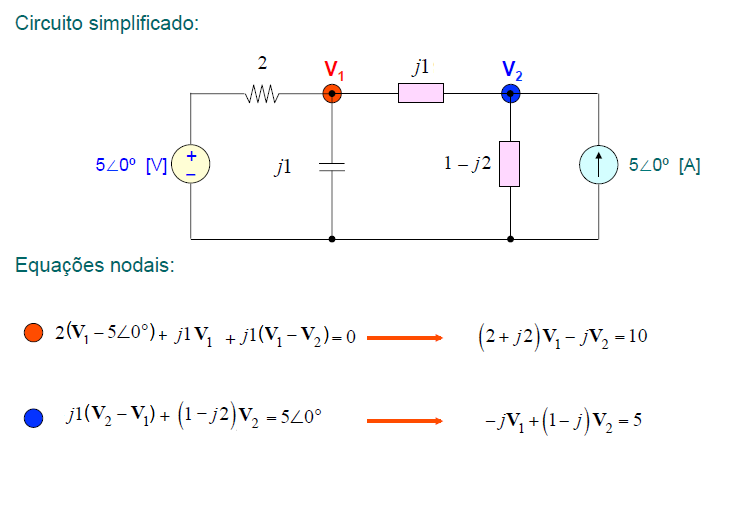
Exemplo 5:

O circuito abaixo tem 5 malhas, mas apenas 2 nós independentes (excetuando-se o nó de referência). Portanto, é mais fácil de analisar pelo Método dos Nós.

Resolvendo pelo método simples:

Método de Análise sistemática

A análise sistemática, que pode ser mais facilmente automatizada, consiste em organizar o sistema de equações do circuito na forma:

V = I.Y-1 

onde:

• I é a matriz coluna (N x 1), contendo os valores das fontes de correntes nos nós;
• Y é a matriz quadrada (N x N), contendo as admitâncias do circuito, e
• V é a matriz coluna (N x 1), contendo as tensões nos nós, que se quer determinar;

onde N é o número de nós independentes do circuito (excetuando-se a referência).

A partir disto, a solução do circuito consistirá em inverter computacionalmente a matriz de condutâncias Y, e multiplicá-la pela matriz de fontes de corrente I.

Assim, para cada nó i do circuito, contendo apenas fontes de corrente, a matriz Y será construída da seguinte forma:

1. Em cada posição da diagonal principal, os elementos y_{i i} serão dados pelo somatório de todas as admitâncias daquele nó i;
2. Os elementos y_{i j} serão dados pelo somatório das admitâncias mútuas entre os nós i e j com o sinal trocado;
3. Como a matriz é SIMÉTRICA, os elementos y_{i j} = y_{j i};
4. Se dois nós não possuem admitâncias em comum, o elemento da matriz correspondente será nulo.

Cada linha i da matriz V é composta pelo somatório das fontes de corrente ligadas ao nó i, observando-se as polaridades:

• Fonte de corrente com a corrente ENTRANDO no nó - valor positivo
• Fonte de corrente com a corrente SAINDO do nó - valor negativo

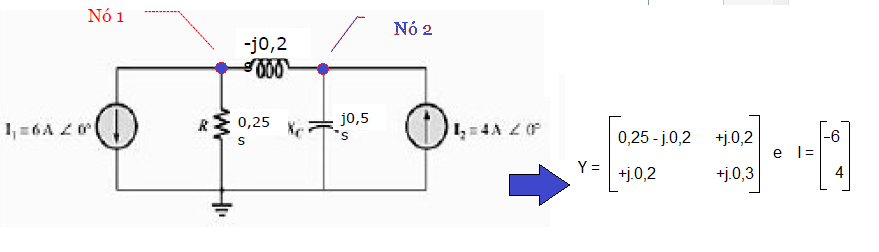
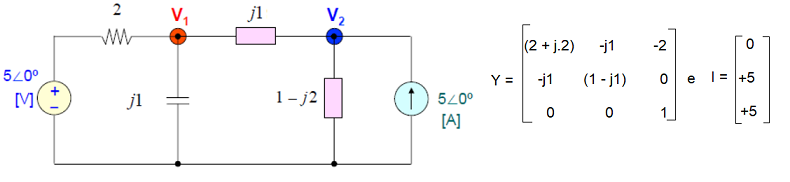
Exemplo 6

Seja o circuito com 2 nós abaixo, e suas matrizes de admitância Y e fontes de corrente I:

A análise sistemática no Scilab será:

Em coordenadas polares:

Exemplo 7

Seja o circuito abaixo e sua matriz de admitância. Como este circuito possui uma fonte de tensão, a matriz de fontes incluirá uma equação para tensão, e não apenas de correntes:

Como existe a fonte de tensão no circuito, devem ser incluídas apenas as equações dos nós que não têm fonte de tensão conectadas (no caso, apenas os nós 1 e 2) e a terceira equação, do que seria o nó 3 aonde está conectada a fonte de tensão, é tirada diretamente da relação:

1.V3 = 5V

e não das equações de corrente do tipo (Vx - Vy).Yxy.

A análise no Scilab será:

Confirmando os resultados obtidos pelo Método simples no Exemplo 5.

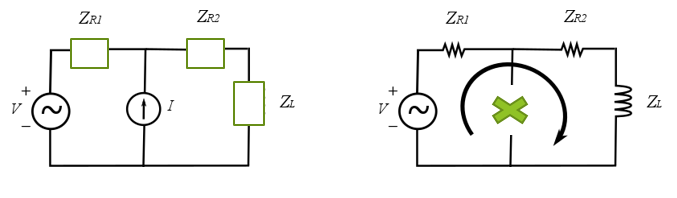
Supermalha

Adequada para circuitos que possuem malhas com fonte de corrente em comum. Consiste em excluir o ramo do elemento mútuo entre duas malhas, formando uma única super-malha, de forma a simplificar a análise de Malhas.

Exemplo 8:

Calcule a tensão V1 do circuito abaixo, utilizando exclusivamente ANÁLISE DE MALHAS:

Simulando no Scilab:

Ou seja, a corrente V1 no tempo será dada por:

   V1 = cos(2.t -36,87°) [V]

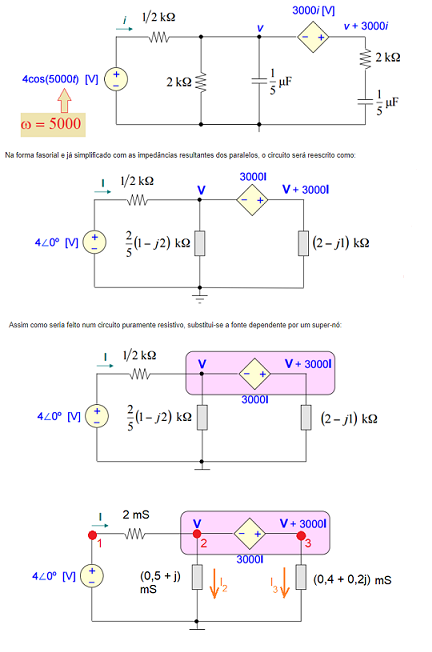
Supernó

Formado pela exclusão de uma fonte de tensão (dependente ou independente) conectada entre dois nós, com exceção do nó de referência, e qualquer elemento conectado em paralelo com ela.

Exemplo 9:

Calcule o valor da corrente I abaixo, usando exclusivamente ANÁLISE NODAL:

Simulando no Scilab:

Ou seja, a corrente I no tempo será dada por:

   I = 24. sen(5000.t + 53,13°) [mA]

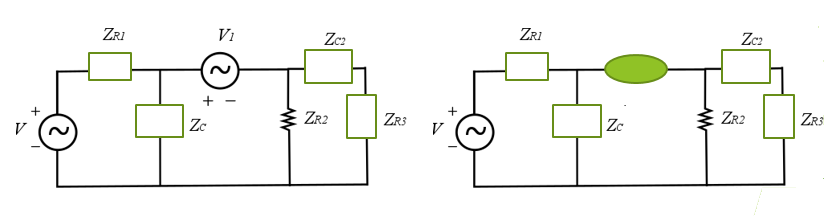
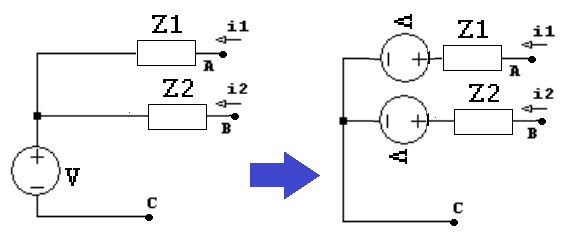
Teorema do deslocamento de fontes

Algumas vezes é interessante transformar uma fonte independente em muitas outras, pois isto pode simplificar a análise do restante do circuito.

Quando isto é feito chamamos de explosão, transformação (pode ser usado com outro significado) ou deslocamento de fontes.

Uma fonte de tensão independente que tenha um de seus terminais ligados a mais de um elemento de circuito pode ser desmembrada removendo este nó, desde que cada elemento permaneça interligado em série com uma fonte de tensão de mesmo valor e polaridade.

A figura a seguir ilustra o fato.

Do ponto de vista do resto do circuito as formas de onda de tensão e corrente nos terminais A, B e C permanecem inalteradas.

• Deslocamentos podem ser feitos também com fontes controladas, mas é preciso ter cuidado com modificações nas variáveis controladoras das fontes, quando fontes são deslocadas para os ramos que as contém
• Como cada deslocamento elimina um nó do circuito, o máximo número de fontes de tensão em um circuito é igual ao número de nós, exceto o nó de terra
• Estes deslocamentos não afetam as correntes nos ramos.

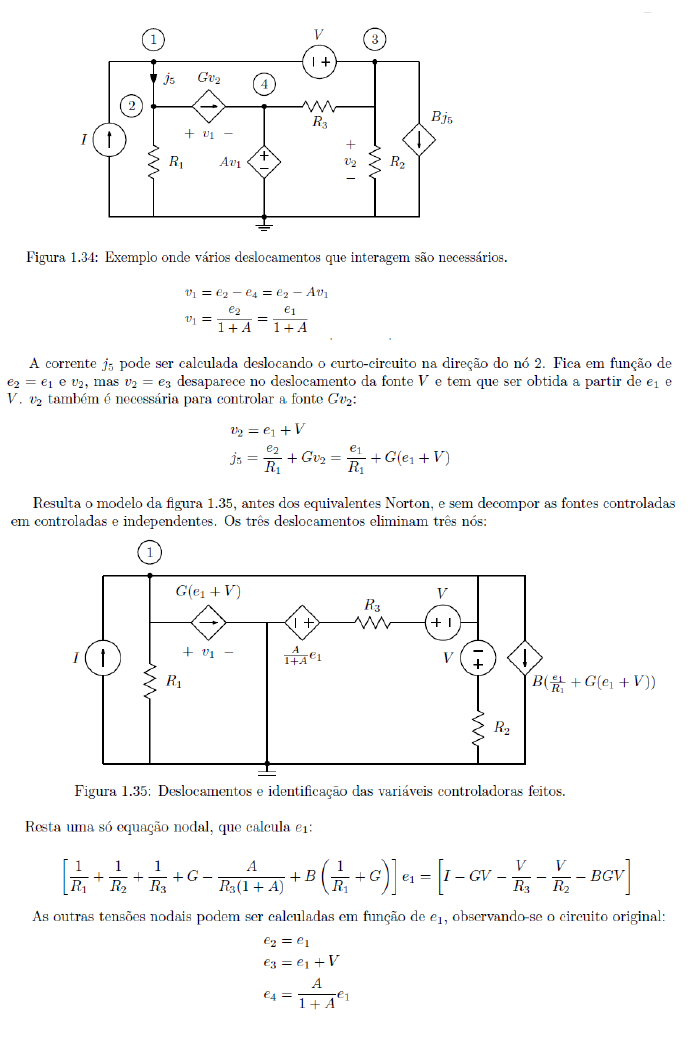
Exemplo:

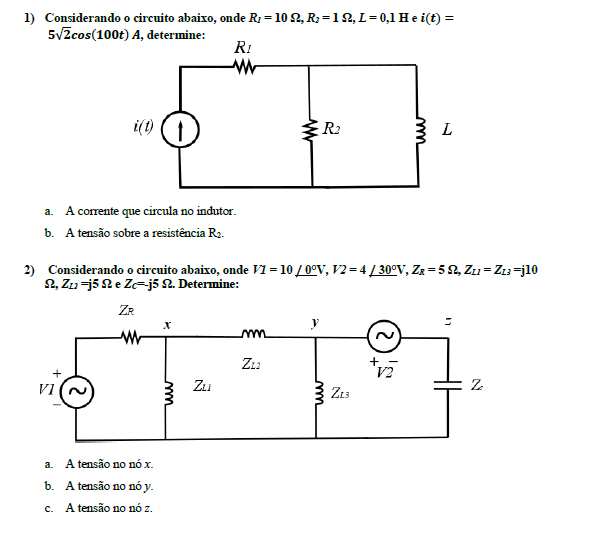
Exercícios

Resolução Exercícios 1 e 2

Resolução Exercícios 3 e 4

5) Resolva o circuito do exemplo 8 por meio da Análise Nodal sistemática.

6) Resolva o circuito do exemplo 9 por meio de Análise de Malhas sistemática.

7) Resolva os circuitos anteriores pelos métodos de análise de Kirchoff.

Bibliografia

[1] SADIKU, M. N. O.; MUSA, S. M.; ALEXANDER, W. K. Análise de Circuitos Elétricos com Aplicações. Porto Alegre: Mc Graw Hill Education, 2014. v. 3.

[2] BOYLESTAD, R. L. Introdução à Análise de Circuitos. 12a ed. São Paulo: Pearson, 2011.

[3] PETRY, C. Circuitos 2. Disponível em: Aula 4 - Impedância e Reatância, 2023.

[4] BALDINI Fo., Renato. EA-513 Circuitos Elétricos, Notas de Aula, Disponível em: Circuitos Elétricos, 2014.

---

<< Página do curso

<< Reatâncias e Impedâncias	Lei de Ohm, Divisor de corrente/tensão e Leis de Kirchoff em CA, RP	Equivalentes de Thevénin e Norton, RP >>