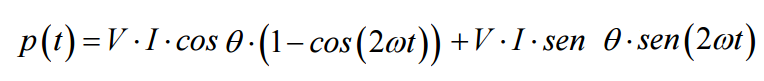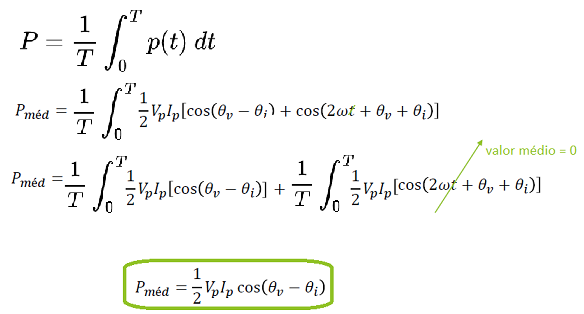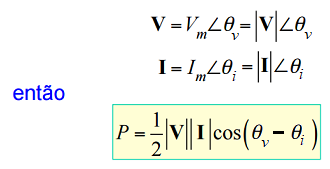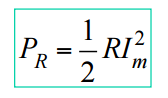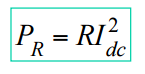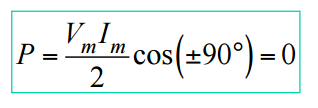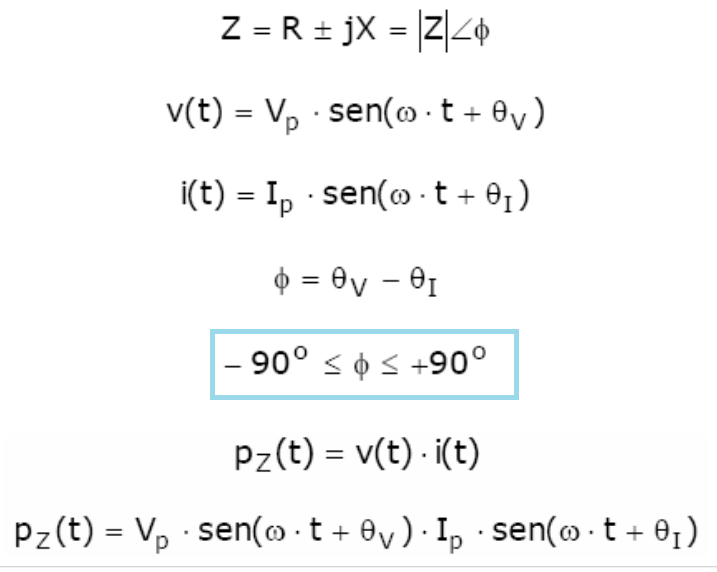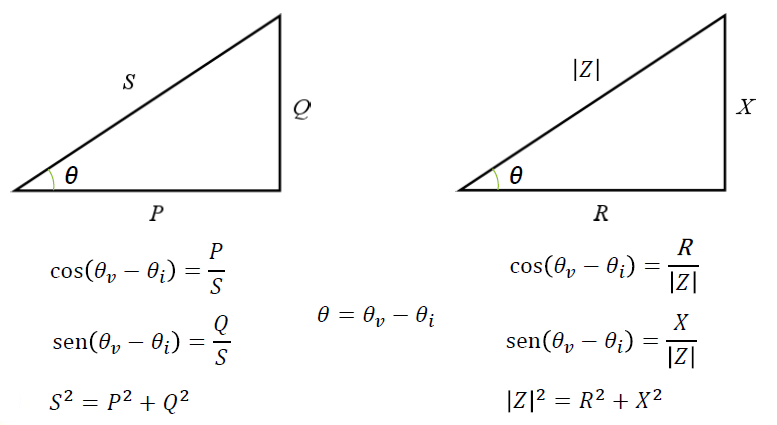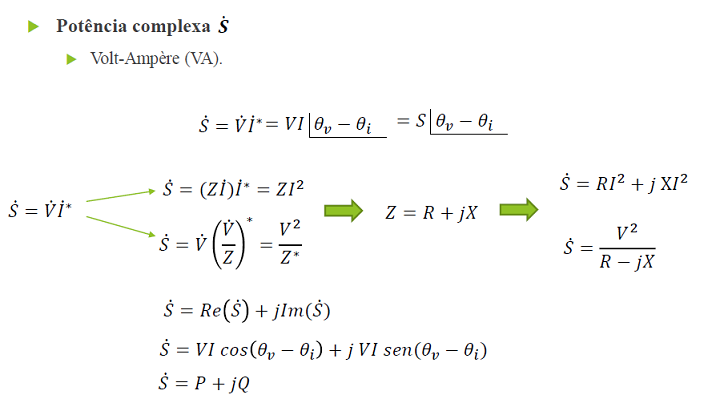AULA 8 - Circuitos Elétricos 2 - Graduação
Análise de potência CA
Entende-se por Potência Elétrica, a capacidade de um consumidor de produzir trabalho em um determinado tempo, a partir da energia elétrica produzida e entregue.
Em um circuito de corrente contínua, a potência é dada em watts, multiplicando-se simplesmente a tensão pela corrente.
Todavia, quando se trata de circuitos de CA com cargas indutivas e/ou capacitivas, ocorre uma defasagem entre tensão e corrente. Isso nos leva a considerar três tipos de potência:
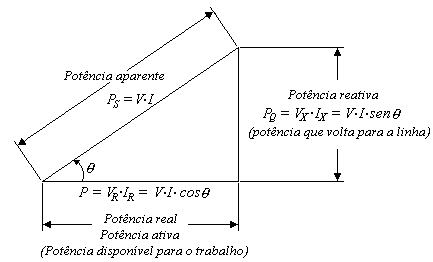
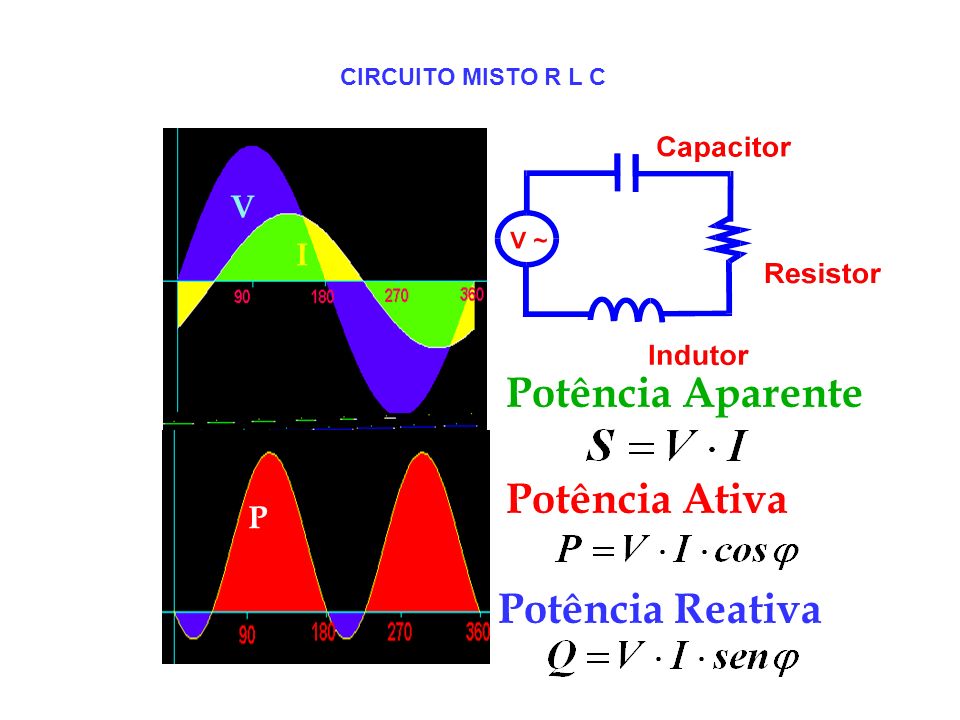
- Potência Aparente (S)
- Potência Ativa (P)
- Potência Reativa (Q)
Vejamos na sequência, as bases teóricas para este estudo:
Potência instantânea
É a Potência absorvida por um elemento em um dado instante de tempo.
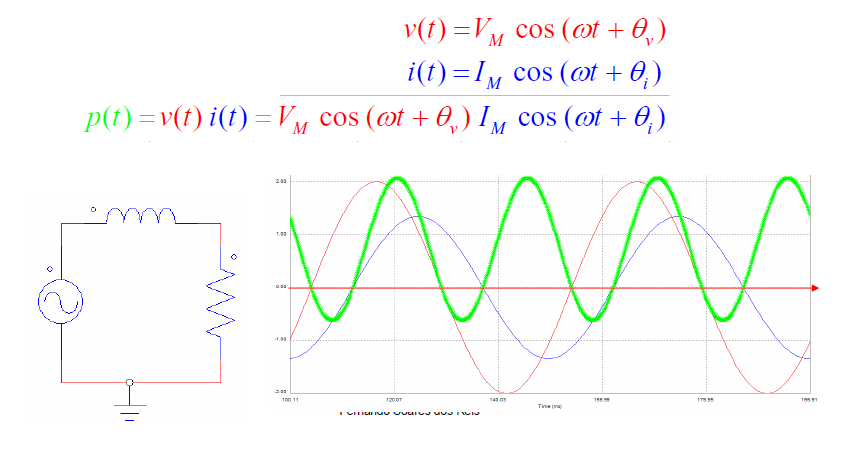
Será dada por:
, isto é, a potência instantânea será composta por um termo constante no tempo:
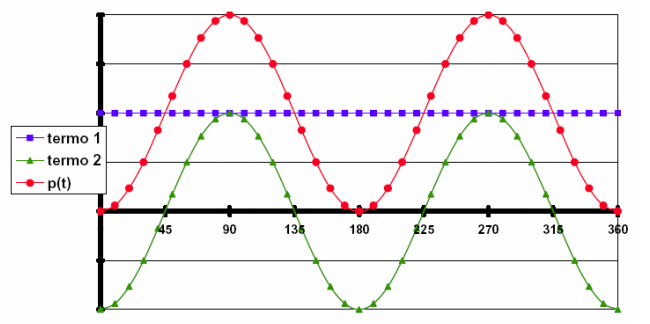
termo 1 = 1/2. Vp. Ip. cos (θv - θi)
e por um termo variável, função do tempo:
termo 2 = 1/2. Vp. Ip. cos (2.ωt + θv + θi) )
Graficamente:
Situações especiais
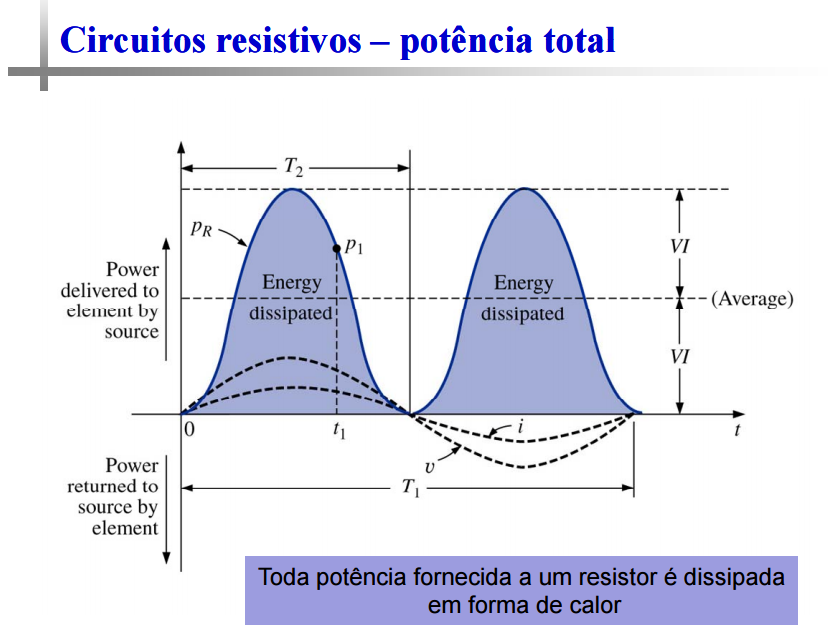
Na primeira situação: I2= I ‧ I*. A equação demonstra que um circuito puramente resistivo absorve potência o tempo todo.
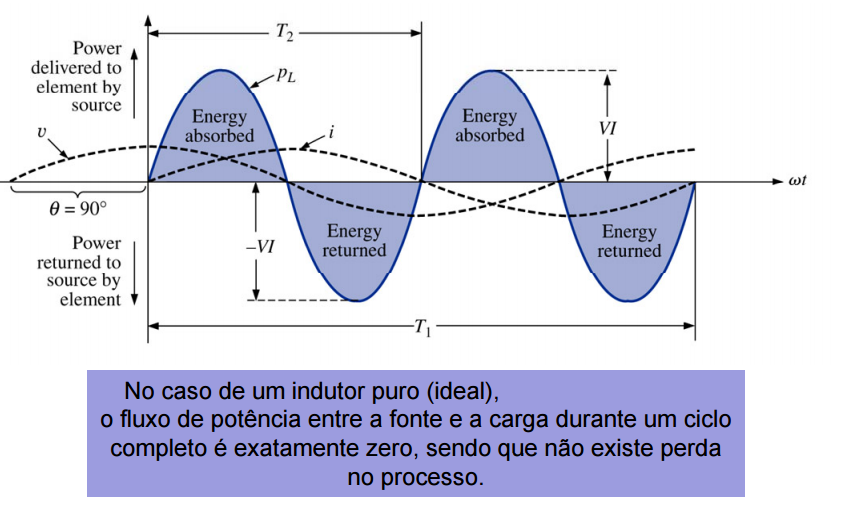
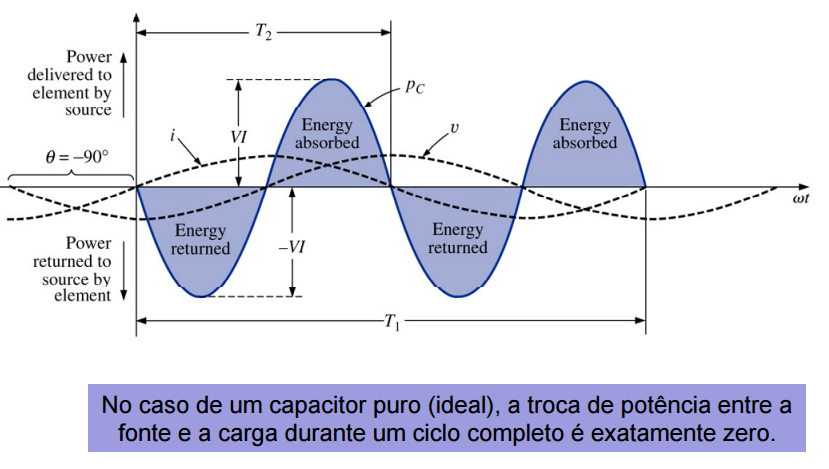
Já na segunda situação, a equação mostra que um circuito puramente reativo (ou seja, formado por L ou C) não absorve nenhuma potência média.
Pelo valor do ângulo de fase θ = (θv - θi) podemos inferir:
Assim, quando θ = (θv - θi) = 0:
E, quando θ = (θv - θi) > 0:
E, por fim, quando θ = (θv - θi) < 0:
Potência instantânea no circuito misto
Assim como no circuito resistivo, haverá gasto energético (consumo de energia).
A potência instantânea terá que ser calculada em função dos valores de fase θv e θi da tensão e corrente em cada um dos elementos (impedâncias).
A potência instantânea, então, varia muito em circuitos CA.
Ela pode ser decomposta em três componentes da potência elétrica: potências aparente, ativa e reativa.
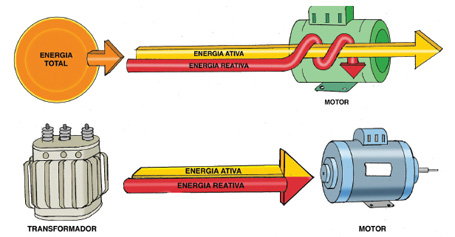
- A potência ATIVA, ou Média, é a que realiza Trabalho, de fato. Unidade é o Watt (W).
- A potência REATIVA é aquela potência consumida por reatâncias (indutivas ou capacitivas) no armazenamento de energia, magnética ou elétrica, para o devido funcionamento do sistema elétrico. Unidade é o Volt-Ampère reativo (var).
- A potência APARENTE é a potência total fornecida pela fonte. Unidade é o Volt-Ampère (VA).
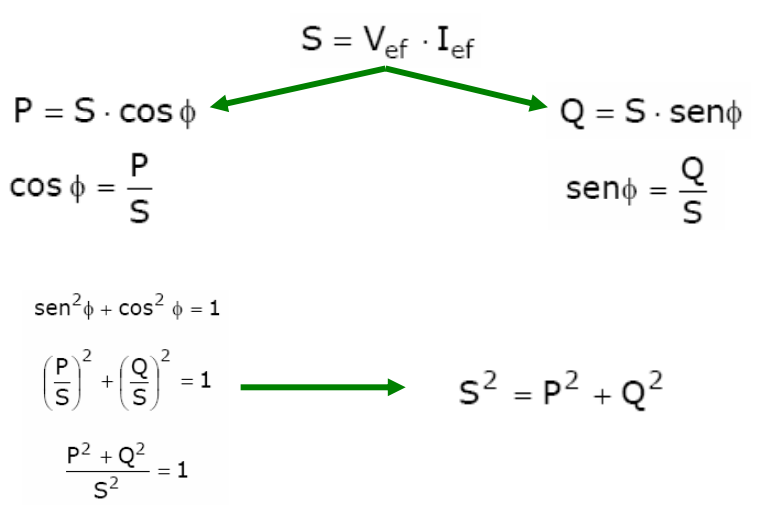
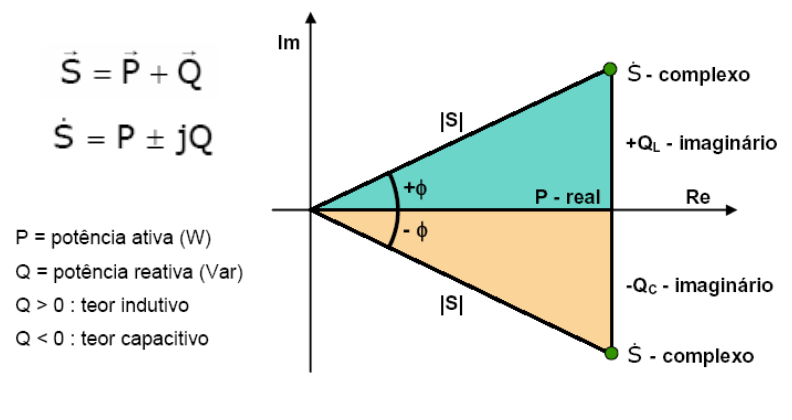
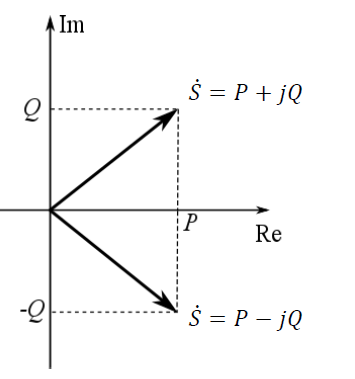
A potência Aparente é calculada pela soma vetorial dos fasores de potências ativa e reativa:
Assim, conhecendo pelo menos duas grandezas dentre S, P, Q e fator de potência, é possível determinar as grandezas restantes utilizando trigonometria.
No caso da Potência Reativa, existe a dualidade entre os tipos de reatância, daí ser atribuído o sinal positivo à Potência reativa Indutiva e o negativo, à Potência reativa Capacitiva.
Entre essas potências existe uma relação conhecida como fator de potência (FP), determinada pelo cosseno do ângulo entre a potência ativa e a aparente, ou seja, P/S ou o cosseno do ângulo de fase, entre a tensão e a corrente.
Exemplo 18
Dados v(t) e i(t): 
, calcule a potência instantânea e qual o tipo de carga:
Resolução:
p(t) = v(t).i(t)
p(t) = 127.cos(377t + 30º ) × 5.cos(377t - 5º)
p(t) = 653.cos(377t + 30º ).cos(377t - 5º)
Aplicando-se a identidade trigonométrica cos(a).cos(b) = 0,5.[cos(a + b) + cos(a - b)]:
p(t) = 317,5.[ cos(377t + 30º + 377t - 5º) + cos(377t + 30º - 377t + 5º)]
⇒ p(t) = 317,5.[ cos(754t + 25º) + cos(35º)]
Como o ângulo θ = 35º e, portanto, 0 < θ < 90º pode-se inferir que a fonte alimenta uma carga RL!
Potência média
A Potência Média, ou POTÊNCIA ATIVA está relacionada à geração de calor, movimento ou luz.
Basicamente, ela pode ser considerada como a média da potência elétrica gerada por um único dispositivo com dois terminais.
É resultado do gasto energético após o início de cada processo de transmissão de energia, como o da corrente elétrica até os equipamentos que temos em casa, ou mesmo em máquinas industriais.
A potência ativa, que pode ser medida em watts (W) ou kilowatts (KW), por meio de um aparelho chamado wattimetro, é a energia que será realmente utilizada.
Será dada por:
Uma vez que* : 
* Para maiores informações, vide: Breve revisão de relações trigonométricas
Exemplo 19
Dado que v(t) e i(t):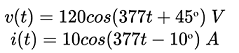 
, calcule a potência instantânea, o tipo de carga alimentada pelo circuito e a potência média (ativa):
p(t) = 120.cos(377t + 45º ) × 10.cos(377t - 10º)
p(t) = 1200.cos(377t + 45º ).cos(377t - 10º)
p(t) = 600.[ cos(754t + 35º) + cos(55º)]
⇒ p(t) = 600.[ cos(754t + 35º)+ cos(55º)]
Como o ângulo θ = 55º e, portanto, 0 < θ < 90º pode-se inferir que a fonte alimenta uma carga RL!
Já a potência média será:
Pmed = ½ Vp.Ip.cos(θv - θi)
Pmed = ½ 120.10.cos(45º - (-10º))
⇒ Pmed = 600.cos(55º) = 344,2 W
Exemplo 20:
A potência ativa pode ser vista, também, como a parte real da potência entregue à carga:
Em termos de fasores:
Potência ativa no resistor
Se a carga é um resistor, então θ = 0 e Vm = R.Im, assim:
Note que se i = Icc (corrente constante), então ω = θ = 0º e Im = Icc, então,
Potência ativa no indutor e no capacitor
- Se o bipolo é um indutor, então θ = 90°.
- Se o bipolo é um capacitor, então θ = -90°.
Assim, para ambos os casos, temos:
Potência Reativa
Como já vimos, a potência instantânea é dada por:
Em um circuito misto, que contenha resistências e reatâncias indutivas e capacitivas:
A potência reativa, por sua vez, não realiza o trabalho em si.
Isso significa que não é essa energia que liga os eletroeletrônicos e outros equipamentos elétricos, mas ela funciona entre o gerador de energia e a carga em si, sendo responsável por manter o campo eletromagnético ativo em motores, reatores, transformadores, lâmpadas fluorescentes, etc.
Em outras palavras, é a potência usada apenas para criar e manter os campos eletromagnéticos das cargas indutivas ou capacitivas.
Sua medida é feita em VAR, que significa volts-Amperes-Reativos.
Numa instalação elétrica que apenas possua potência reativa, a potência ativa média tem um valor nulo, pelo que não é produzido nenhum trabalho útil. Diz-se portanto que a potência reativa é uma potência devatada (não produz watts ativos).
Na indústria elétrica, recomenda-se que todas as instalações tenham um fator de potência máximo, que fará a parcela V.I.sen(φ) da potência reativa, não-útil, portanto, ser mínima.
Assim, enquanto a potência ativa é sempre consumida na execução de trabalho, a potência reativa, além de não produzir trabalho, circula entre a carga e a fonte de alimentação, ocupando um espaço no sistema elétrico que poderia ser utilizado para fornecer mais energia ativa.
A integração temporal da potência reativa resulta numa energia reativa, que representa a energia que circula de forma oscilante nas instalações, mas não é consumida por nenhum receptor.
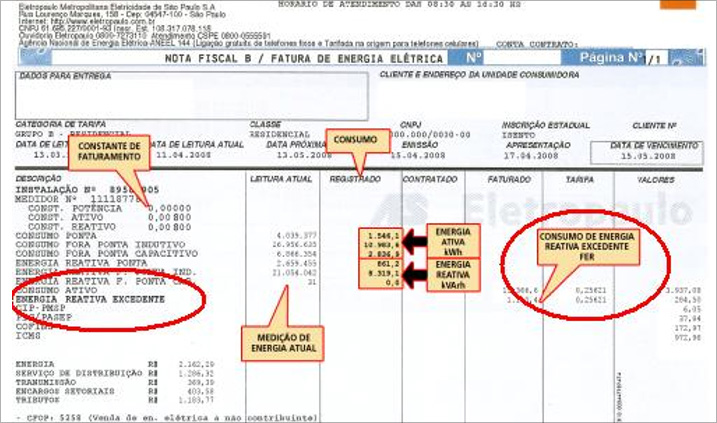
Em casos de consumidores especiais de energia elétrica (grandes consumidores), esta energia pode ser contabilizada em VAr-hora, e faturada adicionalmente à energia ativa consumida.
Potência Aparente
Definição:
É o produto da tensão pela corrente (eficazes)
Também pode ser definida como a soma vetorial das potências ativa e reativa.
As relações matemáticas entre os três tipos de potência podem ser resumidos por:
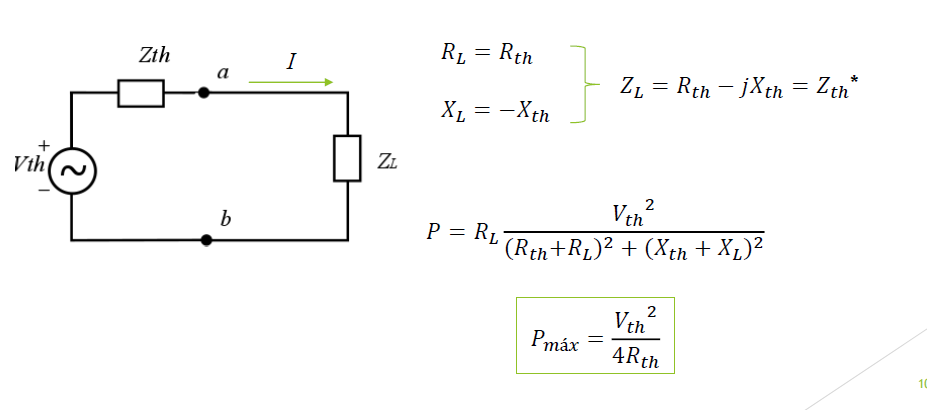
Máxima Transferência de Potência
"A máxima transferência de potência vai acontecer quando a impedância da carga for casada (igual ao complexo conjugado) à impedância de Thevenin equivalente da fonte."
Isto é:
ZL = ZTh*
ou:
E, portanto, a potência máxima será:
P = VTh2/(4.RTh)
porque, como visto, as reatâncias não executam trabalho.
Demonstração
Sabemos que o máximo acontece na curva quando a derivada é zero. Então, para a resistência:
E para as reatâncias:
Princípio da CONSERVAÇÃO da energia/potência
"As potências complexa, ativa e reativa de uma fonte são iguais à soma das respectivas potências complexas, ativas e reativas das cargas individuais."
Resumo
Exercícios
1)
RESOLUÇÃO:
2) Uma determinada impedância, alimentada por tensão de 220V, consome uma potência de 9KW e cos φ = 0,8. Determine:
a) corrente de entrada da resistência;
b) Potência aparente;
c) Potência reativa
Resposta: Exercício 1 - Cap.11
3) Um gerador de 100 V eficazes e 60 Hz alimenta o seguinte conjunto de cargas:
3.1) Um motor de indução de 1,5 kVA e 1,2 kW.
3.2) Dez lâmpadas fluorescentes de 60 W cada uma, cos θ = 0,6 em atraso.
Determine:
a) As potências ativa, reativa e aparente fornecidas pelo gerador.
b) O fator de potência da instalação, isto é, do conjunto de cargas.
c) Um bipolo (e tipo) que conectado em paralelo corrige o fator de potência.
Resposta: Exercício 3 - Cap.11
4) Um gerador de 100 V eficazes e 60 Hz alimenta as seguintes cargas em paralelo:
4.1) Dez lâmpadas fluorescentes de 60 W cada uma, θ cos = 0,6 em atraso.
4.2) Uma carga de impedância Z = (6 + 12 j)Ω .
4.3) Um motor de indução de 1,2 kW e 2 kVA.
Determine:
a) As potências ativa, reativa e aparente fornecidas pelo gerador.
b) O fator de potência da instalação elétrica (isto é, do conjunto de cargas).
c) Os valores dos capacitores que conectados em paralelo com as cargas transformam o fator de potência em 0,9 (adiantado e atrasado).
d) Qual é a redução porcentual da corrente fornecida pelo gerador após a correção do fator de potência?
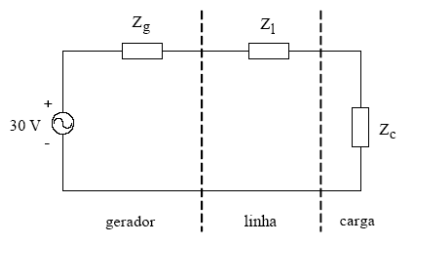
5) Um gerador senoidal de força eletromotriz de 30 V eficazes e impedância interna Zg = (2 + 3 j)Ω alimenta uma carga linear através de uma linha de impedância Zl = (6 + 2j)Ω , como mostra a figura. A carga Zc = (8 − 5j)Ω dissipa a máxima potência ativa.
Determine:
a) As potências ativa, reativa, aparente e o fator de potência na linha.
b) O fator de potência da carga Zc
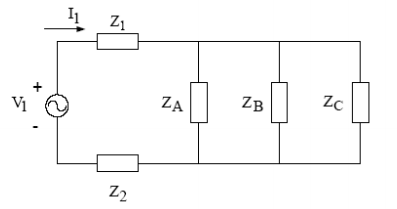
6) A tensão nos terminais das cargas A, B e C é de 2300 V. As três cargas são descritas como segue:
A: 10 kW e fator de potência de 0,707 atrasado.
B: 10 kVA e fator de potência de 0,9 adiantado.
C: 18 kW e fator de potência de 0,6 atrasado.
Se Z1=Z2=(4+2j) Ω, determine a tensão, a corrente, o fator de potência e a potência fornecida pela fonte.
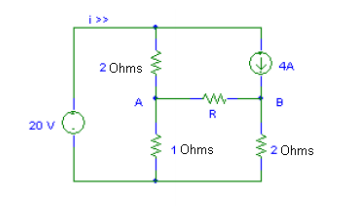
7) Obtenha o equivalente de Thévenin entre os pontos A e B para o circuito abaixo: Calcule o valor de i para os seguintes casos:
a) R = 2 ohms b) R = 5 ohms c) R = 0
Lista de Exercícios do Irwin:
1) Em um determinado componente, a tensão instantânea é v(t) = 6.cos(ω.t) e a corrente é i(t) = 4.sen(ω.t). Qual a potência média no componente? Resposta: 0 W
2) Em um determinado componente, a tensão instantânea é v(t) = 170.cos(ω.t + 30°) e a corrente é i(t) = 5.cos(ω.t + 45°). Qual a potência média no componente? Resposta: 410,52 W
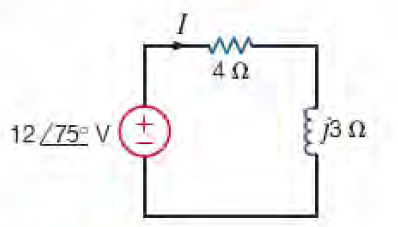
3) Qual a potência instantânea fornecida pela fonte?
Resposta: p(t) = 11,52 + 14,4.cos(2.ω.t + 113,13°) [W]
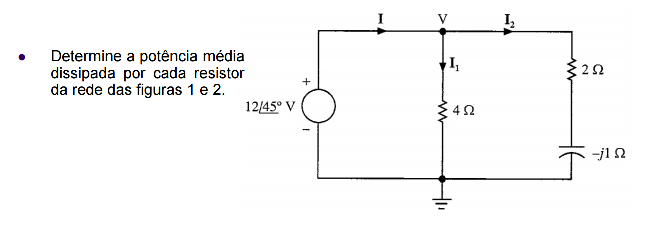
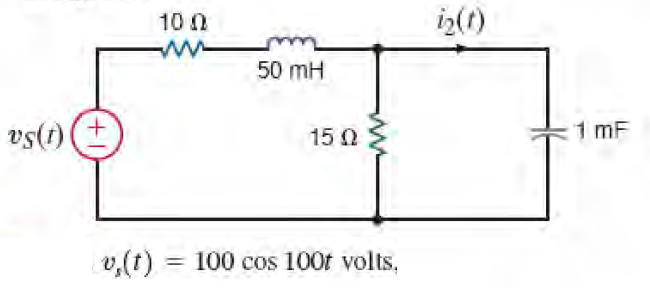
4) Qual a potência média fornecida pela fonte e o valor de I2?
Resposta: P = 336,11 W e I2 = 5,64 <41,18°
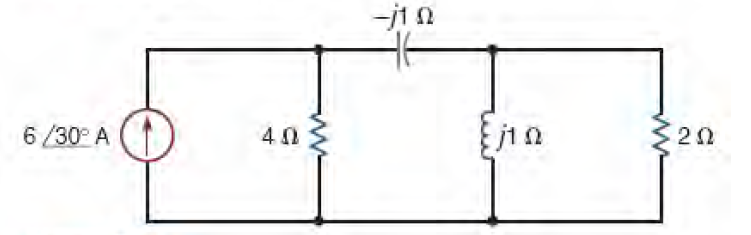
5) Qual a potência instantânea fornecida pela fonte?
Resposta: p(t) = 7,31.[0,914 + cos(2.ω.t + 36,04°] [W]
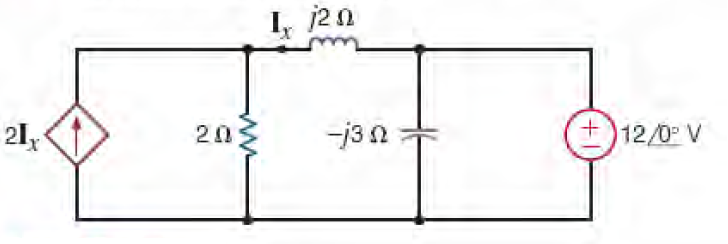
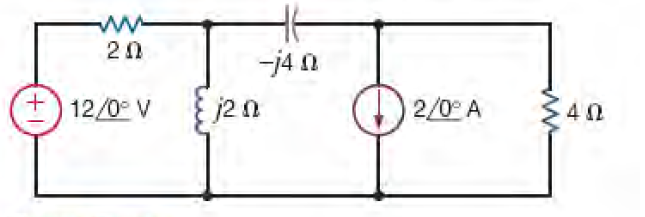
6) Qual a potência média absorvida pelo resistor de 2 Ω?
Resposta: P2Ω = 32,38 W
7) Qual a potência média absorvida pelo resistor de 4 Ω?
Resposta: P4Ω = 9,42 W
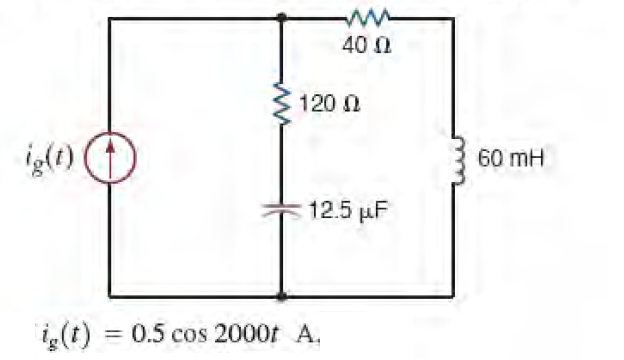
8) Qual a potência média absorvida por cada componente do circuito abaixo?
Resposta: Pfonte = 9,98 W, P120Ω = 7,48 W, P40Ω = 2,49 W, PC = 0 W, PL = 0 W.
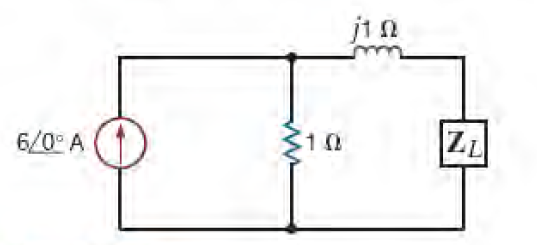
9) Determine o valor de ZL para máxima transferência de potência.
Resposta: ZL = ZTh = (1 - j) Ω para Pmáx = 4,5 W
Bibliografia
[1] SADIKU, M. N. O.; MUSA, S. M.; ALEXANDER, W. K. Análise de Circuitos Elétricos com Aplicações. Porto Alegre: Mc Graw Hill Education, 2014. v. 3.
[2] BOYLESTAD, R. L. Introdução à Análise de Circuitos. 12a ed. São Paulo: Pearson, 2011.
[3] PETRY, C. Circuitos 2. Disponível em: Aula 11 - Potência em CA regime permanente, 2023.
[4] BALDINI Fo., Renato. EA-513 Circuitos Elétricos, Notas de Aula, Disponível em: Circuitos Elétricos, 2014.
| << Simulação e Solução Computacional | Potência CA | Fator de potência >> |
|---|