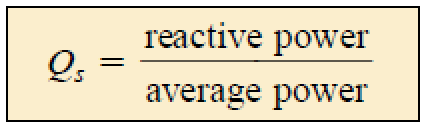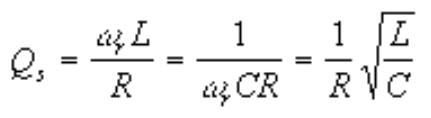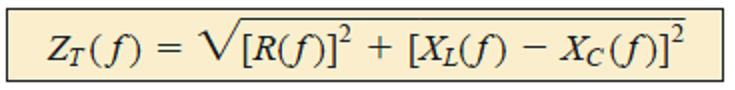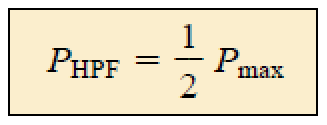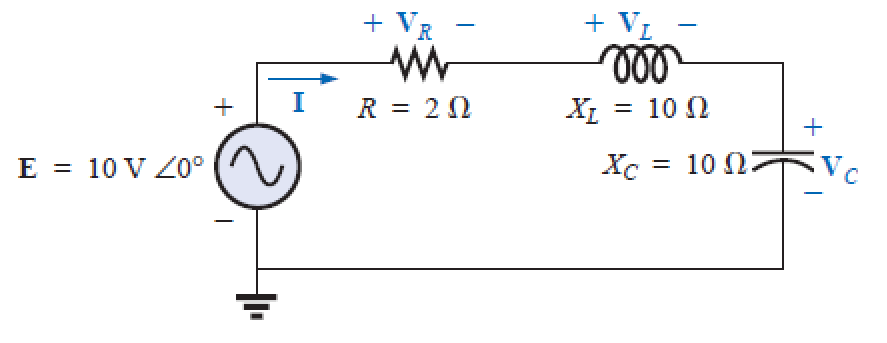AULA 10 - Circuitos Elétricos 2 - Graduação

RESSONÂNCIA

Circuito ressonante é uma combinação de elementos R, L e C que possui uma resposta em frequência que tem valor igual ou próximo do máximo em uma dada faixa de frequência.

Por sua vez, Resposta em frequência é a variação da amplitude do sinal senoidal em função da frequência:

Quando o circuito está próximo do máximo, diz-se que está em ressonância.

A ressonância é um efeito físico muito utilizado em sistemas elétricos e eletrônicos (filtros, seleção de frequências em redes de comunicação) e sistemas mecânicos (oscilações, vibrações), etc.

Frequência de ressonância

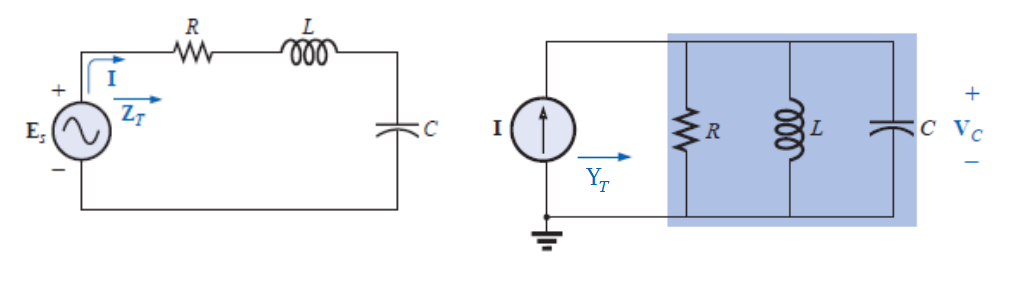
Sejam os circuitos mostrados na figura abaixo:

A impedância de entrada Z do circuito série é:

Z(jω) = R + jωL + 1/(jωC) 
              = R + jωL - j/(ωC)

e a admitância Y do circuito paralelo é:

Y(jω) = G + jωC + 1/(jωL) 
              = G + jωC - j/(ωL)

Note que ambas as equações possuem a mesma forma geral.

Os termos imaginários em ambas as equações serão nulos se:

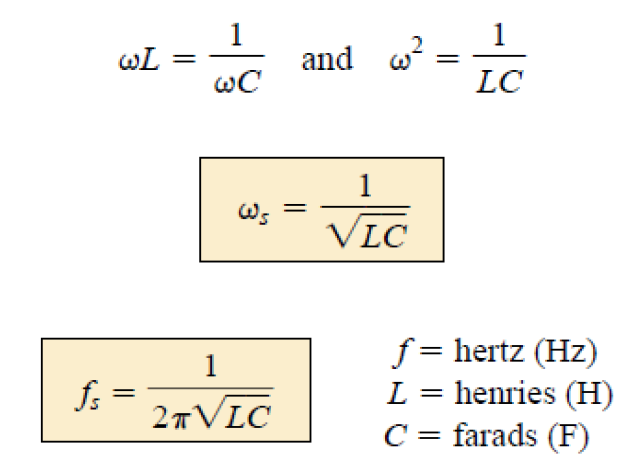
 ωL = 1/(ωC)

O valor de ω que satisfaz esta equação é:

e com este valor, as impedância e admitância dos circuitos vão se resumir a:

 Z(jω) = R

e

Y(jω) = G

Esta frequência ωs que torna a impedância de um circuito RLC real chama-se frequência de ressonância ou frequência natural, e os circuitos que operam na mesma são chamados circuitos ressonantes.

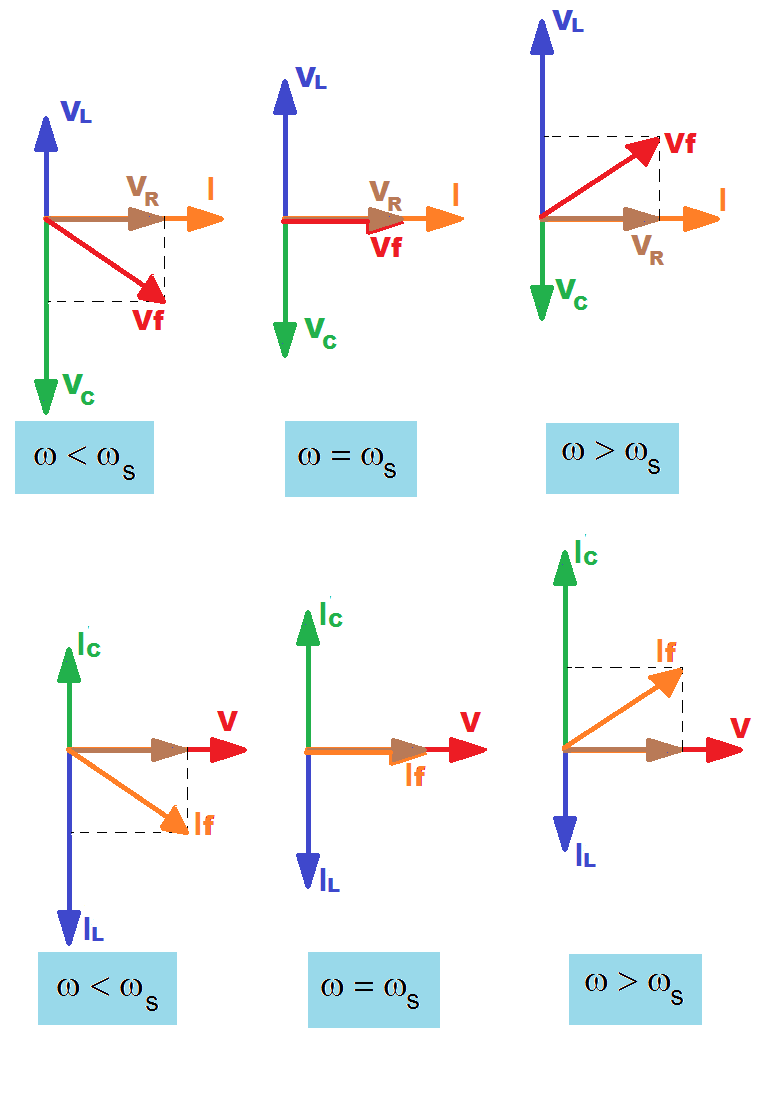
A ressonância pode ser vista sob outra perspectiva - a fasorial.

No circuito RLC série, a corrente é comum a todos os elementos, e no circuito paralelo, a tensão é a variável comum.

Portanto, estes parâmetros são utilizados como referência, nos gráficos abaixo:

Circuitos ressonantes

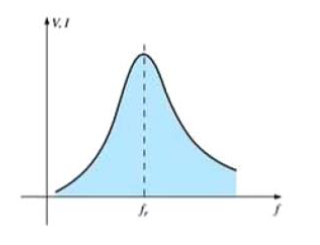
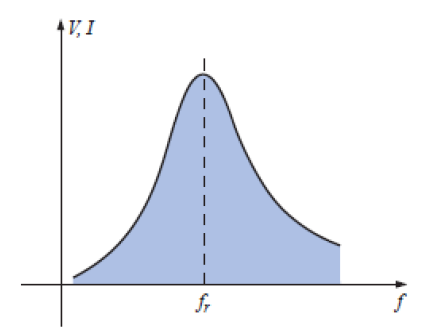
Circuito Ressonante (ou sintonizado), portanto, é o circuito em que a combinação de elementos R, L e C gera uma resposta em frequência semelhante a da figura abaixo.

Observa-se na figura que a resposta é máxima para a frequência fs.

Em fins práticos, para uma determinada faixa de frequência, a resposta tem valor igual ou próximo do valor máximo. Em frequências distantes, sua influência no sistema é menor.

A ressonância é um conceito muito importante em engenharia e não está limitada aos fenômenos elétricos, mas também mecânicos e magnéticos. Um caso muito célebre foi o da queda da ponte Tacoma

Os circuitos ressonantes são encontrados em praticamente todos os equipamentos de telecomunicações. Eles são responsáveis pela:

• frequência do sinal que deve ser transmitido ou recebido (portadora),
• pela separação de sinais em filtros,
• pela rejeição de interferências e ruídos e muito mais.

Todos os objetos possuem uma freqüência própria de vibração, a freqüência de ressonância.

Percebemos isto quando batemos numa taça, num pedaço de metal ou num diapasão. O material de que é feito o objeto, suas dimensões e seu formato determinam esta freqüência.

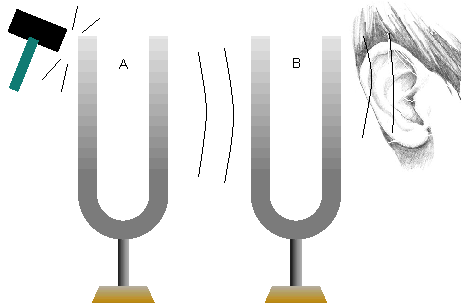
Um fato interessante pode ser observado quando dois objetos próximos têm a mesma freqüência de ressonância e fazemos um deles vibrar. Dois diapasões afinados para a mesma freqüência, por exemplo, podem servir de exemplo. Quando batemos em um emitindo um som, este som faz com que o outro diapasão entre em vibração.

Podemos perceber isto aproximando o ouvido do segundo diapasão, conforme mostra a figura.

Este fenômeno também ocorre com os circuitos eletrônicos. Determinados circuitos eletrônicos também possuem frequências próprias de vibração, emitindo sinais numa única freqüência quando são excitados.

E, circuitos RLC ressonantes que sejam alimentados por estas frequências tendem a vibrar de forma mais intensa, em um frequência única!

Como isto funciona?

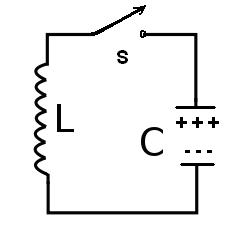
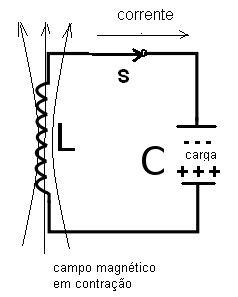
Assim, tomando o circuito básico da figura abaixo, vamos supor que o capacitor esteja completamente carregado.

Nestas condições iniciais, existe um campo elétrico uniforme entre as armaduras do capacitor e nele está armazenada a energia do circuito.

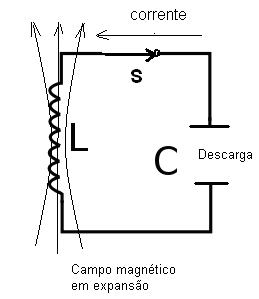
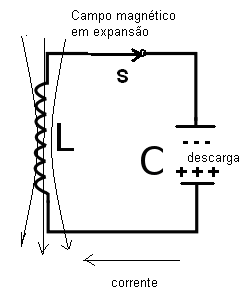
Fechando o interruptor, uma corrente de descarga do capacitor flui através do indutor. Com a descarga do capacitor a corrente criada cria um campo magnético que se expande para o qual é transferida a energia, conforme mostra a figura:

Quando a corrente de descarga cessa, toda a energia está no campo magnético do indutor. Neste momento, o campo magnético começa a contrair-se induzindo no indutor uma tensão que carrega o capacitor, mas com polaridade oposta, conforme mostra a figura:

Terminada a contração do campo, com o seu desaparecimento, o capacitor começa agora a descarregar-se novamente, mas com uma corrente oposta à inicial. Esta corrente gera um novo campo magnético invertido que se expande no indutor, conforme mostra a figura 6.

Novamente, com a descarga completa do capacitor e o campo magnético no máximo, inicia-se uma nova contração com uma nova carga do capacitor com a polaridade original. Um novo ciclo como o descrito tem então início.

Se a carga e descarga do capacitor não ocorresse com perdas o ciclo ocorreria por tempo infinito, gerando assim um sinal senoidal cuja freqüência dependeria dos valores do capacitor e do indutor.

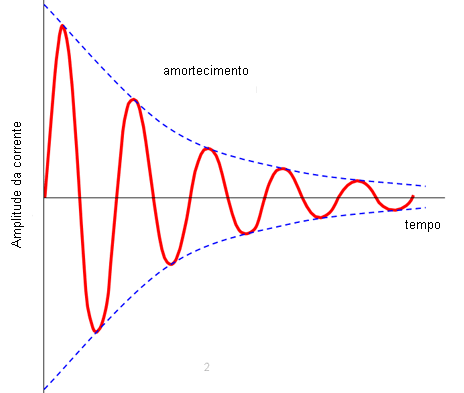
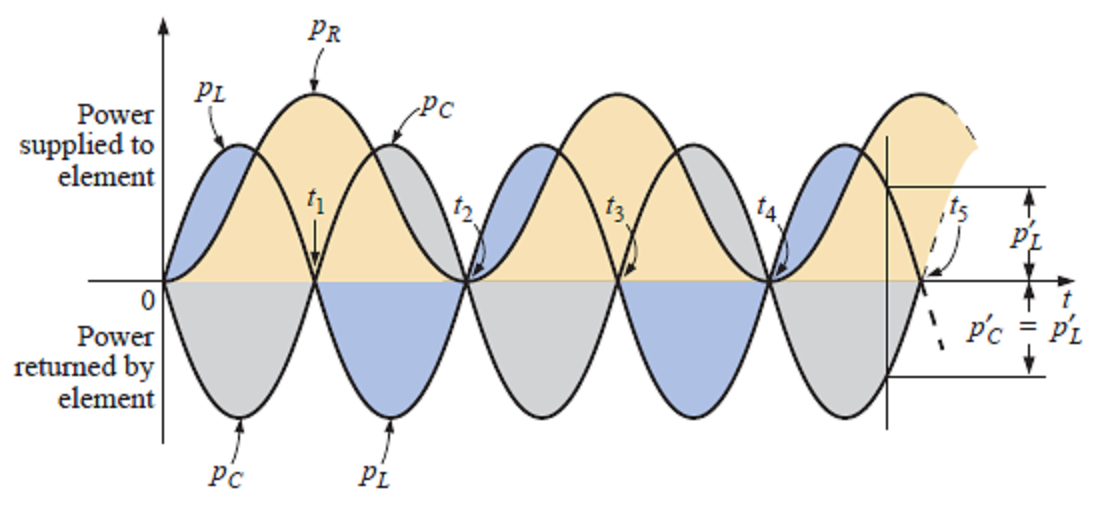
Na prática, entretanto, os condutores do indutor e do circuito representam uma resistência que absorve energia. Assim, a oscilação que ocorre é amortecida até desaparecer, conforme mostra a figura abaixo.

Se em cada ciclo produzido a energia perdida for reposta, teremos um sinal de amplitude constante.

Isso pode ser conseguido através de circuitos amplificadores, como ocorre nos denominados osciladores.

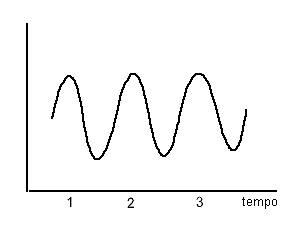
Num oscilador temos um componente (válvula ou transistor) que constantemente repõe a energia perdida em cada oscilação mantendo assim sua intensidade constante.

Na verdade, ele até repõe energia a mais, de modo que parte dela possa ser aproveitada num circuito externo, conforme mostra a figura:

Fator de qualidade

O fator de qualidade Q de um circuito ressonante em série é definido como a razão entre a potência reativa no indutor ou do capacitor e a potência média no resistor na frequência de ressonância:

Para o circuito RLC ressonante série:

Q = (ωs.L.I²)/(R.I²)

e

Q = (I²/ωs.C.)/(R.I²)

Portanto:

Impedância total em função da frequência

O módulo da impedância total é dado por:

R em função da frequência:

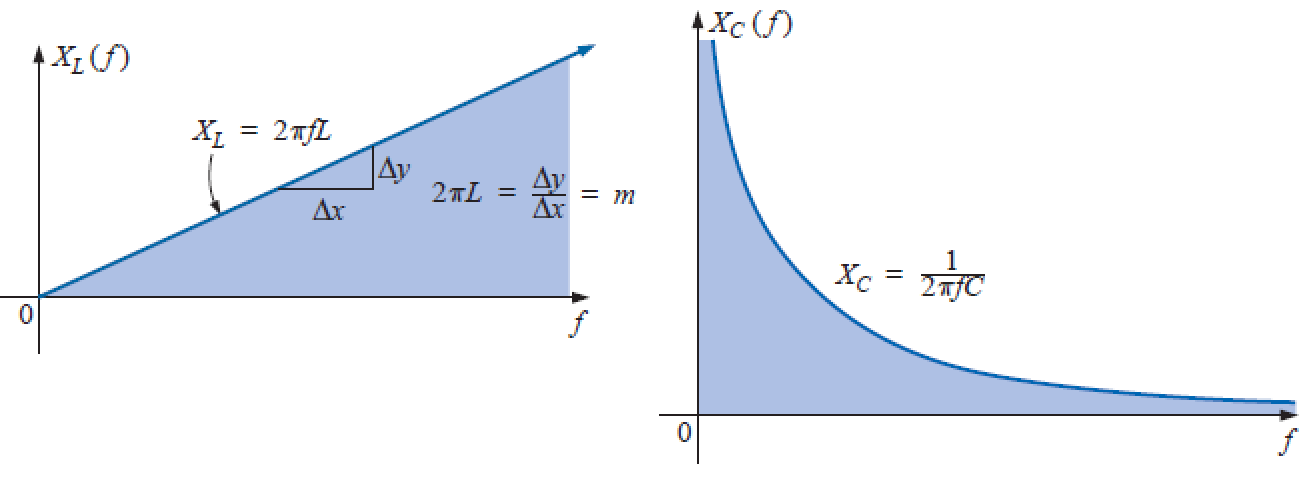
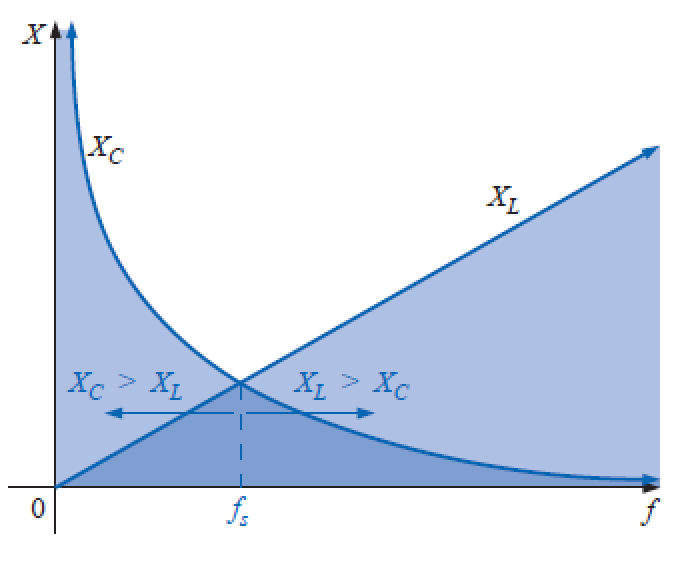
XL e XC em função da frequência:

Plotando L e C no mesmo gráfico:

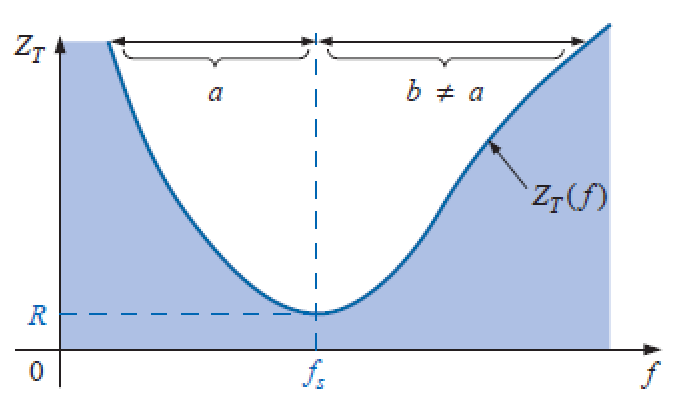
Impedância total em função da frequência para um circuito ressonante:

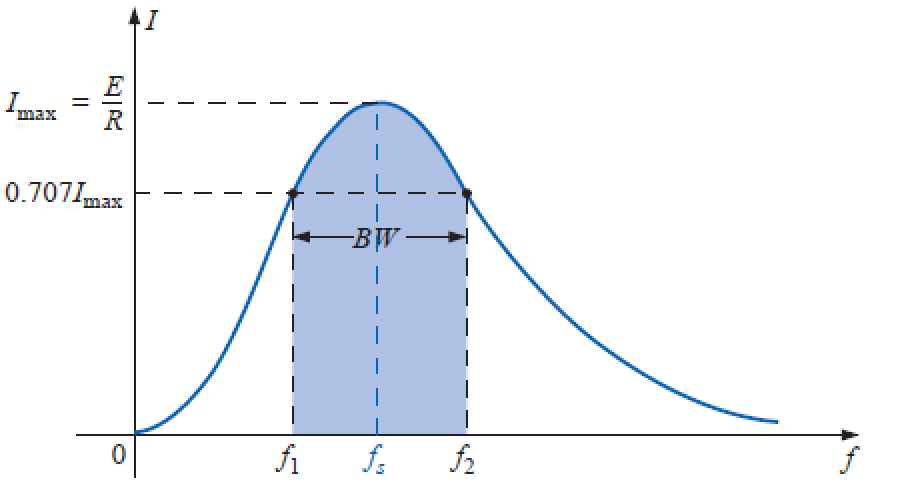
Se plotarmos a corrente em função da frequência para uma amplitude constante da tensão, obtemos:

Existe uma faixa de frequência na qual a corrente está próxima do valor máximo, e a impedância, do valor mínimo.

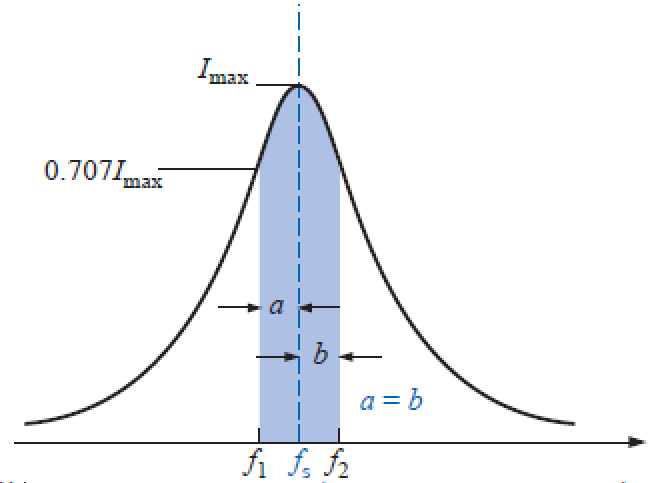
As frequências correspondem a 0,707 da corrente máxima e são denominadas:

• Frequência de banda
• Frequência de corte
• Frequências de meia potência ou frequências de canto (f1 e f2)

A faixa entre (f1 e f2) é conhecida como largura de banda (bandwidth –BW)

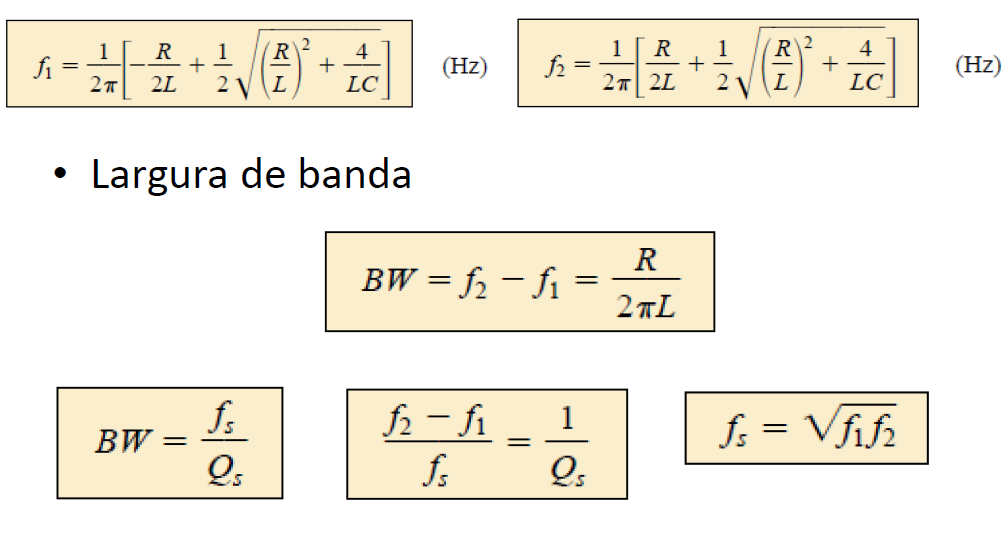
Frequências de meia potência são dadas por:

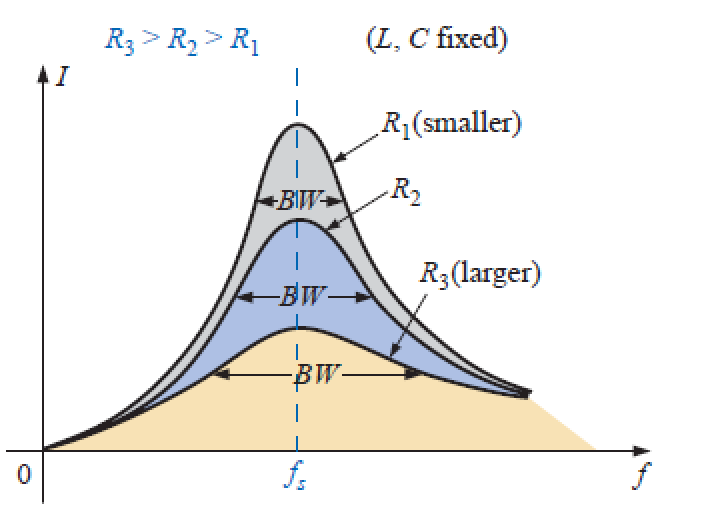
Curva de Seletividade em função de R

R variável:

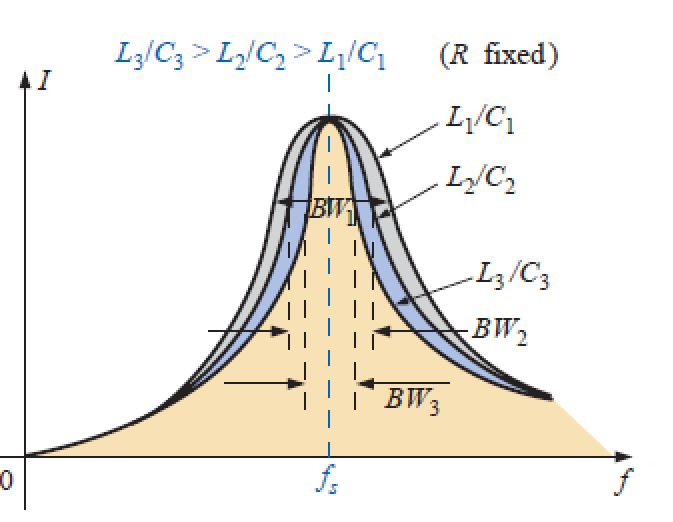
R fixo:

Curva aproximada paracircuito ressonante série para Q>10

Determinação de f1 e f2

Exemplo 1:

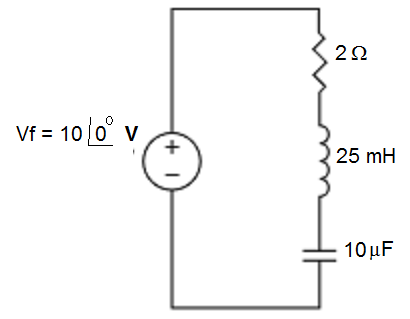
Considere o circuito mostrado abaixo. Determinar a frequência de ressonância, a tensão entre os terminais de cada elemento na condição de ressonância e o valor do fator de qualidade.

Solução:

A frequência de ressonância é obtida de:

ωs = 1/√(LC)
         
         = 1/√(0,025 x 0,0000010)

         = 2000 rad/s

A essa frequência, teremos:

I = V/Z = V/R = 5 ∠ 0°

Portanto:

Vr = 5 ∠ 0°.2 = 10 ∠ 0° V
Vl = j ωs L .5 ∠ 0° = 250 ∠ 90° V
Vc = 5 ∠ 0° . 1/j ωs C = 250 ∠ -90° V

Observe a magnitude das tensões entre os terminais do indutor e do capacitor, em relação à tensão de entrada!

Note também que são iguais, e defasadas de 180° uma da outra.

O fator de Qualidade é calculado como:

Q = (ωs.L)/R = 2000.0,025/2 = 25

Exemplo 2:

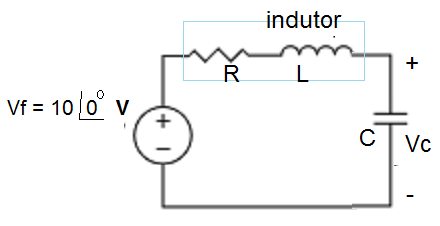
No laboratório de circuitos da universidade, os estudantes foram solicitados a construir um circuito RLC que entrasse em ressonância à frequência de f = 1000 Hz, a partir de um indutor de 0,02 H e com um fator de qualidade Q de 200. Um dos estudantes produziu o circuito mostrado abaixo, onde a resistência interna do indutor é representada por R. Se o capacitor escolhido para demonstrar a ressonância foi um capacitor constituído de papel impregnado de óleo, com limite de 300 V, determine os parâmetros do circuito e o efeito de escolha deste capacitor.

Solução:

Para que a ressonância ocorra a 1000 Hz, o estudante obteve o valor do capacitor necessário:

  ωs = 2πfs = 1/√(LC)

que vai fornecer C = 1,27 μF

O estudante selecionou um capacitor constituído de papel impregnado em óleo, com limite de 300V.

O valor do resistor foi obtido utilizando a expressão para Q, isto é:

Q = ωsL/R = 200

ou R = 1,59 Ω.

Na ressonância, a corrente seria:

  I = Vf/R

ou

 I= 6,28 ∠ 0° A

Quando construído, a corrente foi medida como sendo apenas

 I≅ 1 ∠ 0° mA
 

Isto mostrou claramente que a impedância vista pela fonte era de aproximadamente 10 kΩ de resistência, ao invés de 1,59 Ω.

Suspeitando que o capacitor fosse a fonte do problema, o estudante calculou a tensão que deveria ser associada ao capacitor.

Conforme previsto no projeto, seria:

  Vc = Vf/R . (1/jωC) = 2000 ∠ -90° V

que é uma tensão mais de 6 vezes maior do que a tensão limite do capacitor!!! Essa sobretensão danificou o capacitor, fazendo com que ele entrasse em curto e o circuito não funcionasse corretamente.

Com a substituição do capacitor e a fonte de tensão reduzida para 1∠ 0°, a rede apresentou funcionamento compatível com um circuito de alto Q.

Exercícios

1. Para o circuito ressonante a seguir, determine:

a) Vr, I, Vl e Vc

b) Fator de qualidade Q

c)Se a frequência de ressonância é de 5000Hz, determine a largura de banda

d)Qual a potência dissipada no circuito nas frequências de meia potência?

Solução

---

2. A largura de banda de um circuito ressonante em série é 400Hz:

a)Se a frequência de ressonância é 4000Hz, qual é o fator de qualidade Q?

b)Se R = 10Ω, qual é o valor de XL na ressonância?

c)Calcule a indutância L e a capacitância C do circuito.

d)Quais os valores comerciais prováveis de L e C?

Solução

---

3. Um circuito RLC série possui uma frequência de ressonância de 12.000 Hz

a)Se R=5 Ω e XL na ressonância é de 300 Ω, calcule a largura de banda

b)Calcule as frequências de corte

Solução

---

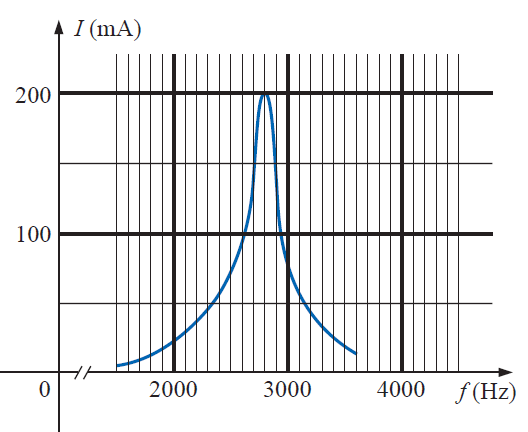
4.

a)Determine Qse a largura de banda para a curva de resposta na figura

b)Para C=100nF, determine R e L do circuito ressonante

c)Determine a tensão aplicada.

Solução

---

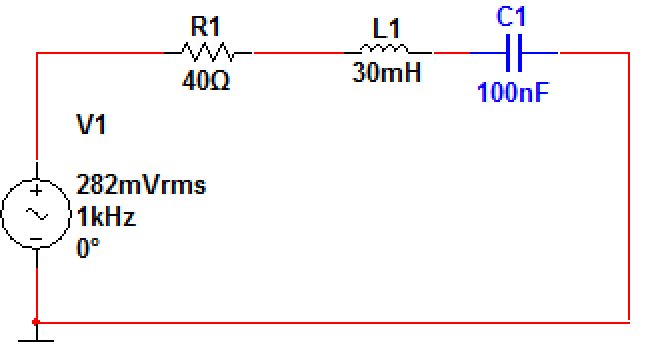
5. Para o circuito abaixo:

a) Calcule a frequência de ressonância

b) Simule o circuito a seguir no multisimou pspice.

c) Trace a curva de ressonância para a corrente.

d) O resultado em frequência foi próximo ao calculado?

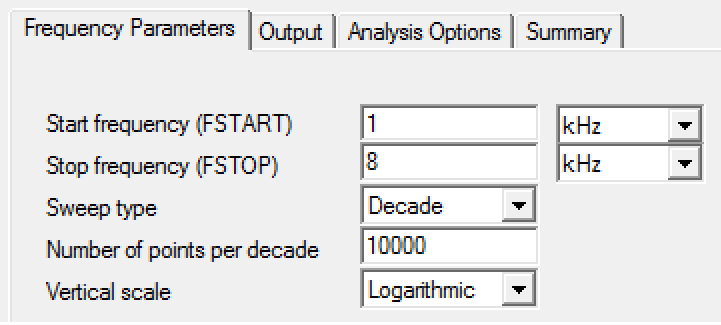
Dicas: No multisim, simular em Simulate->Analyses->AC Analysis... Configurar:

Potência em Circuitos Ressonantes

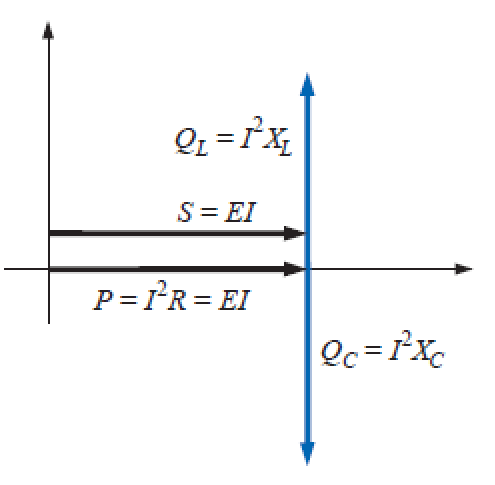
A potência média dissipada pelo resistor na ressonância é igual a I²R e as potências reativas no indutor e capacitor são I²XL e I²XC, respectivamente.

Temos o seguinte triângulo de potências:

logo:

  Fp = cos θ = P/S
  Fp = 1 !

Bibliografia

[1] SADIKU, M. N. O.; MUSA, S. M.; ALEXANDER, W. K. Análise de Circuitos Elétricos com Aplicações. Porto Alegre: Mc Graw Hill Education, 2014. v. 3.

[2] BOYLESTAD, R. L. Introdução à Análise de Circuitos. 12a ed. São Paulo: Pearson, 2011.

[3] PETRY, C. Circuitos 2. Disponível em: Aula 14 - Ressonância, 2023.

[4] BALDINI Fo., Renato. EA-513 Circuitos Elétricos, Notas de Aula, Disponível em: Circuitos Elétricos, 2014.

---

<< Página do curso

<< Fator de Potência	Ressonância	Transformadores >>