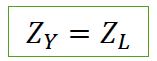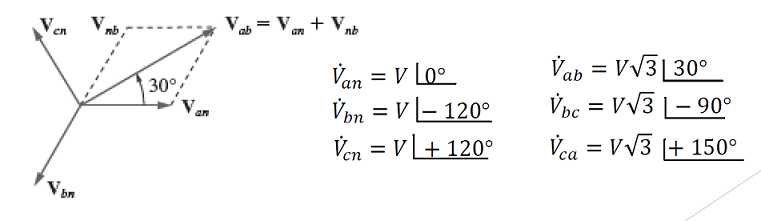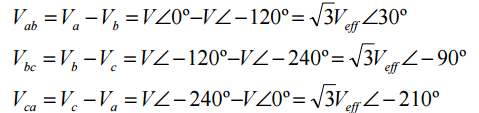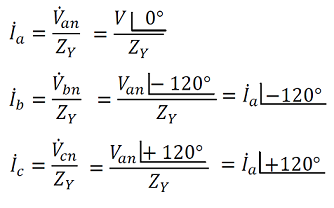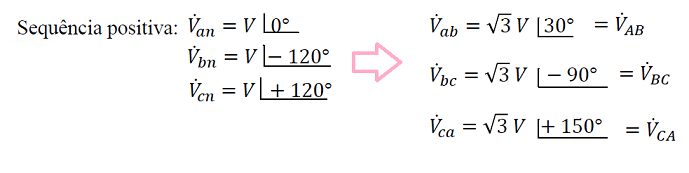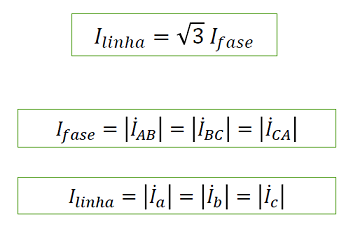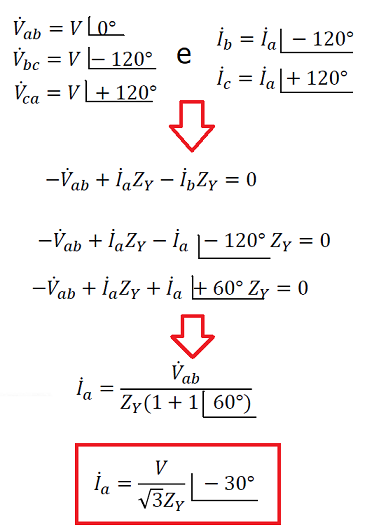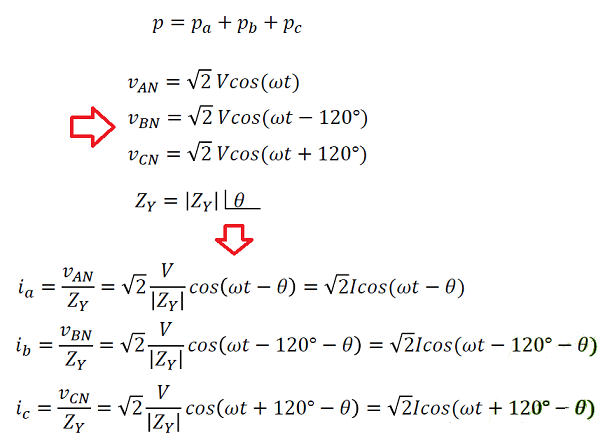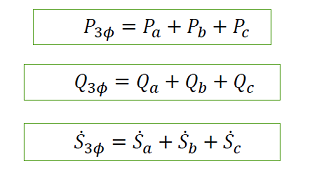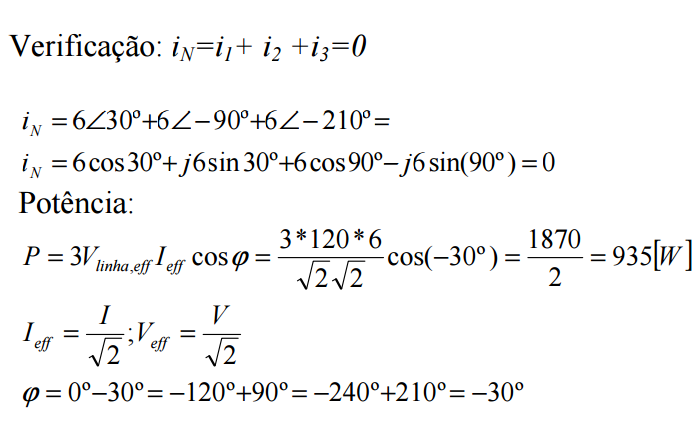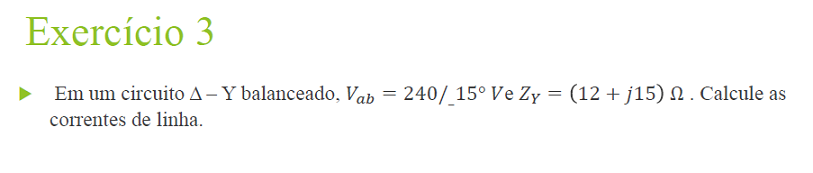AULA 14 - Circuitos Elétricos 2 - Graduação
Modificado de [1]
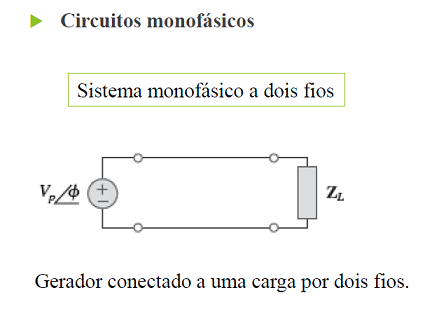
Circuitos Polifásicos
Circuitos polifásicos são circuitos nos quais as fontes CA operam na mesma frequência, mas com ângulos de fases diferentes.
A geração e transmissão de energia elétrica são mais eficientes em sistemas polifásicos que empregam combinações de 2, 3 ou mais tensões sinusoidais.
O sistema trifásico foi independentemente inventado por Galileo Ferraris, Mikhail Dolivo-Dobrovolski e Nikola Tesla, nos meados do fim da década de 1880.
Circuito Trifásico Balanceado
Ou "Circuito Trifásico Equilibrado".
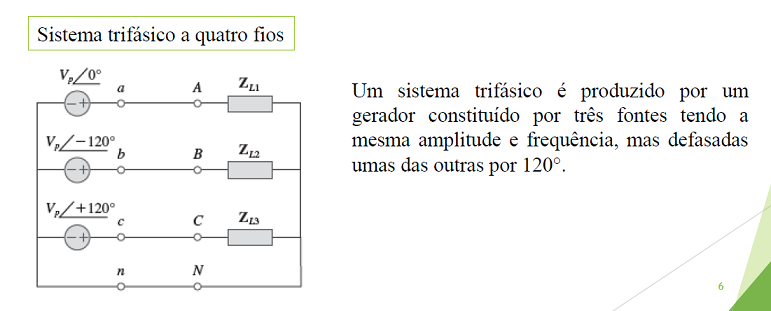
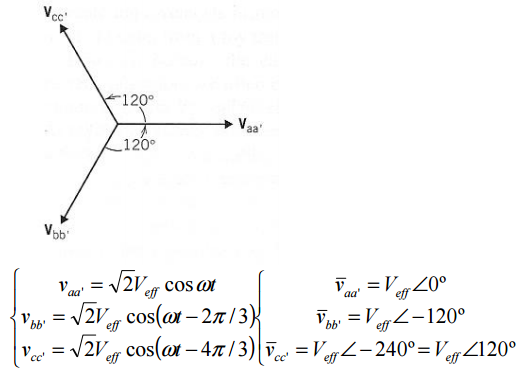
É constituído por 3 tensões sinusoidais possuindo amplitudes e frequências iguais, com desafamento de 120º entre si.
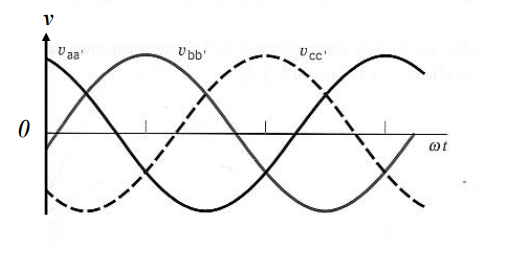
Vaa’ + Vbb’ + Vcc’ = 0
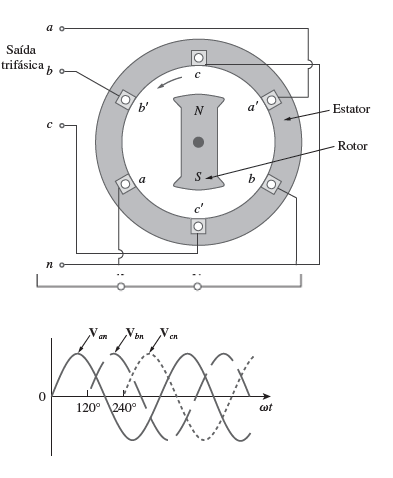
Isto é feito dispondo-se sobre o mesmo eixo, três bobinas deslocadas entre si de 2π/3 rad e girando o conjunto com velocidade angular constante no sentido horário, no interior de um campo magnético uniforme. Nos terminais das bobinas aparecerá um sistema de tensões de mesmo valor máximo e defasadas entre si de 2π/3 rad , conforme a Figura:
Gerador trifásico (alternador)
- Enrolamento estacionário → estator
- Ímã rotativo → rotor
- Bobinas com terminais a-a’, b-b’ e c-c’ estão fisicamente dispostas em 120º.
- À medida que o rotor gira, seu campomagnético “corta” as três bobinas e induz tensões nelas.
- Tensões induzidas nas três bobinas são iguais em magnitude, mas defasadas de 120º.
- Cada bobina pode ser considerada como um gerador monofásico, suprindo potência para cargas monofásicas ou trifásicas.
A Energia elétrica é,em geral, gerada e distribuída em sistemas trifásicos e frequências de 60Hz ou 50Hz.
A potência instantânea de um sistema trifásico pode ser constante (sem pulsos). Resultando em uma transmissão mais uniforme de potência e menos vibrações dos sistemas trifásicos.
Este sistema também é mais econômico que o sistema monofásico.
Sequência de fase
É o instante ou a ordem em que as tensões passam por um ponto fixo: seus valores máximos, por exemplo. Define-se, para um sistema polifásico simétrico, “seqüência de fase” como sendo a ordem pela qual as tensões das fases passam pelo seu valor máximo.
Por exemplo, no sistema trifásico das Figuras acima, a seqüência de fase é A-B-C, uma vez que as tensões passam consecutivamente pelo valor máximo na ordem A-B-C.
Evidentemente, uma alteração cíclica não altera a seqüência de fase, isto é, a seqüência A-B-C é a mesma que B-C-A e que C-A-B.
À seqüência A-B-C é dado o nome “seqüência direta” ou “seqüência positiva”, e à seqüência A-C-B, que coincide com C-B-A e B-A-C, dá-se o nome de “seqüência inversa” ou “seqüência negativa”.
Exemplo
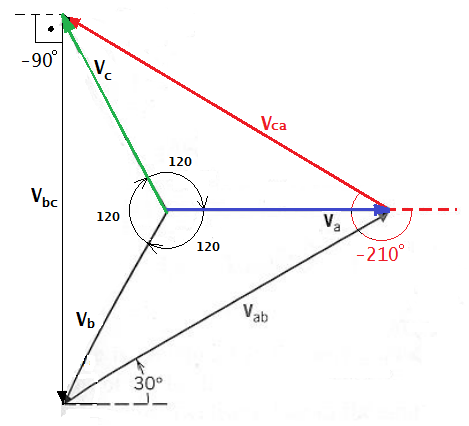
Um sistema trifásico simétrico tem seqüência de fase negativa, B-A-C, e VC = 220 ∠ 40° V . Determinar as tensões VA e VB .
Solução:
Sendo a seqüência de fase B-A-C, a primeira tensão a passar pelo valor máximo será VB , a qual será seguida, na ordem, por VA e VC . Portanto, deverá ser:
VB = Vm. cos( ωt + θ)
VA = Vm. cos( ωt + θ - 2π/3)
VC = Vm. cos( ωt + θ - 4π/3)
em que θ representa o ângulo inicial ou a rotação de fase em relação à origem.
No instante t=0, tem-se:
VB = Vm. cos(θ)
VA = Vm. cos(θ - 2π/3)
VC = Vm. cos(θ - 4π/3)
Sendo V = Vm/ √2 , fasorialmente tem-se:
VB = V ∠ θ
VA = V ∠ (θ - 2π/3)
VC = V. ∠(θ - 4π/3)
Por outro lado, sendo dado VC = 220 ∠ 40° V , resulta
V = 220 V
θ + 120 = 40° → θ = − 80°
e portanto
VB = 220 ∠ − 80°
VA = 220 ∠ − 200°
VC = 220. ∠ 40°
Tipos de conexão
Um típico sistema trifásico consiste em três fontes de tensão conectadas às cargas por três ou quatro fios (linhas de transmissão).
Um sistema trifásico é equivalente a três circuitos monofásicos.
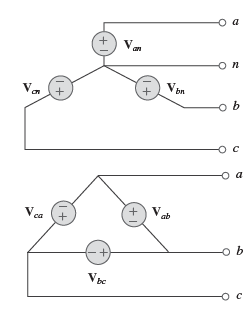
As formas em que as fontes de tensão estão conectadas podem ser estrela e delta:
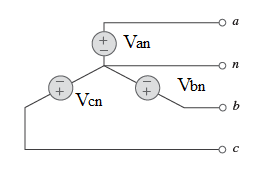
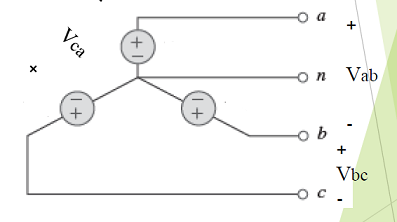
Tensões de fase
As tensões de fase são as tensões 𝑉𝑎𝑛, 𝑉𝑏𝑛 e 𝑉𝑐𝑛.
São as tensões entre as linhas a, b e c, respectivamente e o neutro n.
Tensões de linha
As tensões de linha são as tensões 𝑉𝑎𝑏, 𝑉𝑏𝑐 e 𝑉𝑐𝑎.
São as tensões entre as linhas a e b, b e c, e c e a, respectivamente.
Cargas balanceadas
Um sistema trifásico com cargas balanceadas significa que as Impedâncias são iguais em magnitude e fase.
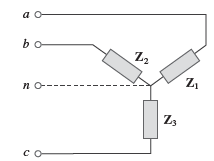
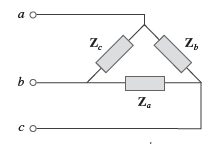
- Impedâncias de linha: 𝑍1, 𝑍2 e 𝑍3
- Impedâncias de fase: 𝑍𝑎, 𝑍𝑏 e 𝑍𝑐
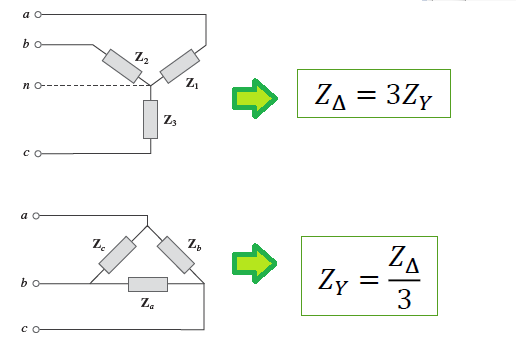
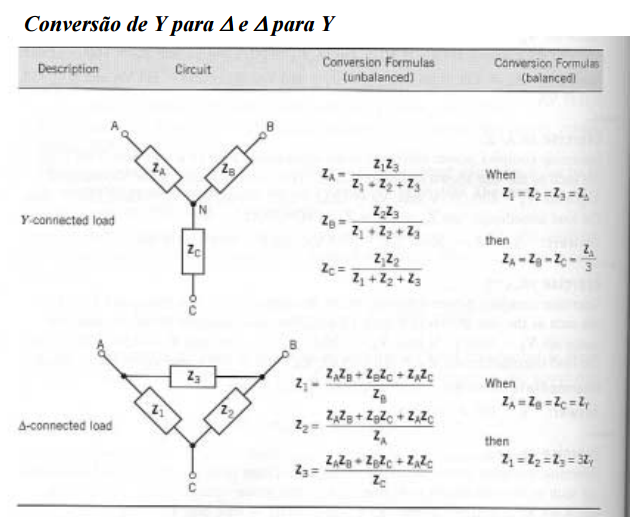
Cargas trifásicas - conversão
Quando as cargas são balanceadas:
𝑍1 = 𝑍2 = 𝑍3 = 𝑍𝑌 𝑍𝑎 = 𝑍𝑏 = 𝑍𝑐 = 𝑍Δ
onde
𝑍𝑌 → Impedância de carga por fase conectada em estrela 𝑍Δ → Impedância de carga por fase conectada em delta
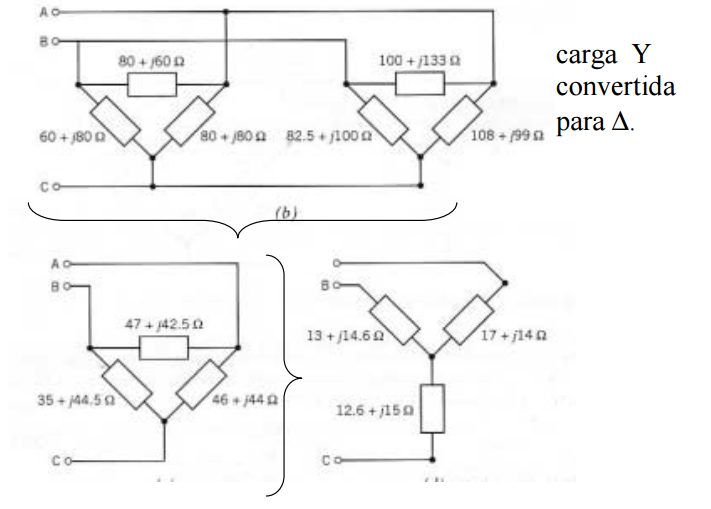
Exemplo:
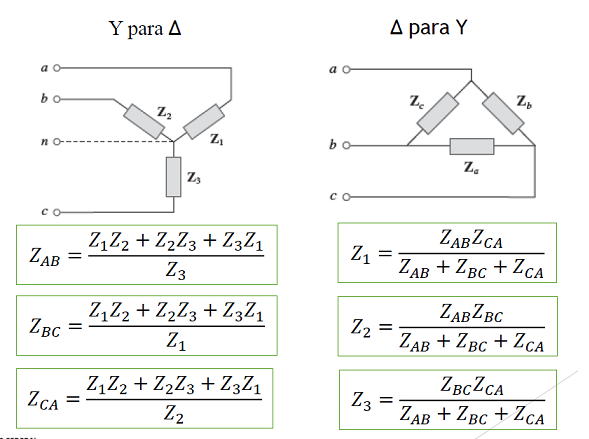
Converta as duas cargas Δ em paralelo, para carga Y, utilizando as relações de transformação:
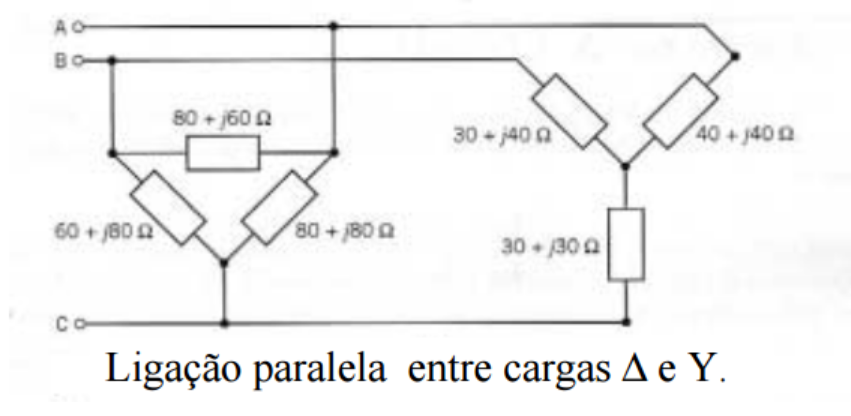
Exercício
Calcule qual a carga Δ correspondente à ligação de cargas abaixo:
Conexões fonte-carga de sistemas trifásicos balanceados
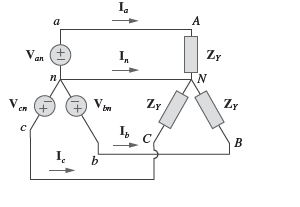
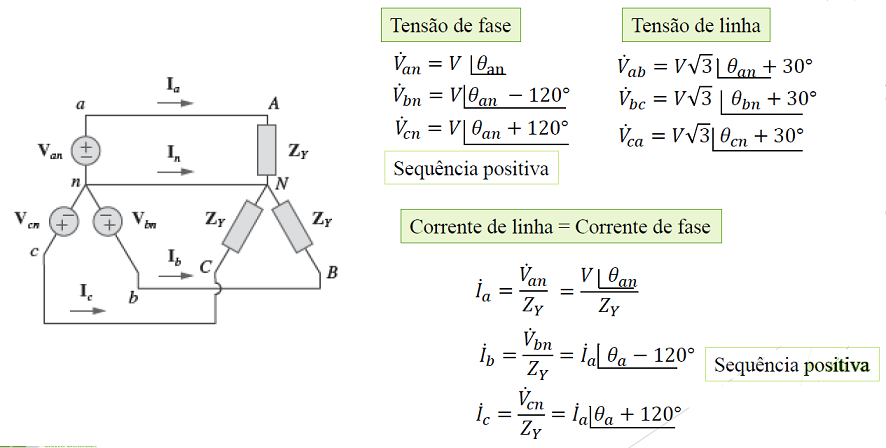
Conexão estrela-estrela balanceada (Y-Y)
Sistema trifásico com fonte balanceada conectada em Y e uma carga balanceada conectada também em Y.
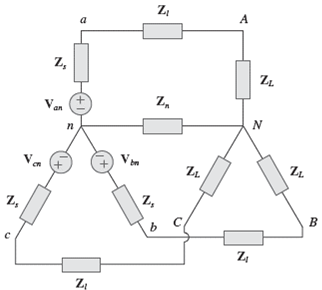
Considerando-se as impedâncias do circuito:
onde:
- 𝑍𝑠 - impedância da fonte
- 𝑍𝑙 - impedância da linha
- 𝑍𝑛 - impedância do condutor do neutro
- 𝑍𝐿 - impedância da carga
Assim:
𝑍𝑌 = 𝑍𝐿 + 𝑍𝑙 + 𝑍𝑠
Mas
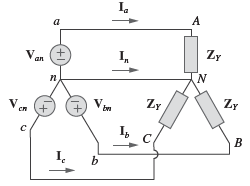
𝑍𝐿 ≫ 𝑍𝑠, 𝑍𝑙 e 𝑍𝑛
Então
As tensões serão:
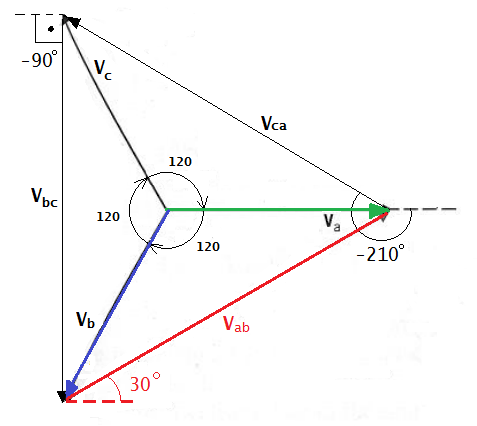
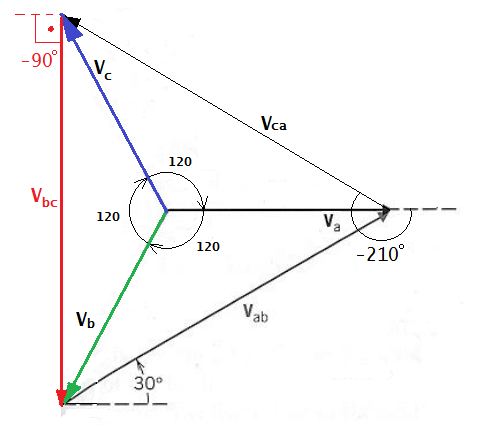
Tensões de linhas
As tensões de linha estão adiantadas das tensões de fase correspondentes em 30°.
Em outras palavras:
Já as correntes:
Então:
RESUMO
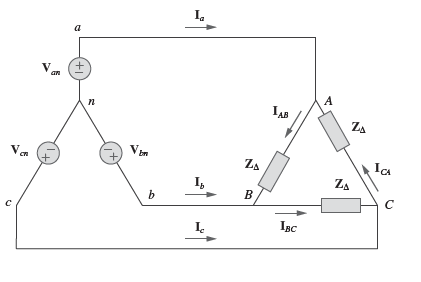
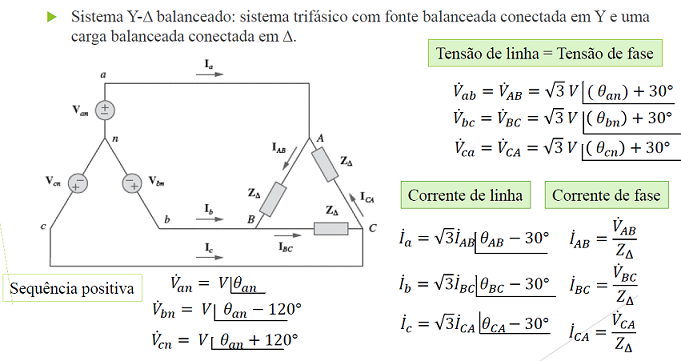
Conexão estrela-delta balanceada (Y-Δ)
Sistema trifásico com fonte balanceada conectada em Y e uma carga balanceada conectada em Δ.
Uma vez que a geração ainda é em Y, as tensões continuam sendo :
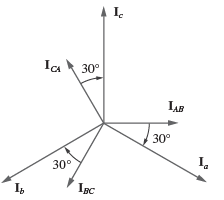
As correntes serão:
Ou seja, as correntes de linha estão 30° atrasadas em relação às correntes de fase, considerando a sequência positiva.
RESUMO
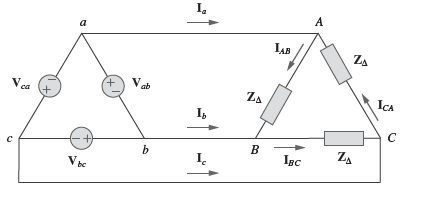
Conexão delta-delta balanceada (Δ-Δ)
Sistema trifásico com fonte balanceada conectada em Δ e uma carga balanceada também conectada em Δ.
As tensões serão:
As correntes serão:
RESUMO
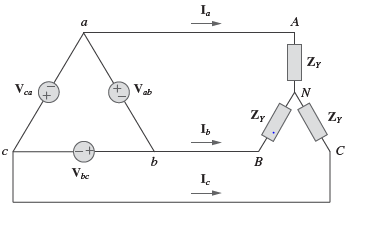
Conexão delta-estrela balanceada (Δ-Y)
Sistema trifásico com fonte balanceada conectada em Δ e uma carga balanceada conectada em Y.
Note que:
Portanto:
E
RESUMO
Potência em Circuitos Trifásicos balanceados
Potência instantânea absorvida pela carga P = V.I.
A potência total instantânea na carga é a soma das três potências instantâneas nas cargas.
Assumindo uma carga em Y.
Ou seja, a potência instantânea em um sistema trifásico balanceado é constante!
Não muda com o tempo como a potência em cada fase.
Válido para carga em Y ou em Δ.
Ou seja:
e
Circuitos Trifásicos desbalanceados
Nestes sistemas não será sempre verdade que as tensões de linha, as tensões de fase, as correntes de linha e as correntes de fase possuem mesmo módulo e são defasadas de 120°, como em sistemas balanceados.
Assim, torna-se necessário calcular TODAS as tensões e correntes individualmente, utilizando técnicas de análise de circuitos, como análise de malhas (LKT), análise de nós (LKC), lei de Ohm.
Potência em Circuito Trifásico desbalanceado
As potências em cada fase agora são diferentes, não pode-se multiplicar a potência de uma das fases por três para encontrar a trifásica.
Deve-se encontrar a potência em cada fase e somar às demais.
EXEMPLO:
Um sistema trifásico a 4 condutores, (tensão composta V∆ef = 208V) alimenta uma carga em estrela equilibrada, constituída por impedâncias 20∠−30º . Calcular as correntes da linha e a potência fornecida pelos geradores.
Bibliografia
[1] SADIKU, M. N. O.; MUSA, S. M.; ALEXANDER, W. K. Análise de Circuitos Elétricos com Aplicações. Porto Alegre: Mc GrawHillEducation, 2014. v. 3.
[2] BOYLESTAD, R. L. Introdução à Análise de Circuitos. 12aed. São Paulo: Pearson, 2011.
[3]GIF Gerador Síncrono
Exercícios
| << Transformadores | Circuitos Polifásicos |
|---|