AULA 2 - Eletrônica Digital 1 - Graduação

<<< Voltar para página principal do curso

Origem dos Sistemas de Numeração

Já nos tempos remotos, o ser humano sentia a necessidade de quantificar coisas, fossem cabeças de um rebanho, número de inimigos ou qualquer outra informação contável.

Todos os seres vivos possuem, de uma maneira ou de outra, a faculdade de comparar, seja ela qualitativa ou quantitativa, e são capazes de avaliar quantidades através de misteriosas sensações de suficiência e qualidades, mediante peculiares raízes instintivas de raciocínio.

No ser humano, particularmente, estas faculdades se desenvolveram de maneira acentuada.

Diante desta necessidade, o homem desenvolveu métodos requintados de quantificação.

Com o advento da socialização do ser humano, surgiram sistemas de contagem em planos abstratos, onde já não se dependia da presença física das coisas a serem quantificadas.

Provavelmente, o primeiro sistema a surgir foi o sistema unitário, o sistema baseado em um só dígito.

Provavelmente um antigo pastor de ovelhas Neanderthal recorria a desenhos para saber se nenhuma cabeça havia se extraviado. Utilizava como algarismos o desenho do quadrúpede e comparava a quantidade de desenhos com a quantidade de ovelhas.

Mais tarde passou a utilizar outro símbolo, pontos por exemplo, p/ designar uma ovelha.

Nascia aí, a partir da representação concreta, a representação abstrata e com estas, novos horizontes da matemática.

A partir disto, o homem atribuiu símbolos a quantidades maiores, como por exemplo,

.    = 1 (um ponto é igual a uma unidade);
..   = 2 (dois pontos igual à quantidade dois); 
...  = 3 (três pontos igual à quantidade três). 

Se o homem não tivesse feito isso, hoje escreveríamos o n° 5 como “.....” (cinco pontos) ou “11111”.

Os babilônios utilizavam grupos de luazinhas para representar grandezas de 0 a 9.

Os egípcios tinham um, dois e três sinais iguais p/ as grandezas 1, 2 e 3 e um sinal diferente para as grandezas de 4 a 9.

os romanos utilizavam sinais I, V, X, C, L, M.

Estes sistemas necessitavam de outros símbolos para quantidades ainda maiores (bilhões, trilhões, etc).

Presume-se que foram os indianos que primeiramente observaram que, adotando-se uma pequena coleção de símbolos ( 9 no caso), a posição de um símbolo em relação a outro bastaria para indicar grandezas maiores que o número de símbolos.

A idéia foi adotada e propagada pelos árabes, que denominaram símbolos de algarismos ( em homenagem ao famoso matemático Al-Khowârizmê).

Também foram os inventores do zero, símbolo indispensável ao sistema de numeração por ordens (também chamado de sistema de quantificação por notação posicional).

Curiosamente , os árabes não utilizaram sua própria invenção. Foram eles que inventaram os signos ou símbolos (desenhos que representam as quantidades de 0 a 9) que atualmente todo o mundo ocidental usa, enquanto eles, seus inventores, não o utilizam.

---

Nos sistemas de numeração que adotam o conceito de ordem, temos a primeira ordem representando as unidades com cada unidade representada por um símbolo diferente e em seguida, outras ordens (unitária, dezena, centena, decimal, centesimal etc).

Todos eles foram inventados baseados em 2 conveniências:

• a) haver poucos símbolos p/ memorização e
• b) possibilitar a representação de quantidades muito grandes.

Sistema decimal

A ordem das unidades contém 10 símbolos, 10 algarismos ( 0,1,2,3,4,5,6,7,8,9,), representando as dez grandezas peculiares a este sistema.

O número dez (10), formada por dois dos símbolos da ordem unitária, inaugura uma segunda ordem, a das dezenas; o 100 inaugura a 3°ordem, a das centenas e assim por diante.

Ainda uma especulação. Muito provavelmente foi o fato de termos 10 dedos nas mãos que influenciou a escolha de nossa espécie pelo sistema decimal, o que pode, sob certos aspectos, ser considerado como um fato infeliz, pois o sistema decimal não é, em absoluto, o melhor de todos. O sistema de base 12 seria muito mais vantajoso devido ao menor número de divisões quebradas que resulta.

[Vídeo-aula sobre Sistema Decimal]

Notação Posicional

<math>\cos x + \ln y +\operatorname{sgn}\, z</math>

A posição que um algarismo ocupa em relação aos demais e a base do sistema em questão nos fornece todos subsídios necessários para o entendimento e representação de uma grandeza ou quantidade. Todos os sistemas de numeração conhecidos têm uma notação definida, igual para várias bases, que torna possível a identificação de qualquer número baseado somente nos algarismos adotados pela base e nas posições que ocupam entre si.

Exemplo 2:

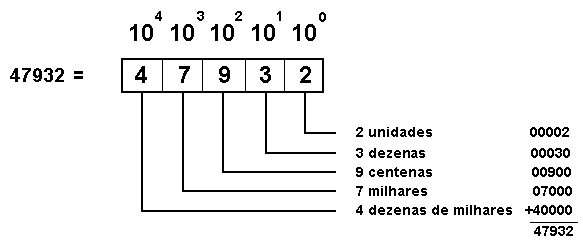
Outro exemplo: no número 1962 temos o algarismo um (1) na posição que indica milhares, o 9 na posição indicativa de centenas, o 6 na de dezenas e o 2 na posição de unidades.

Assim sabemos que o n°1962 é igual a:

1x1000 + 9x100 + 6x10 + 2x1 =  1000 + 900 + 60 + 2 = 1962.

Podemos escrever ainda, usando uma outra forma de representar a mesma coisa, que 1962 é igual a:

1x10³+ 9x10²+ 6x10¹+2x10° 

pois 1000 = 10³; 100 = 10²; 10 =10¹ e 1=10°.

O no 1962 está escrito na base dez, i.e., no sistema decimal.

Mas, a rigor, podemos generalizar para qualquer base:

Seja “b” a base de representação de um número e A, B, C, D, ... os símbolos dos algarismos deste sistema, então o número DCBA na base “b”, escrito convencionalmente como EDCBAb representa a grandeza:

D.b³ + C.b² + B.b¹+ A.b° .

Veja o exemplo.

123456= 1x10^5 + 2x10^4+ 3x10^3+ 4x10^2 + 5x10^1 + 6x10^0
= 100000 + 20000 + 3000 + 400 + 50 + 6

Onde, leia-se que x^y significa número x elevado à y-ésima potência".

0 mesmo “número”, numa base hipotética 5, representaria uma quantidade ou grandeza diferente:

= 1x5^5 + 2x5^4+ 3x5^3+ 4x5^2 + 5x5^1 + 6x5^0 
= 1x3125 + 2x625 + 3x125 + 4x25 + 5x5 + 6x1 
= 3125 + 1250 + 375 + 100 + 25 + 6
= 4.881 (diferente de 123.456)

Para representarmos a grandeza 123456 na base 5, precisaríamos do número 12422301, pois:

= 1 x 5^7 + 2 x 5^6 + 4 x 5^5 + 2 x 5^4 + 2 x 5^3 + 3 x 5^2 + 1 x 5^1 + 1 x 5^0 
= 1 x 78125 + 2 x 15625 + 4 x 3125 + 2 x 625 + 2 x 125 + 3 x 25 + 1 x 5 + 1 x 1
= 78125 + 31250 + 12500 + 1250 + 250 + 75 + 5 + 1
= 123456 d

O processo para a determinação deste número, isto é, a determinação de um número decimal em um número correspondente, em outra base, será tratado mais adiante.

Para entender mais: [[1] Sistema decimal de numeração - Wikipedia]

Sistema Binário

Os atuais computadores processam suas operações em um sistema diferente do decimal, o [sistema binário].

Enquanto no sistema DECimal temos 10 algarismos que representam valores, quais sejam:

• 0 – representando nada
• 1 – representando uma unidade de algo : .
• 2 – representando duas unidades de algo : . .
• 3 – representando três unidades de algo : . . .

...

• 9 – representando nove unidades de algo : . . . . . . . . .

o sistema BInário, como o nome já diz, só tem DOIS ALGARISMOS, apenas dois símbolos para representar quantidades.

Estes algarismos, os quais geralmente são representados pelos símbolos 0 e 1, correspondem a qualquer conjunto dual, como por exemplo:

• não e sim;
• falso e verdadeiro;
• desligado e ligado;
• negativo e positivo, etc.

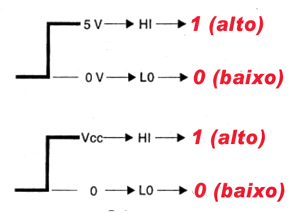
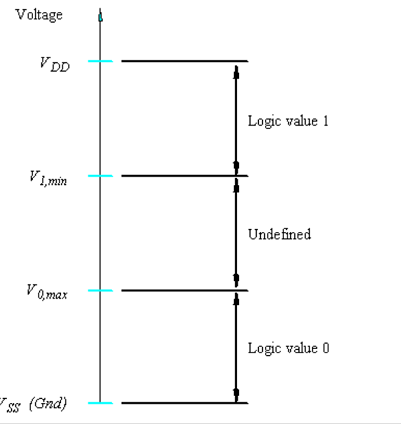
Nos circuitos lógicos, 0 e 1 representam, respectivamente, níveis de tensão baixo e alto ou estados de saturação e corte de transistores.

Cada dígito binário (em inglês, binary digit) é chamado de [bit].

Daí, uma outra designação comum: L e H ( Low e High levels, do inglês: baixo e alto níveis de tensão).

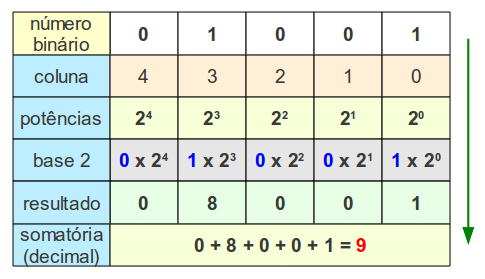
Exemplo:

Na base 2, o número decimal 11 (e grandeza ou quantidade 11 = 10 + 1) é representado pelo número binário 1011.

Diz-se que:

11d = 1011b

, onde d vem de sistema decimal e b, vem de sistema binário.

Vê-se que na base 2 foram necessários 4 algarismos binários para representar a grandeza 11, que no sistema decimal é representado por apenas dois sinais/algarismos.

Lembre-se também que o número na base 5 tinha muito mais algarismos que o mesmo número na base 10.

A explicação é simples.

Na primeira posição do sistema decimal (casa das unidades) podemos representar 10 grandezas (0 a 9), ao passo que na posição correspondente do sistema binário só podemos representar duas (0 e 1).

Cada casa decimal (que representa potências de 10) também equivale a mais de três casas binárias (que representa potências de 2).

Por estas razões, números em bases menores precisam de muito mais algarismos pra representar a mesma quantidade, que números em bases maiores.

Além disto, se acrescentarmos uma unidade à maior grandeza, da posição de casas decimais, a primeira ordem (ou posição) volta à grandeza menor e a próxima ordem é incrementada de uma unidade.

Exemplo:

19 + 1 = 20

Este é todo o segredo que envolve a passagem do no 9 p/ 1010.

O 9 volta para o zero (menor quantidade) e a posição das dezenas (anteriormente neste caso ocupada pelo algarismo zero, que não precisamos representar) é incrementada para 1, fornecendo o número 10.

Exemplos:

Descubra os próximos números para: a) 1234, na base 5; b) 1234, na base 6; c) 12, na base 3 ; d)12, na base 10 e e)19, na base 10

---

( Respostas: a)1240 b)1235 c)20 d)13 e)20, nas respectivas bases )

---

Valores representáveis

Como o sistema binário só tem dois algarismos, na 1° ordem podemos representar 2 valores:

0 e 1

Se utilizarmos a primeira e Segunda ordens, podemos representar até 4 grandezas:

00, 01, 10 e 11.

Com as 3 primeiras posições ou ordens, podemos representar até 8 grandezas:

000, 001, 010, 011, 100, 101, 110, 111

e assim por diante.

Note a relação:

2^(n° da ordem) = número de valores representáveis

Exemplo:

Com um número binário de 10 posições ou ordens podemos representar até:

2¹° = 1024 grandezas (da grandeza zero até a grandeza 1023)

, ao passo que dez posições no sistema decimal representariam:

10¹°= 10.000.000.000 ou dez bilhões de grandezas diferentes.

---

O sistema binário é usado em computadores devido à maior facilidade de se manipular eletronicamente somente duas grandezas, pela maior imunidade a [ruídos] e interferências.

No caso dos computadores e quaisquer outros dispositivos que utilizem circuitos eletrônicos digitais, precisamos ter somente “tensão presente” ou “tensão nula”, ou corte e saturação de transistores, para gerar os dois estados que correspondem aos bits 0 e 1.

Para saber mais: [Eletrônica Digital - Wikipédia em inglês]

Sistema Octal

Como já diz o nome, é o sistema de base 8 e, consequentemente, contém 8 algarismos (0,1,2,3,4,5,6 e 7).

É utilizado por ser um sistema que tem relação direta com o sistema binário.

Veremos esta relação quando tratarmos de transformação entre bases.

Neste sistema, a grandeza 8 é representada por 10, pois:

1x8¹ + 0x8°= 8+0

Para saber mais: [Sistema octal - Wikipédia em Inglês]

Sistema Hexadecimal

Do hexa=6 e deci=10, sistema numérico de base 16.

Tem 16 algarismos que são:

0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F.

A,B,C,D, E, e F fazem o papel das grandezas 10,11,12,13,14,15.

Usamos as letras maiúsculas pela necessidade de termos que representar cada uma destas grandezas com um único algarismo.

O sistema Hexadecimal é um sistema muito utilizado em computadores, pois permite uma leitura mais fácil, em comparação com os números binários.

Neste sistema, a grandeza 16 é representada por 10H, pois 1x16¹ + 0x16° = 16 + 1.

Ex: que grandeza representa o número 1AC H ?

Solução:

= 1 x 16² + A x 16¹ + C x 16°
= 1 x 16² + 10x 16¹ + 12x 16°

, uma vez que A e C representam 10 e 12 respectivamente

= 256 + 160 + 12 = 428 = 428d

Neste ponto, é conveniente perceber a diferença entre a grandeza 428 e a representação decimal da mesma, 428d.

A primeira representa uma quantidade de objetos ou coisas, enquanto a segunda é somente uma forma de representação daquela quantidade.

Um exemplo mais simples:

Temos três ovelhas num pasto.

A grandeza é 3 (que representa a quantidade de objetos-ovelha) é representada pelos números 3d, 11b 3o e 3h;

nos sistemas decimal, binário, octal e hexadecimal, respectivamente.

Para saber mais: [Sistema Hexadecimal - Wikipédia em Inglês]

RESUMO DE SISTEMAS NUMÉRICOS

Sistemas de numeração

Sistema	Base	Algoritmos	Maior representação na 1a. ordem
decimal	10	0,1,2,3,4,5,6,7,8,9	9
binário	2	0,1	1
octal	8	0,1,2,3,4,5,6,7	7
hexadecimal	16	0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F	15 ou F

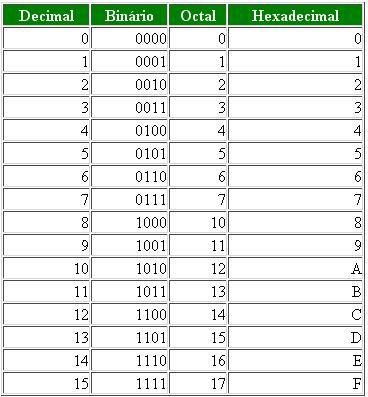
Tabela de conversão direta:

Conversão entre Bases: Decimal, binária, octal, hexadecimal:

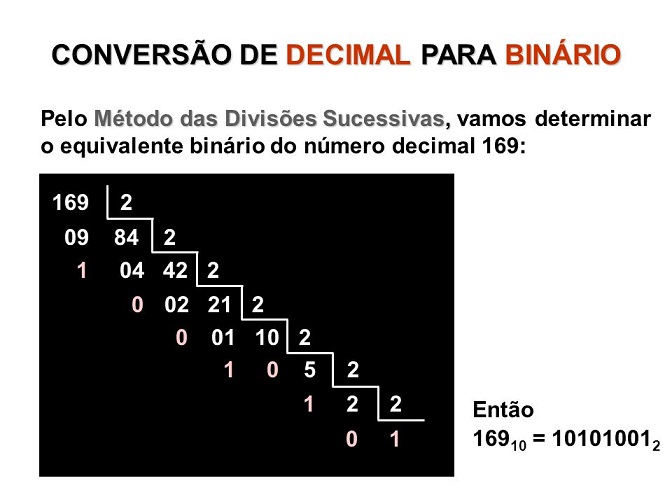
Conversão de Decimal → Binária

Técnica usual de transformação: Parte inteira

Para converter um número decimal inteiro em um número de base “b”, basta executar sua divisão aproximada por “b”, sucessivamente até que o enésimo dividendo não possa mais ser dividido por b, é ler os restos de trás para diante.

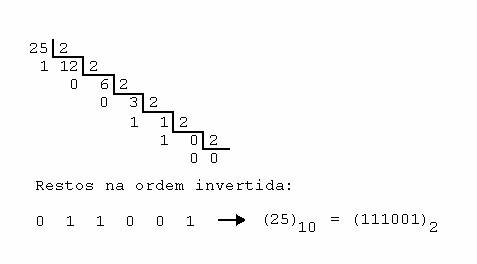
Veja o exemplo:

91d → Xb                                 

Onde q, b e r são inteiros e N é a parte inteira do número decimal

91 ∠ 2
   1 45 ∠2
      1  22 ∠2
           0 11 ∠2
                1 5 ∠2
                  1  2 ∠2
                     0  1 ∠2
                        1  0

Xb = 1011011b

No exemplo, o divisor é sempre a base para a qual se quer converter o número decimal; o último quociente inteiro passa a ser dividendo da próxima divisão. O processo continua até que o dividendo seja menor que o divisor ( a base), quando então passa a ser o último “resto”.

Outros exemplos

Parte Fracionária

O processo é diferente para a parte fracionária. Tomemos a seguinte exemplo:

91,6d → Xb

A parte inteira do número é convertida conforme o processo já demonstrado e obtemos o n° 1011011b.

A parte fracionária, 0,6 , é convertida da seguinte maneira:

Multiplica-se a parte fracionária (multiplicando) pela base “b” (multiplicador), neste caso o 2, e separa-se a parte inteira do produto. O resultado obtido da subtração da parte inteira do produto passa a ser o próximo multiplicando. Faz-se sucessivamente esta operação até que consiga uma precisão satisfatória. Lê-se os algarismos separados de cima para baixo. Veja o exemplo:

0,6 → Xb 0,6 → Xo (exercício)

0,6 x 2 = 1,2
menos a parte inteira (1) = 0,2
vezes 2  = 0,4
menos a parte inteira (0) = 0,4
vezes 2 = 0,8
menos a parte inteira (0) = 0,8
vezes 2 = 1,6
menos a parte inteira (1) = 0,6
vezes 2 = 1,2
menos a parte inteira (1) = 0,2  

e assim por diante

Lendo de cima para baixo teremos 10011, então 0,6d=10011b.

Se fizermos uma conferência, descobriremos que 0,10011b é igual a:

1 x 2^-1 + 0 x 2^-2 + 0 x 2^-3 + 1 x 2^-4 + 1 x 2^-5
= 1/2 + 1/16 + 1/32 
= 19/32 
= 0,59375

portanto, como podemos perceber, teremos sempre diferenças de precisão entre bases.

Outro exemplo:

Exercícios :

transforme os números decimais 0,5; 0,2; 0,25; 0,8 e 0,99 em números binários.

---

Binário, Octal, Hexadecimal → Decimal

Este processo serve para converter qualquer base para a base decimal.

O processo deriva da notação posicional comum a todos os sistemas de numeração que utilizam ordens. Tomemos como exemplo o número real:

 XYZ,WKb

onde X, Y ,Z, W e K são algarismos da base “b” e Z é o algarismo da 1a. ordem, Y da 2a. e X da terceira ordem da parte inteira.

W e K são algarismos das ordens fracionárias. Podemos dizer que cada um destes algarismos é multiplicado por um peso que depende da posição em que se encontra e da base em que esta expresso o número. Assim, os pesos dos sistemas numéricos ordenados serão sempre:

... b^4 b^3 b^2 b^1 b^0, b^-1 b^-2 b^-3 b^-4 …

e o no. genérico acima será:

X .b^2 + Y .b^1 + Z .b^0 + W .b^-1 + K .b^-2

com b^0= 1. Os exemplos práticos a seguir tornam isto mais claro.

Exemplo 1

 Pesos das posições   6  5  4  3  2  1  0  -1  -2  -3  -4  -5
                      1  0  1  1  0  1  1,  1   0   0   1   1b    →  Xd

1x2^6 +0x2^5 +1x2^4 +1x2^3 +0x2^2 +1x2^1 +1x2^0 +1x2^-1 +0x2^-2 +0x2^-3 +1x2^-4 +1x2^-5 =
 64 + 0 + 16 + 8 + 0 + 2 + 1 + 1/2 + 0 + 0 + 1/16 + 1/32 
 = 91,59375 ou  → 91,610

Exemplo 2

13A,Ch →  Xd

na base 16, A=10 e C=12, então:

1x16^2 + 3x16^1 + 10x16^0 + 12x16^-1 
= 256 + 48 + 10 + 12/16 
=314,7510

Exemplo 3

 265,418  →  Xd
=  2x8^2 + 6x8^1 + 5x8^0 + 4x8^-1 + 1x8^-2
= 128 + 48 + 5 + 4/8 + 1/64 

→ 181,5156310

Conversão entre bases binária, octal e hexadecimal

Sendo 2, 8 e 16 potências de 2, as conversões entre os sistemas binário, octal e hexadecimal são imediatas, como se poderá ver.

Binário → octal

8=2³

separa-se o número binário em grupos de 3 algarismos, e transforma cada grupo diretamente p/ a base 8

Ex: 10110101b para a base oito

10 110 101b

10b = 2o;  110b=6o; 101b= 5o; 
→ 265o

Para aprender mais: [Vídeo-aula sobre conversão Binário → Octal]

Binário → Hexadecimal

16=2^4

separa-se o número binário em grupos de 4 algarismos e transforma-os diretamente p/ a base 16

Ex: 1011.0101b

1011 0101b

1011b = 11d = Bh;  0101b = 5h
→ B5h

Para saber mais: [Vídeo-aula sobre Conversão de binário para Hexadecimal]

Octal → binário

Cada algarismo octal gera a mesma grandeza em um grupo de 3 algarismos binários

724h → Xb

7 = 111b
2 = 010b
4 = 100b

→ 111010100b

Hexa → binário

Cada algarismo hexadecimal gera a mesma grandeza em um grupo de 4 algarismos binários

BF1h → Xb

B = 11d = 1011b
F = 15d = 1111b
1 = 01d = 0001b

→ 1011.1111.0001b

A conversão de um número X na base genérica b1 para um em outra base b2 é efetuada através da conversão do primeiro número Xb1 para a base 10 e da base 10 para a base b2.

Exercícios propostos

1. 1990d → Xb
2. 10101010b → Xd, Xo, Xh
3. AB2,Ch → Xd, Xb
4. 40,2510 → Xh
5. 54o → X9
6. F8h → X4
7. 110111b + 72o → Xd
8. F8h - 26o → Xd
9. 20três+ 40cinco → Xd
10. 27d - 110b → Xh
11. 100b x 14h → Xd

Definições

Antes de passarmos aos códigos, é necessário conceituarmos alguns vocábulos doravante utilizados.

bit (pron. bit) → O vocábulo surgiu da contração abreviada de “binary digit” do inglês e representa os valores possíveis que uma variável lógica ( binária) pode assumir, 0 e 1

byte (pron. ba’it) → grupo ou palavra de 8 bits (ex: 010111010)

nybble (pron. ni’bôu) → grupo ou palavra de 4 bits (ex: 0111)

word: palavra (pron. uô.rd) → Palavra é qualquer conjunto de bits que contém ou representa um item de informação

Ex: Se 01 faz com que um sistema gire um motor em um sentido, 10 gira-o noutro sentido e 00 desliga o motor, então 01,10 e 00 são palavras porque carregam em si uma “informação”.

<<	AULA 2 - Sistemas de Numeração	>>