AULA 17 - Eletrônica Digital 1 - Graduação
<<< Voltar para página principal do curso
Circuitos Sequenciais
Os circuitos lógicos combinacionais permitem funções como decodificação, soma e subtração, comparação e muitas outras. Por definição, os circuitos combinacionais apresentam saídas que dependem, única e exclusivamente, das entradas atuais do circuito.
Entretanto, funções mais avançadas (que dependem do tempo, memorização de dados, sequência de operações etc.) não podem ser implementadas com o mesmo princípio. Nesse caso, devemos recorrer ao projeto de circuitos lógicos sequenciais.
Em um circuito sequencial, os valores das saídas em determinado instante dependem não só da combinação das variáveis de entrada, mas também do valor anterior, isto é, do valor que a saída tinha antes da aplicação da nova combinação de valores nas entradas. Além disto, estes circuitos normalmente dependem de um sinal pulsado, operam sob o comando de uma sequência de pulsos denominada de clock.
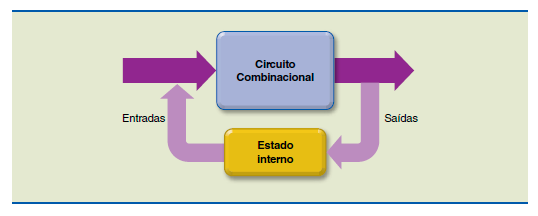
Na Eletrônica digital sequencial, utiliza-se dispositivos de memória elementares capazes de armazenar as variáveis de saída internamente a cada transição de estado (figura).
Um dos dispositivos mais elementares de memória, em Eletrônica Digital é o Flip-Flop.
O Flip-Flop (FF), ou multivibrador biestável, ou ainda latch, é capaz de armazenar um bit, dependendo do valor da sua entrada atual e de entradas passadas.
De modo geral, representa-se um FF como um circuito de duas saídas, Q e Q', entradas das variáveis e a entrada de controle clock.
Existem diversos tipos de flip-flops. De modo geral, são eles:
Flip-Flop SR
Também chamado de SC ("set-and-clear").
O FF básico SR ("set-and-reset") é o elemento de Eletrônica Digital Sequencial mais simples que existe. Todos os outros são derivados dele.
SR com portas NOR
O circuito do FF SR, implementado a partir de portas NOR, nada mais é do que duas portas NOR conectadas por realimentações cruzadas:
isto é:
Qi = (R + Q'i-1)'
Q'i = (S + Qi-1)'
Note, então, que as conexões de realimentação fazem com que as saídas atuais Qi e Q'i dependam das entradas S e R, mas também (já que também são entradas das portas NOR internas) das saídas anteriores Qi-1 (e Q'i-1, que é a saída Qi-1 barrada).
Análise do ff SR com portas NOR
Vamos analisar a tabela-verdade para as entradas S, R e clock, tendo em vista as saídas atuais Q e Q', além das saídas dos ciclos anteriores de relógio, lembrando que a porta NOR apenas fornece saída 1 quando todas as entradas forem 0.
| # | S | Qi-1 | R | Q'i-1 | Qi | Q'i |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | X | X |
| 2 | 0 | 0 | 0 | 1 | 0 | 1 |
| 3 | 0 | 0 | 1 | 0 | X | X |
| 4 | 0 | 0 | 1 | 1 | 0 | 1 |
| 5 | 0 | 1 | 0 | 0 | 1 | 0 |
| 6 | 0 | 1 | 0 | 1 | X | X |
| 7 | 0 | 1 | 1 | 0 | 0 | 0 (-> 1) |
| 8 | 0 | 1 | 1 | 1 | X | X |
| 9 | 1 | 0 | 0 | 0 | X | X |
| 10 | 1 | 0 | 0 | 1 | 0 (-> 1) | 0 |
| 11 | 1 | 0 | 1 | 0 | X | X |
| 12 | 1 | 0 | 1 | 1 | 0 | 0 |
| 13 | 1 | 1 | 0 | 0 | 1 | 0 |
| 14 | 1 | 1 | 0 | 1 | X | X |
| 15 | 1 | 1 | 1 | 0 | 0 | 0 |
| 16 | 1 | 1 | 1 | 1 | X | X |
Note que as entradas Q e Q' são complementares, por definição. Assim, os estados das linhas 1, 3, 6, 8, 9, 11, 14 e 16, que preveem Q=Q' são irrelevantes/inexistentes.
A partir disto, a TV já pode ser resumida por:
| # | S | Qi-1 | R | Q'i-1 | Qi | Q'i |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 2 | 0 | 0 | 1 | 1 | 0 | 1 |
| 3 | 0 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 1 | 1 | 0 | 0 | 0 (-> 1) |
| 5 | 1 | 0 | 0 | 1 | 0 (-> 1) | 0 |
| 6 | 1 | 0 | 1 | 1 | 0 | 0 |
| 7 | 1 | 1 | 0 | 0 | 1 | 0 |
| 8 | 1 | 1 | 1 | 0 | 0 | 0 |
S=R=1
Agora, note pelas linhas 6 e 8, que, quando as entradas S e R são iguais a 1, o FF SR vai para um estado incoerente, indesejável, com Qi=Q'i=0!
Como as saídas, por definição, devem ser complementares, este estado (S=R=1) é chamado de entrada não-permitida, ou restrita.
Esta condição reduz a TV a:
| # | S | Qi-1 | R | Q'i-1 | Qi | Q'i |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 2 | 0 | 0 | 1 | 1 | 0 | 1 |
| 3 | 0 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 1 | 1 | 0 | 0 | 0 (-> 1) |
| 5 | 1 | 0 | 0 | 1 | 0 (-> 1) | 0 |
| 6 | 1 | 0 | 1 | 1 | não-permitido | |
| 7 | 1 | 1 | 0 | 0 | 1 | 0 |
| 8 | 1 | 1 | 1 | 0 | não-permitido |
S=R=0
Agora, pelas linhas 1 e 3, fica mais fácil perceber que, sempre que S=0 e R=0, a saída Q/Q' irá se manter a mesma.
Se Q anterior era 0 (e, portanto, Q'i-1 era 1), a saída 0/1 será mantida. Ao contrário, se Qi-1/Q'i-1 era 1/0, esta será a saída futura Qi/Q'i do FF.
Assim, a TV fica:
| # | S | Qi-1 | R | Q'i-1 | Qi | Q'i |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 1 | Qi-1 | Q'i-1 |
| 2 | 0 | 0 | 1 | 1 | 0 | 1 |
| 3 | 0 | 1 | 0 | 0 | Qi-1 | Q'i-1 |
| 4 | 0 | 1 | 1 | 0 | 0 | 0 (-> 1) |
| 5 | 1 | 0 | 0 | 1 | 0 (-> 1) | 0 |
| 6 | 1 | 0 | 1 | 1 | não-permitido | |
| 7 | 1 | 1 | 0 | 0 | 1 | 0 |
| 8 | 1 | 1 | 1 | 0 | não-permitido |
As duas últimas condições da tabela exigem um pouco mais de atenção.
S=0 e R=1
Para estas entradas, descritas nas linhas 2 e 4, o FF SR funciona no modo Reset (R), isto é, zerando a saída Qi (e setando a Q'i, obviamente).
Na condição em que Qi-1 = 0 (e Q'i-1 = 1), da linha 2, é fácil constatar-se que:
- Qi = (R + Q'i-1)' = (1 + 1)' = (1)' = 0 e
- Q'i = (S + Qi-1) = (0 + 0)' = (0)' = 1
confirmando que o FF será resetado, isto é, zerado.
Porém, a condição Qi-1 = 1 e Q'i-1 = 0 exige um pouco mais de reflexão, porque, inicialmente, leva a:
- Qi = (R + Q'i-1)' = (1 + 0)' = (1)' = 0 e
- Q'i = (S + Qi-1) = (0 + 1)' = (1)' = 0 !!!!
que seria uma saída proibida, indesejável, já que Qi=Q'i. Ocorre, porém, que este estado de saída indesejável é temporário!
Logo, com a mudança de Qi para 0, a saída Q'i vai tender a:
- Q'i = (S + Qi-1) = (0 + 0)' = (0)' = 1
confirmando o Reset.
Assim, a TV ficaria:
| # | S | Qi-1 | R | Q'i-1 | Qi | Q'i |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 1 | Qi-1 | Q'i-1 |
| 2 | 0 | 0 | 1 | 1 | 0 (RESET) | 1 |
| 3 | 0 | 1 | 0 | 0 | Qi-1 | Q'i-1 |
| 4 | 0 | 1 | 1 | 0 | 0 (RESET) | 1 |
| 5 | 1 | 0 | 0 | 1 | 0 (-> 1) | 0 |
| 6 | 1 | 0 | 1 | 1 | não-permitido | |
| 7 | 1 | 1 | 0 | 0 | 1 | 0 |
| 8 | 1 | 1 | 1 | 0 | não-permitido |
S=1 e R=0
Para estas entradas, descritas nas linhas 5 e 7, o FF SR funciona no modo Set (S), isto é, levando a saída Qi a 1 (e zerando/resetando a Q'i, obviamente).
Na condição em que Qi-1 = 1 (e Q'i-1 = 0), da linha 7, é fácil constatar-se que:
- Qi = (R + Q'i-1)' = (0 + 0)' = (0)' = 1 e
- Q'i = (S + Qi-1) = (1 + 1)' = (1)' = 0
confirmando que o FF será setado, isto é, levado ao nível lógico 1.
Porém, a condição Qi-1 = 1 e Q'i-1 = 0, da linha 5, exige um pouco mais de reflexão, porque, inicialmente, leva a:
- Qi = (R + Q'i-1)' = (0 + 1)' = (1)' = 0 e
- Q'i = (S + Qi-1) = (1 + 0)' = (1)' = 0 !!!!
que também seria uma saída proibida, indesejável, já que Qi=Q'i. Mas este estado de saída indesejável também é temporário!
Logo, com a mudança de Qi' para 0, a saída Qi vai tender a:
- Qi = (R + Q'i-1) = (0 + 0)' = (0)' = 1
confirmando o Set.
Assim, a TV ficaria:
| # | S | Qi-1 | R | Q'i-1 | Qi | Q'i |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 1 | Qi-1 | Q'i-1 |
| 2 | 0 | 0 | 1 | 1 | 0 (RESET) | 1 |
| 3 | 0 | 1 | 0 | 0 | Qi-1 | Q'i-1 |
| 4 | 0 | 1 | 1 | 0 | 0 (RESET) | 1 |
| 5 | 1 | 0 | 0 | 1 | 1 (SET) | 0 |
| 6 | 1 | 0 | 1 | 1 | não-permitido | |
| 7 | 1 | 1 | 0 | 0 | 1 (SET) | 0 |
| 8 | 1 | 1 | 1 | 0 | não-permitido |
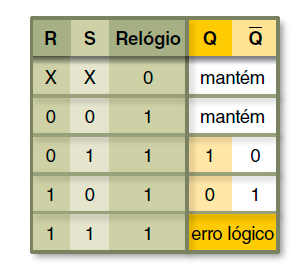
Após toda esta explanação detalhada, fica fácil entender porque a TV do FF SR (implementado com portas NOR) é descrita resumidamente por:
| S | R | Qi |
|---|---|---|
| 0 | 0 | Qi-1 |
| 0 | 1 | 0 (RESET) |
| 1 | 0 | 1 (SET) |
| 1 | 1 | não-permitido |
Ou seja, este FF, que é chamado de ASSÍNCRONO tem seu funcionamento resumido por:
- quando S=R=0, a saída do FF atual mantém as saídas anteriores;
- quando S = 0 e R = 1, o FF está na função reset, isto é, zerando a saída Qi (e setando Q'i);
- quando S = 1 e R = 0, o FF está na função set, isto é, setando a saída Qi (e zerando Q'i);
- a entrada S=R=1 é uma condição inaceitável, que leva à instabilidade do FF.
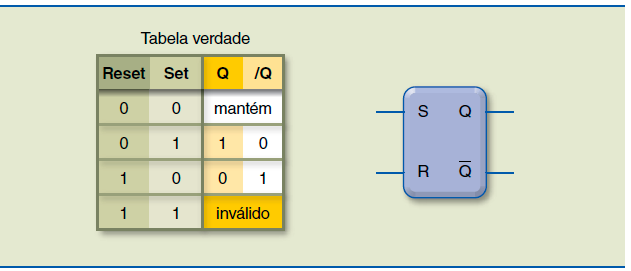
A simbologia do SR é dada por:
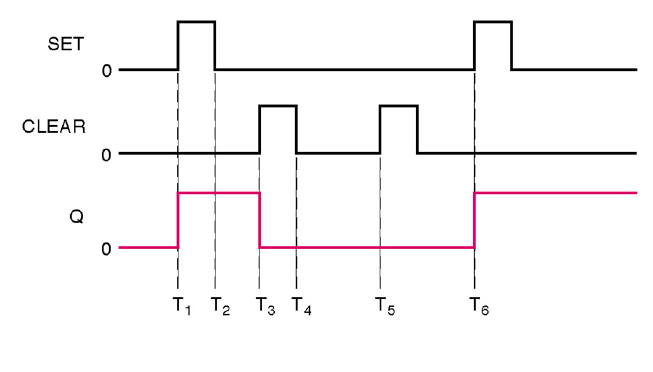
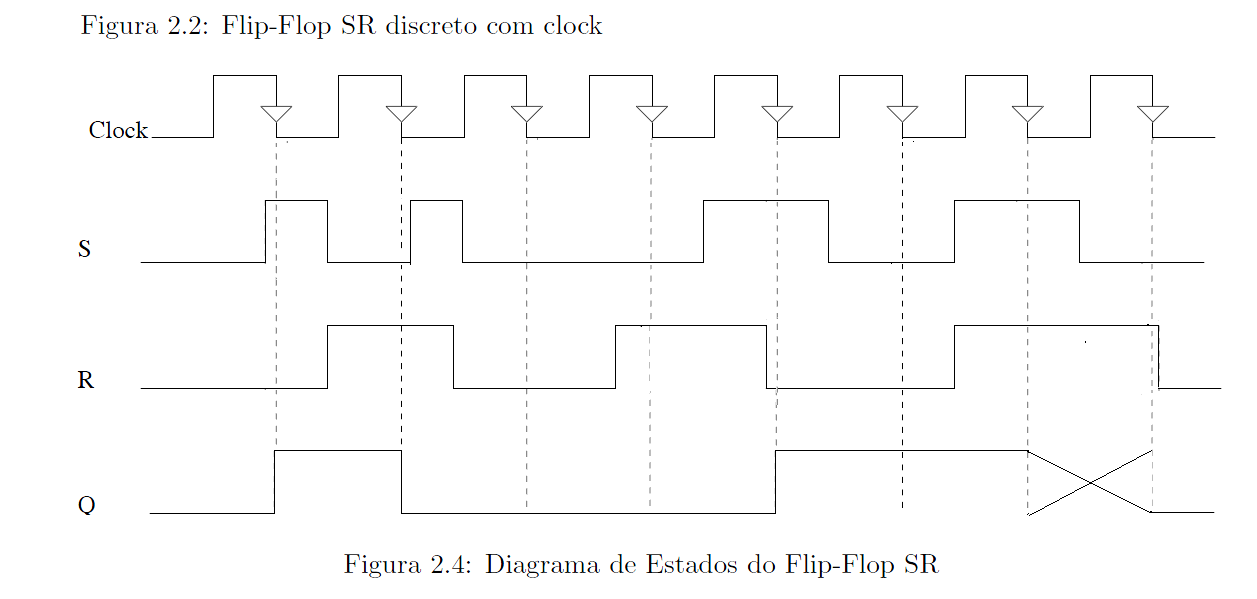
E, no tempo, o comportamento do SR Assíncrono pode ser descrito como abaixo:
Exercícios propostos
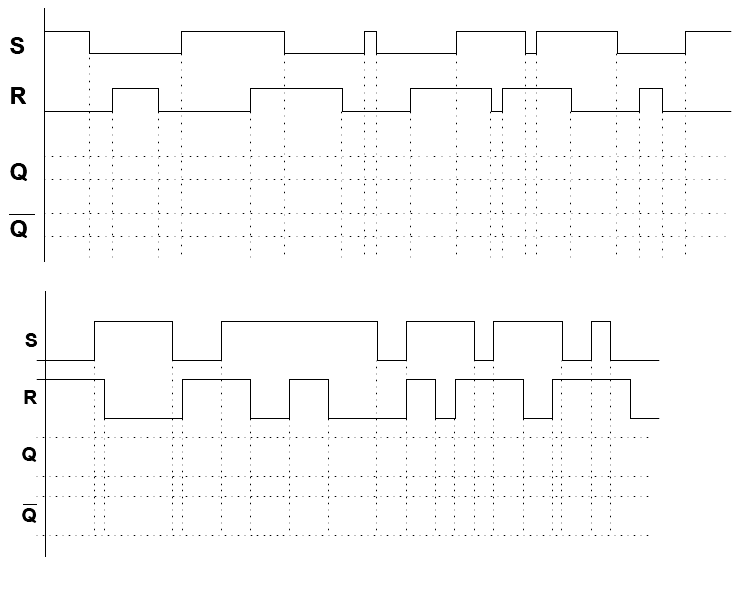
- Complete os diagramas de tempo dos latches SR Assíncronos:
Outras implementações do ff SR
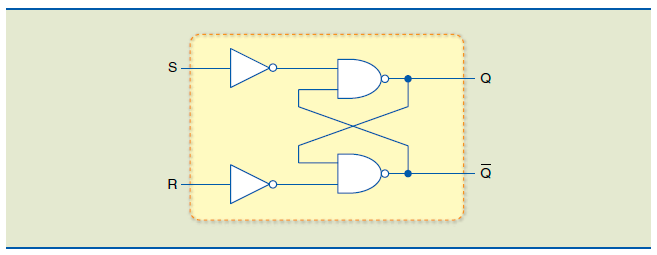
Existem outras implementações do SR, como os que utilizam portas NAND-NOT, ou apenas portas NAND.
Este circuito, cujas equações são Qi = (S'.Q'i-1)' e Q'i = (R'.Qi-1)' tem funcionamento idêntico ao anterior, com a mesma TV:
- S = R = 0 - mantém:
Qi = (0'.Q'i-1)' = (1.Q'i-1)' = (Q'i-1)' = Qi-1 Q'i = (0'.Qi-1)' = (1.Qi-1)' = (Qi-1)' = Q'i-1
- S = 0 e R = 1 - reseta:
Q'i = (1'.Qi-1)' = (0.Qi-1)' = (0)' = 1 => Qi = (0'.1)' = (1.1)' = (1)' = 0
- S = 1 e R = 0 - seta:
Qi = (1'.Q'i-1)' = (0.Q'i-1)' = (0)' = 1 => Q'i = (0'.1)' = (1.1)' = (1)' = 0
- S = 1 e R = 1 - condição inválida:
Qi = (1'.Q'i-1)' = (0.Q'i-1)' = (0)' = 1 Q'i = (1'.Qi-1)' = (0.Qi-1)' = (0)' = 1
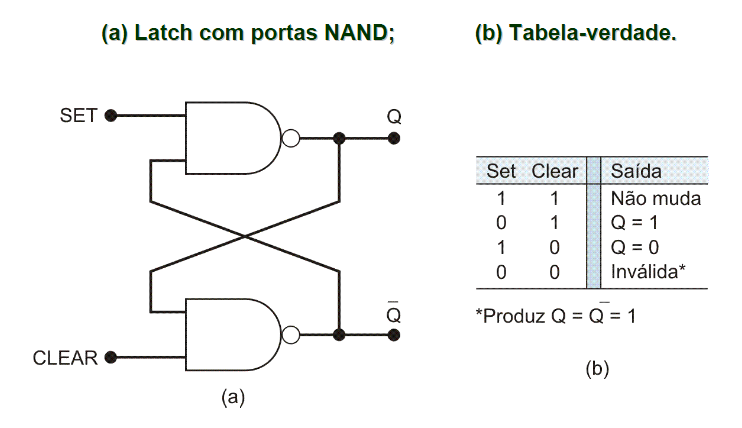
Já o circuito abaixo, é o dual do SR implementado a partir de portas NOR:
Aplicações dos FF SR Assíncronos
Temos diversas aplicações para os Latches RS Assíncronos.
De imediato vamos ver apenas dois exemplos:
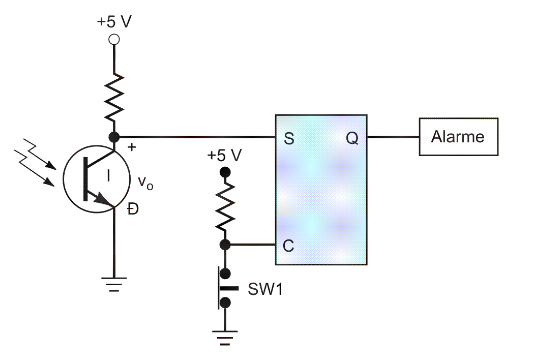
Acionamento de alarme
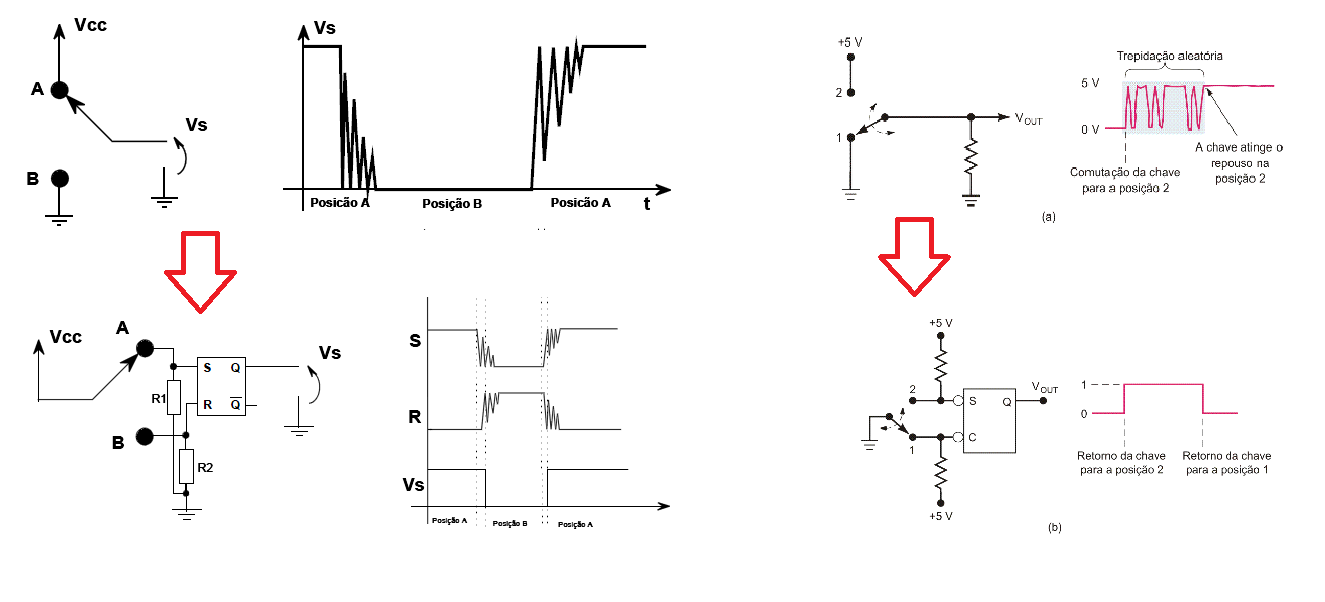
Chave anti rebote
Uma chave elétrica sempre apresenta ruídos quando fazemos a comutação devido ao atrito entre os contatos.
Este ruído é extremamente indesejável quando se trata de circuitos digitais ou até mesmo circuitos de audio e outros quaisquer.
Associando um Latch RS Assíncrono como mostra o circuito abaixo, eliminamos completamente este problema:
Os latches assíncronos são muito utilizados em circuitos lógicos, mas frequentemente é necessário que a dimensão tempo seja considerada nestes circuitos, para que os mesmos funcionem adequadamente.
Daremos, então, particular ênfase agora ao FF SR síncrono, isto é, aquele que recebe também um sinal de clock como entrada.
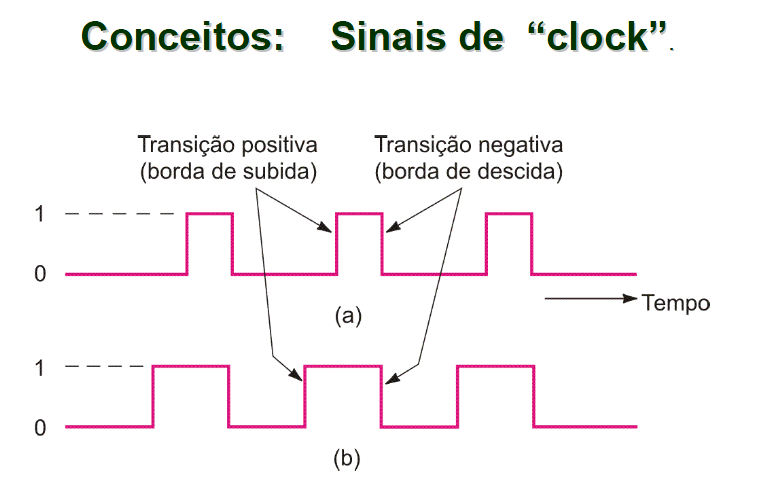
Sinal de Clock
O sinal de clock (relógio) é um sinal, normalmente uma onda quadrada periódica, que é utilizada para temporizar circuitos lógicos.
Normalmente, os circuitos respondem ao nível (0 ou 1), à subida (transição do nível 0 para o nível 1) do clock, ou à descida (transição do nível 1 para o nível 0), ou a ambos.
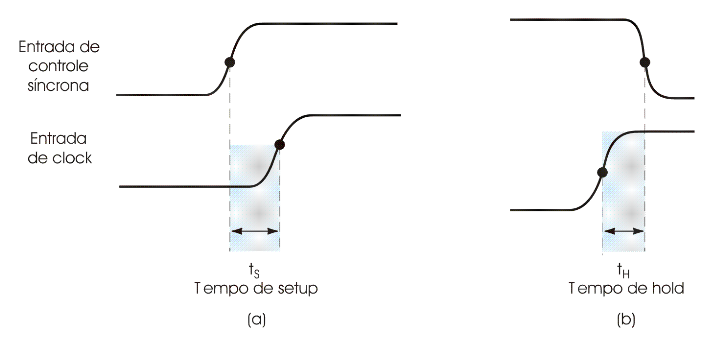
Além disto, a resposta não é imediata.
Entradas de controle tem de ser mantidas estáveis por: (a) um tempo tS antes da transição ativa do clock, e por (b) um tempo tH após a transição ativa do clock.
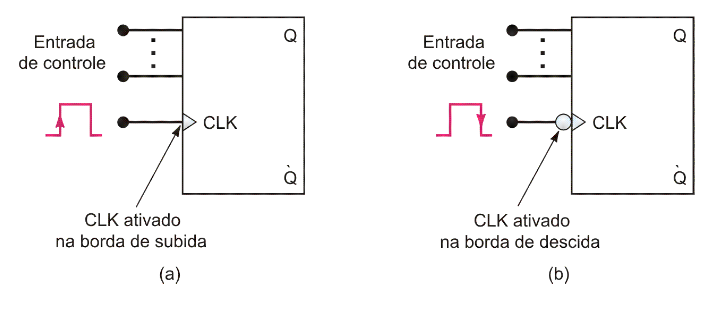
Esses dispositivos são conhecidos pela terminologia “disparados por borda” (do sinal de relógio) e podem ser de dois tipos:
- Disparados por borda de subida (transição positiva do sinal de clock): sensíveis às transições de nível lógico do sinal de clock, de “0” para “1”.
- Disparados por borda de descida (transição negativa do sinal de clock): sensíveis às transições de nível lógico do sinal de clock, de “1” para “0”.
Da mesma forma, flip-flops com clock, têm uma entrada de clock (CLK) que pode ser ativada por (a) uma borda de subida ou (b) por uma borda de descida.
As entradas de controle determinam o efeito da transição ativa do clock.
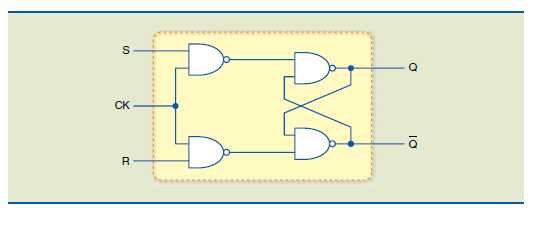
Circuito do SR Síncrono
Para que o flip-flop SR básico seja controlado por uma seq?uência de pulsos de clock, basta trocarmos os dois inversores do SR NAND-NOT por outras duas portas NAND, e nas outras entradas destas portas, injetarmos o clock.
O circuito ficará, então:
Quando a entrada clock assumir o valor 1, o circuito irá comportar-se como um FF SR básico:
| CLK | Qi |
|---|---|
| 0 | Qi-1 |
| 1 | SR básico |
Teremos então, a seguinte tabela verdade:
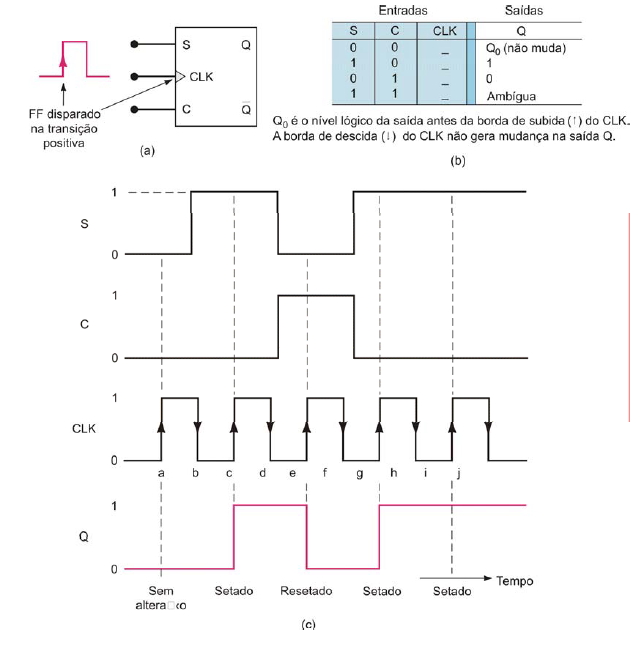
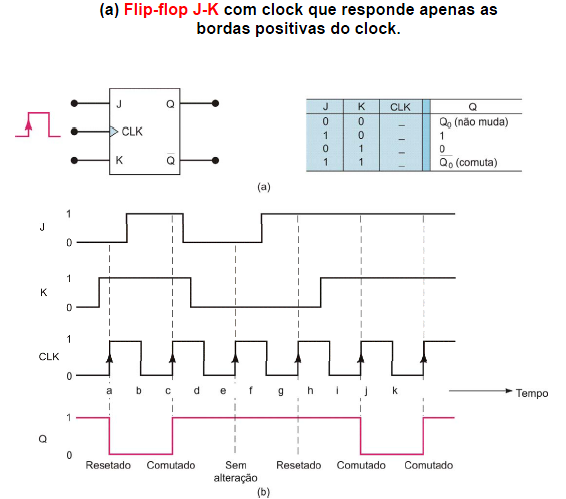
(a) Flip-flop S-C com disparo que responde apenas à borda positiva do pulso de clock; (b) tabela-verdade; (c) forma de ondas típicas.
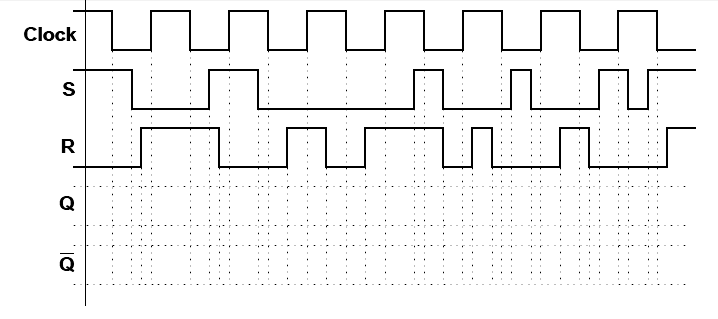
Exercícios propostos
- Complete o diagrama de tempo do latch SR Síncrono sensível ao nível 0:
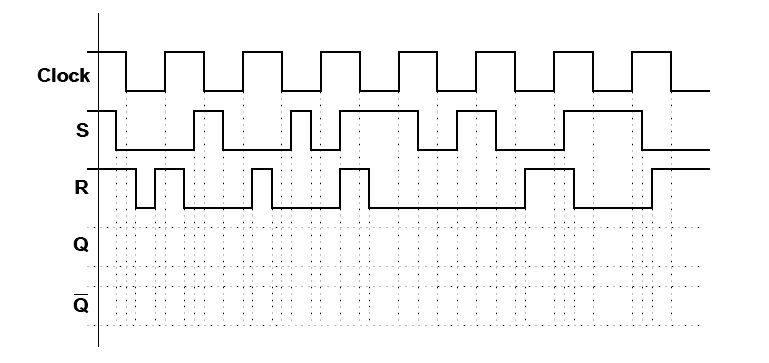
- Complete o diagrama de tempo do latch SR Síncrono sensível ao nível 1:
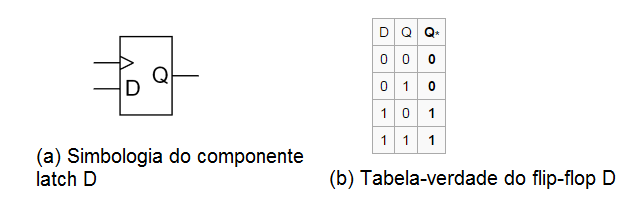
Flip-Flop do tipo D
O flip-flop D (data ou dado, pois armazena o bit de entrada) possui uma entrada, que é ligada diretamente à saída quando o clock é mudado.
Independentemente do valor atual da saída, ele irá assumir o valor 1, se D = 1 quando o clock for mudado ,ou o valor 0, se D = 0 quando o clock for mudado.
Este flip-flop pode ser interpretado como uma linha de atraso primitiva ou um hold de ordem zero, visto que a informação é colocada na saída um ciclo depois de ela ter chegado na entrada.
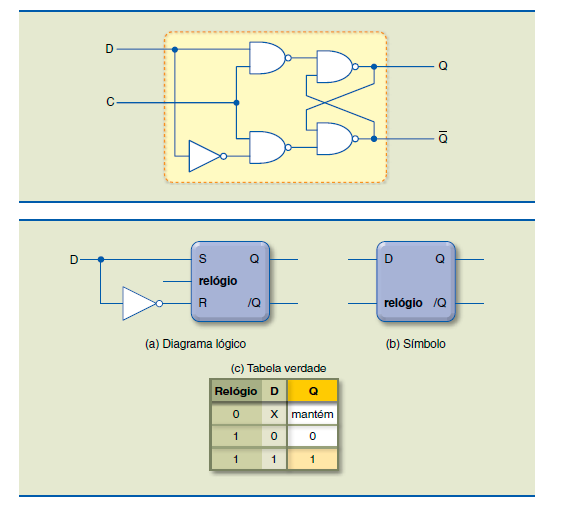
Um latch controlado (tipo D) é implementado colocando-se um inversor entre os terminais S e R de um latch RS.
Nessa configuração, impede-se que as variáveis de entrada assumam valores idênticos, isto é, S = R = 0 ou S = R = 1.
Assim, a entrada D também passa a ser única, e os pontos correspondentes a S e R, a assumir sempre valores distintos:
- Se D = 1, então S = 1 e R = 0 e Qi = 1
- Se D = 0, então S = 0 e R = 1 e Qi = 0
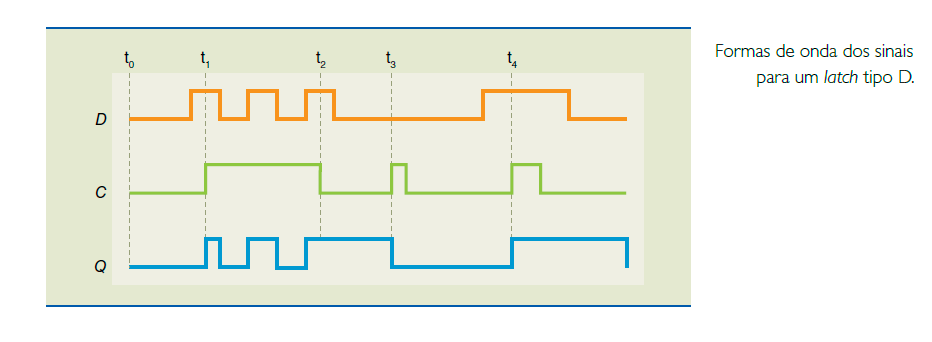
As formas de onda dos sinais para um latch tipo D são apresentadas na figura abaixo, em que:
- D é a entrada de dados;
- C, o sinal de habilitação ou clock;
- Q, a saída do latch.
Flip-Flop do tipo JK
As palavras SET e RESET significam, em relação a latches e Flip-Flops, armazenar nível lógico 1 e armazenar nível lógico 0, respectivamente.
Este fato nos dá margem a concluir que jamais poderíamos ativar os dois sinais simultaneamente, pois não existe um nível lógico que seja 0 e 1 ao mesmo tempo.
O Flip-Flop JK tem para o J a mesma função do SET e para o K a mesma do RESET e permite que ativemos os dois simultaneamente, e se fizermos isso ele complementa o nível lógico que está armazenando.
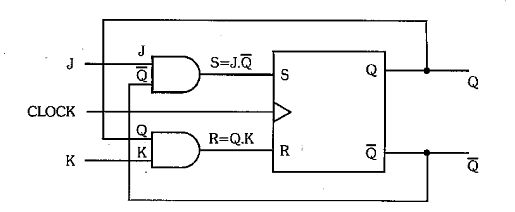
Analise o esquema abaixo:
Análise do Funcionamento do FF JK
O ff JK nada mais é do que um SR realimentado como mostra a figura acima, no qual:
S = J.Q'i-1
e
R = K.Qi-1
, o que determinam as entradas do FF SR interno.
A TV deste circuito é dada por:
| J | K | Qi-1 | Q'i-1 | S | R | Qi |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 | Qi-1 |
| 0 | 0 | 1 | 0 | 0 | 0 | Qi-1 |
| 0 | 1 | 0 | 1 | 0 | 0 | Qi-1 (=0) |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 0 | Qi-1 (=1) |
| 1 | 1 | 0 | 1 | 1 | 0 | Q'i-1 (=1) |
| 1 | 1 | 1 | 0 | 0 | 1 | Q'i-1 (=0) |
A tv simplificada para o FF JK fica, portanto:
| J | K | Qi |
|---|---|---|
| 0 | 0 | Qi-1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | Q'i-1 |
Em resumo, a condição inaceitável do SR, de S=R=1 agora é permitida no JK e fornece como saída atual, a saída anterior barrada.
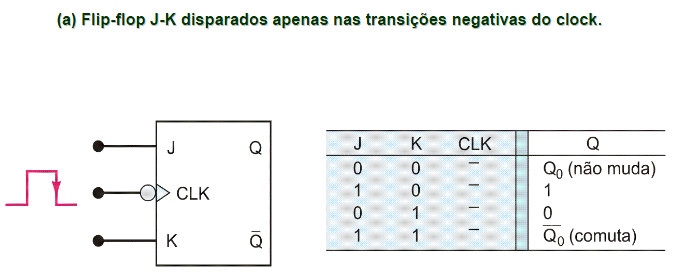
A simbologia dos FF JK e um diagrama de tempo são ilustrados abaixo:
Flip-Flop do tipo JK Mestre-Escravo
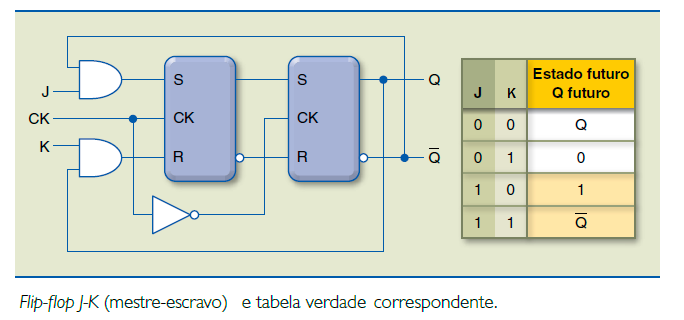
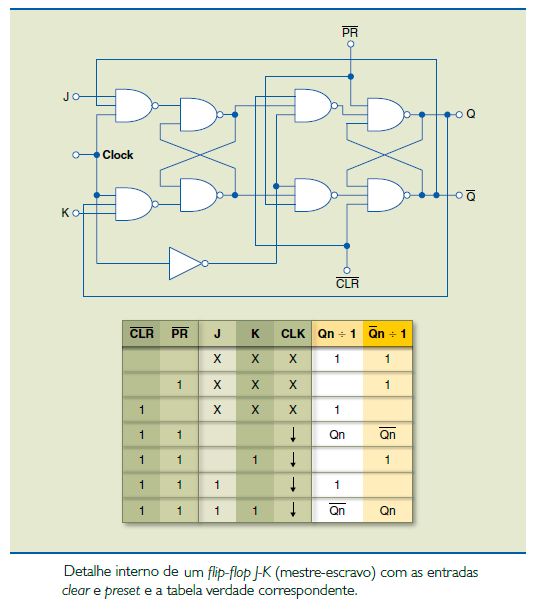
Esse dispositivo também possui duas entradas de dados (J e K) e tem como característica principal seus dois estágios internos, denominados mestre e escravo (figura abaixo) com a tabela verdade correspondente.
Análise do Funcionamento do FF JK MS
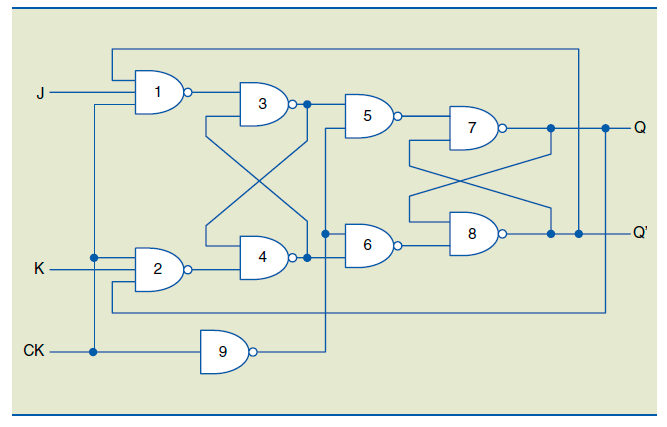
A figura abaixo mostra o circuito interno do FF JK MS:
Analisando a figura 4.11, podemos notar que:
- Se J = 0 e K = 0, as portas 1 e 2 estarão desabilitadas; portanto, após a aplicação do pulso de clock, o flip-flop não mudará de estado.
- Se J = 1 e K = 0 e Q = 0, a porta 1 habilitará (J = 1 e Q’ = 1) e a porta 2 desabilitará (K = 0 e Q = 0); portanto, após a aplicação do pulso de clock, o estado de saída Q mudará para Q = 1.
- Se J = 1 e K = 0 e Q = 1, a porta 1 desabilitará (J = 1 e Q’ = 0) e a porta 2 desabilitará (K = 0 e Q = 1); portanto, após a aplicação do pulso de clock, o estado de saída permanecerá inalterado (Q = 1).
- Se J = 0 e K = 1 e Q = 0, a porta 1 desabilitará (J = 0 e Q’ = 1) e a porta 2 desabilitará (K = 1 e Q = 0); portanto, após a aplicação do pulso de clock, o estado de saída permanecerá inalterado (Q = 0).
- Se J = 0 e K = 1 e Q = 1, a porta 1 desabilitará (J = 0 e Q’ = 0) e a porta 2 habilitará (K = 1 e Q = 1); portanto, após a aplicação do pulso de clock, o estado de saída Q mudará para Q = 0.
- Se J = 1 e K = 1, para J = K = 1, a cada ciclo de clock o estado do flip-flop J-K se complementa; portanto, após a aplicação do sinal de clock, teremos:
- se Q = 0, a saída Q mudará para Q = 1;
- se Q = 1, a saída Q mudará para Q = 0.
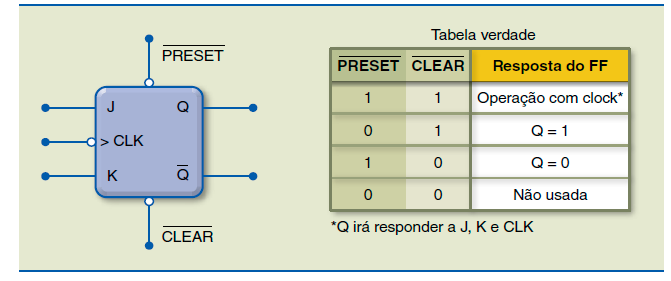
Flip-Flop JK com Preset e Clear
Podemos também incluir as entradas de preset e clear nesse circuito, que passa a ter a configuração da figura abaixo. A tabela verdade inclui as entradas de preset (PR) e clear (CLR).
Simbologia do JK com Preset e Clear e TV
A figura abaixo mostra a simbologia do FF JK com Preset e Clear:
<<< Voltar para página principal do curso
| << Famílias Lógicas | AULA 17 - Flip-Flops |
|---|