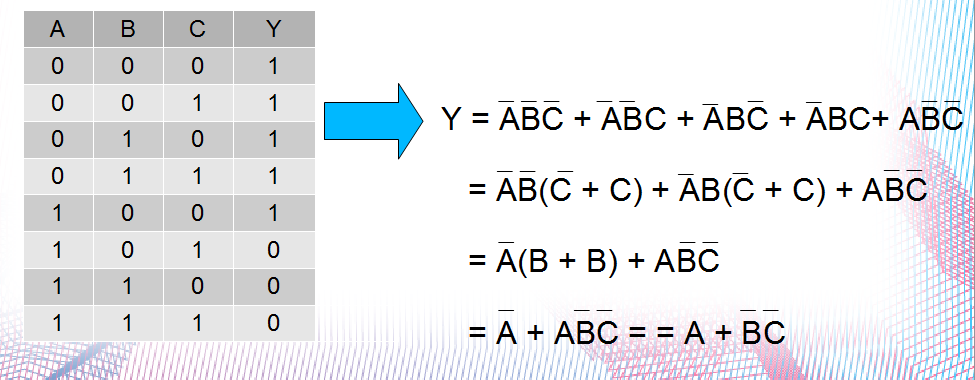AULA 11 - Eletrônica Digital 1 - Graduação
Projeto de Circuitos Combinacionais
Um circuito combinacional é aquele constituído por um conjunto de portas lógicas, as quais determinam (pelas EQUAÇÕES BOOLEANAS) os valores das saídas diretamente a partir dos valores atuais das entradas.
Ao contrário dos circuitos sequenciais, não há alteração dos estados do circuito, como função do tempo.
O presente capítulo refere-se ao raciocínio, método e ferramentas utilizados para se fazer o projeto de circuitos combinacionais, a partir de uma especificação do que se pretende obter.
Especificação
Passos para montagem de um circuito combinacional:
- Determinar as representações (símbolo/letra) para cada variável de entrada e saída;
- Identificação do problema (Tabela-Verdade);
- Determinação das equações lógicas simplificadas;
- Verificar quais componentes comerciais podem ser utilizados;
- Desenhar o circuito final.
Exemplo 1:
Projetar o circuito que recebe um inteiro binário de 3 bits e determina se este número é menor ou igual a 4.
O primeiro passo é pensar no que seria(m) a(s) entrada(s) e saída(s) do circuito!???
O fato de ser um “número binário de 3 bits” nos indica:
- que a entrada será um inteiro binário (como deve ser, em sistemas digitais! ;) );
- os números que podem entrar neste circuito variam entre 0 e 7 (3 bits);
- a entrada será composta por 3 pinos, cada um para um destes bits, que chamaremos de A, B e C.
Quanto à saída: ela deverá “indicar”, de alguma maneira, se o número que entrou em ABC é, ou não, menor ou igual à 4.
Em circuitos digitais, esta indicação pode ser dada, simplesmente, por um valor alto na saída (1), quando houver detecção, ou um valor baixo (0), quando não houver!
Em outras palavras, se entrar algum número entre 0 e 4, a saída deverá ser 1. Caso contrário, deverá ser 0!
Se o circuito “recebe” um inteiro, então esta é a entrada esperada do circuito → um número inteiro!
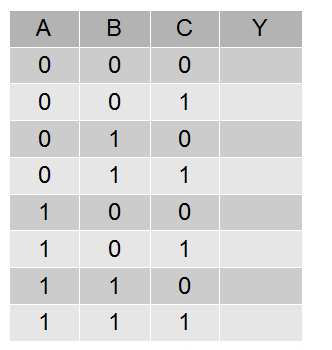
O segundo passo é montar a tabela-verdade, que vai se parecer com:
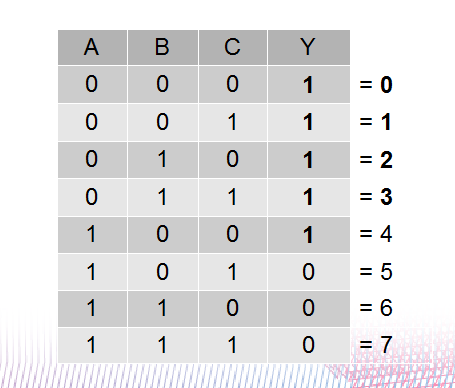
A saída esperada é que o circuito detecte valores de entradas menores ou iguais a 3.
Então, na TV, as saídas Y deverão ser “1” apenas para os 4 primeiros valores:
Desta forma:
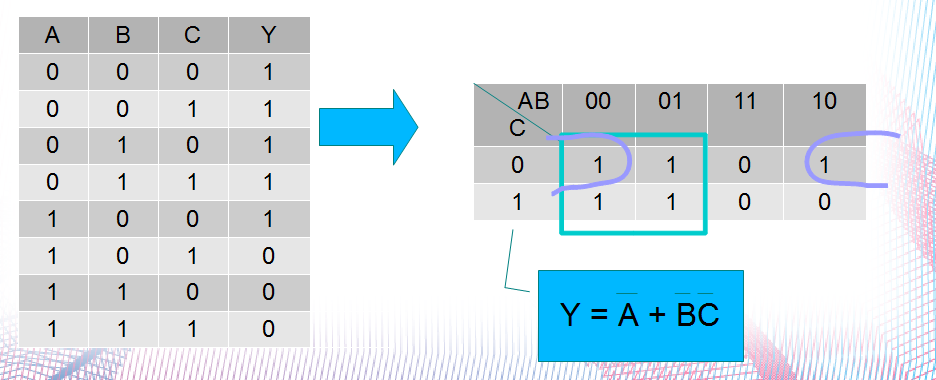
Para começar o 3o. Passo, você precisa agora, converter a TV em uma equação lógica booleana ou Mapa de Karnaugh e minimizar o número de componentes!
ou:
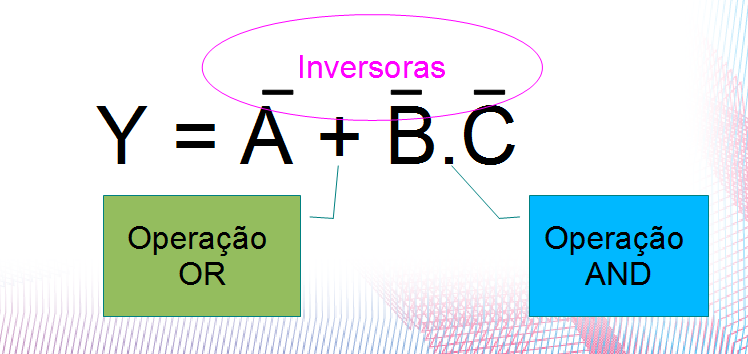
No quarto passo, verificaremos como podemos especificar o circuito que melhor se adequará à equação booleana resultante.
Verificamos que a saída desejada limita-se à entrada A invertida mais as entradas B e C, também invertidas, jogadas como entradas de uma porta E !!
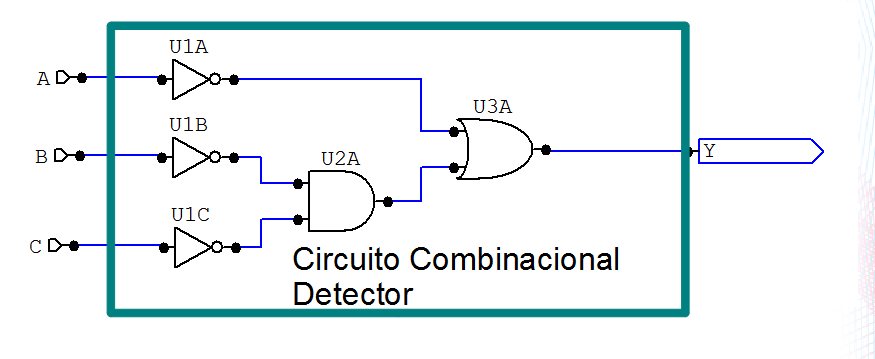
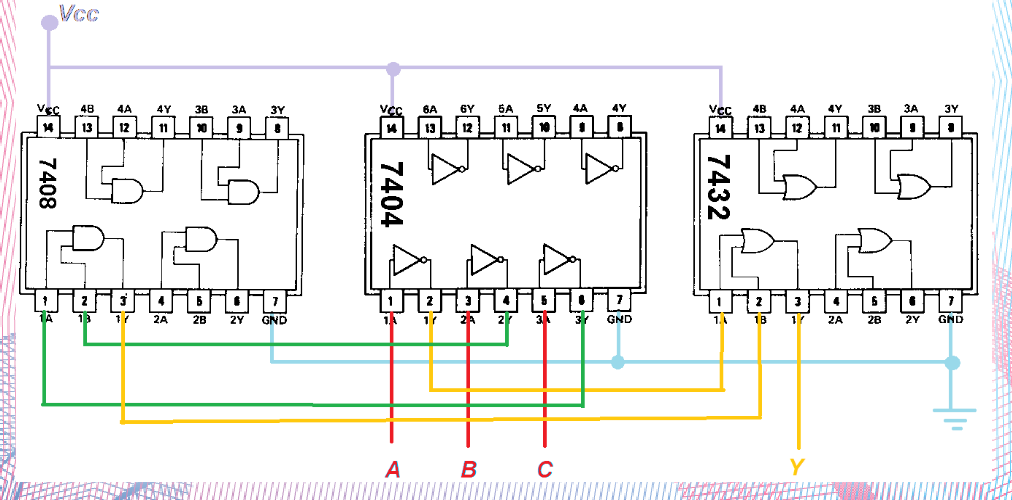
Por fim, chegamos ao último passo:
Esquema de interligação dos CIs:
Exercícios:
- Se o problema restringisse que só poderíamos usar portas NAND (NÃO-E) e OR (OU) na construção deste circuito, como você faria?
- Se o problema pedisse que a saída Y também detectasse quando todas as entradas fossem 1, que alteração(ões) você faria no circuito?