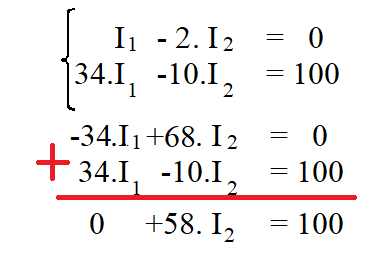AULA 10 - Eletricidade Básica - FIC

De IFSC
Revisão de 10h59min de 29 de setembro de 2022 por imported>Fargoud (→‎Exemplo 3: Análise de Malhas para circuito misto 2)
Ir para navegação Ir para pesquisar


CARGA HORÁRIA: 5 h

CARGA HORÁRIA TEÓRICA: 3 h CARGA HORÁRIA PRÁTICA: 2 h


METODOLOGIA

  • Exposição dialogada dos conteúdos disponíveis, em projetor multimídia.
  • Navegação assistida em outros sites e portais, de conteúdos relacionados.
  • Montagens práticas e desenvolvimento em computador de aplicativos.
  • Testes de verificação e validação.




Circuitos Mistos

Apesar de termos estudado apenas circuitos compostos por uma única malha, ou um único par de nós, a imensa maioria dos circuitos é composta por uma combinação de malhas e nós.

Ao circuito em que existem resistências, tanto em série como em paralelo, é dado o nome de circuito misto.

Existem várias maneiras de se resolver um circuito misto.

Podem ser utilizadas as Leis de Kirchoff, ou análise das redes resistivas e Lei de Ohm.


Exemplo 1:

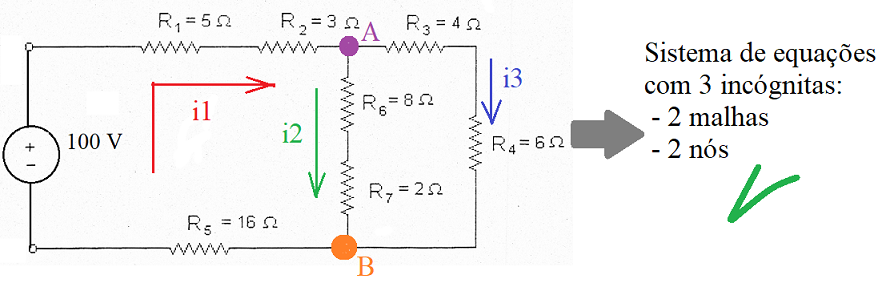
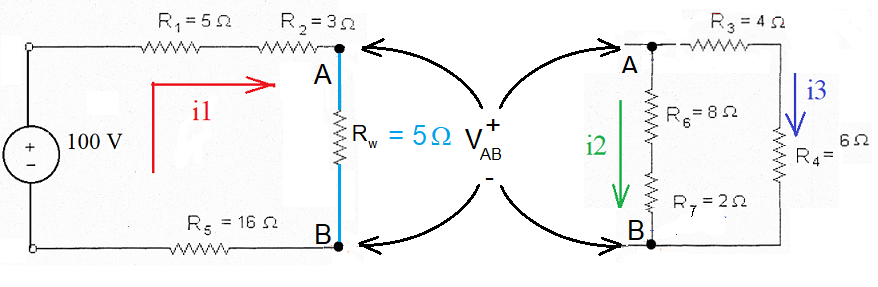
Determine as correntes nos ramos do circuito abaixo:

Circmistoex1.png

Uma maneira de resolver é:

1) Primeiramente, inspecionar quantos nós e quantas malhas tem o circuito. Observamos que o circuito tem 2 malhas e 1 nó independente (A)*, ou seja, 3 equações a serem levantadas.

2) Em seguida, arbitra-se uma corrente para cada um dos ramos. O sentido da corrente não importa porque, caso tenha sido arbitrado errado, ao final do equacionamento o valor da corrente dará negativo, indicando que o sentido era o outro. O circuito tem 3 ramos principais, o que significa que temos 3 correntes (incógnitas) a serem calculadas. 

Um circuito que tenha número de equações maior ou igual ao número de incógnitas de tensão e corrente pode ser calculado!

3) Então, aplica-se a Lei de Kirchoff das Tensões à cada uma das malhas do circuito. Isto significa definir um "ponto de partida" e ir percorrendo a malha (no sentido horário, ou antihorário), somando cada tensão de fonte ou parcela de resistor multiplicado pela corrente do ramo, à equação da malha. Quando o percurso "encontrar" o sinal negativo da fonte, esta parcela entra como negativa na equação, e vice-versa. Quando o percurso "encontrar" a corrente de frente (que está vindo, portanto, do sentido contrário), esta parcela entra como negativa na equação, e vice-versa. No presente circuito, devemos, então, levantar as 2 equações de malha.

4) Por fim, aplica-se a Lei de Kirchoff das Correntes a cada um dos nós do circuito. Sempre observando a convenção (corrente entrando no nó é adicionada como positiva e corrente saindo, como negativa). Neste circuito, devemos analisar o nó A*.

Assim:

Malha 1:

R5.I1 - 100 + R1.I1 + R2.I1 + R6.I2 + R7.I2 = 0

16.I1 - 100 + 5.I1 + 3.I1 + 8.I2 + 2.I2 = 0

(16 + 5 + 3).I1 + (8 + 2).I2 = 100

24.I1 + 10.I2 = 100 (Equação I)

Malha 2:

-R7.I2 - R6.I2 + R3.I3 + R4.I3 = 0

-2.I2 - 8.I2 + 4.I3 + 6.I3 = 0

-10.I2 + 10.I3 = 0

10.I3 = 10.I2

I3 = I2 (Equação II)

Nó A:

+I1 - I2 - I3 =0

I1= I2 + I3 (Equação III) 

* Note que o somatório das correntes no nó B seria igual ao somatório no nó A

e dado por: 

-I1 + I2 + I3 =0

I2 + I3 = I1 

  Ou seja, o nó B não é independente do nó A, e seu equacionamento não acrescenta informação ao circuito!!!

Substituindo-se (II) em (III):

I1 = I2 + (I2)

I1 = 2.I2 (Equação IV)

Substituindo-se (IV) em (I):

24.I1 + 10.I2 = 100

24.(2.I2) + 10.I2 = 100

48.I2 + 10.I2 = 100

58.I2 = 100

I2 = 100/58

I2 = I3 = 1,72 A (Equação V)

Por fim, substituindo-se (V) em (IV): 

I1 = Ifonte = 3,44 A


Além do método de inspeção e aplicação das Leis de Kirchoff, o circuito resistivo normalmente pode ser resolvido pela resolução das redes resistivas e aplicação da Lei de Ohm, como segue:

====================================

Exemplo 2:

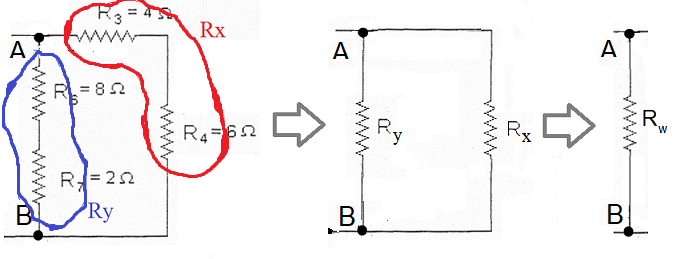
Outra maneira de resolver este circuito, é pela resolução das resistências equivalentes:

Equiv1-1.png

Fazendo Rx = R3 + R4 e Ry = R6 + R7, teremos:

Rx = 4 + 6 = 10 Ω

Ry = 8 + 2 = 10 Ω

Portanto, o equivalente do paralelo Rw = Rx//Ry:

Rw = (10.10)/(10 + 10) = 100/20

→ Rw = 5 Ω

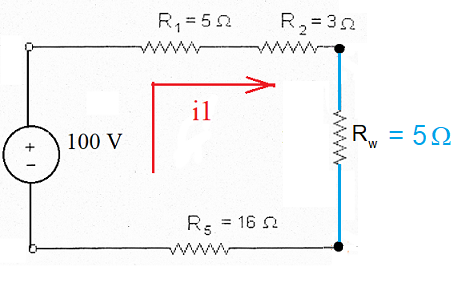
Agora fica mais fácil encontrar a corrente da fonte porque, uma vez resolvido o paralelo, o circuito fica reduzido a um circuito série:

Equiv2.png

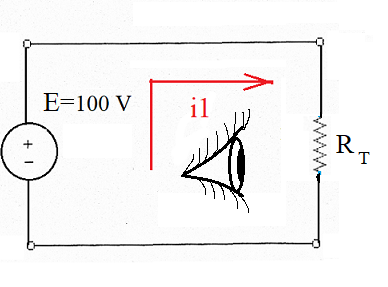
Ou, sob o ponto de vista da fonte:

Equival4.png

E a corrente da fonte I1 será dada por:

I1 = E/(RT )

, onde RT = R1 + R2 + Rw + R5 = 5 + 3 + 5 + 16 = 29 Ω

I1 = 100/29

→ I1 = 3,45 Ω

Ora, agora para calcular as correntes individuais Isub>2 e Isub>3 do paralelo, basta calcular qual a tensão VAB, a qual será dada por:

VAB = Rw.I1 = 5. 3,45 = 17,24 V

Equival3.png

Esta tensão, obviamente, será igual à

VAB = (R6 + R7).I2 e a

VAB = (R3 + R4).I3

Assim, a corrente I2 será dada por:

I2 = VAB/(R6 + R7) = 17,24/(8 + 2)

I2 = 17,24/10 → I2 = 1,72 A

E a corrente I3, por sua vez, será dada por:

I3 = VAB/(R3 + R4) = 17,24/(4 + 6)

I3 = 17,24/10 → I3 = 1,72 A

Como quisemos demonstrar!!!!!!

Exercício 1

Resolva o circuito abaixo utilizando as Leis de Kirchoff e Lei de Ohm:

Circmisto1.png

Solução do Exercício de Leis de Kirchoff

Análise de Malhas Generalizada

Os métodos de análise por inspeção, que utilizam Leis de Kirchoff e Lei de Ohm são bastante eficientes, mas dependem muito da expertise do profissional que está analisando o circuito.

A análise de malhas generalizada é um método sistemático que permite analisar qualquer circuito, através das suas correntes internas.

Não depende de identificar qual(is) o(s) melhor(es) equacionamento(s), mas apenas da aplicação correta do método

O método consiste nos seguintes passos:


.

→ Para cada malha, faça:
  1. Arbitre uma corrente elétrica percorrendo toda aquela malha, e não para os ramos individuais, como fazíamos;
  2. Seguindo o sentido desta corrente, compute o somatório das tensões (fontes e quedas de tensões nos resistores) da seguinte maneira:
    1. A tensão da fonte de tensão será dada pelo valor da fonte e o sinal de entrada da corrente na fonte;
    2. Em ramos isolados, a queda de tensão será dada por R.Ix, onde Ix é a corrente daquela malha;
    3. Em ramos comuns a duas malhas, a queda de tensão será dada por R.(Ix - Iy), onde Ix é a corrente daquela malha, e Iy, a corrente da outra malha;
    4. Em fontes de corrente, arbitre uma tensão e depois utilize o valor da fonte para determinar a corrente naquele ramo;
  3. Iguale o somatório a zero.
→Repita o procedimento para as demais malhas.
→Resolva o sistema de equações por substituição, ou inversão de matrizes e encontre as correntes das malhas.
→As correntes dos ramos comuns à duas malhas serão calculados como a diferença entre as correntes de malhas.
→Determine as tensões de interesse.


 * Você pode escolher o sentido horário, ou antihorário, porque, caso o sentido inicial tenha sido arbitrado errado, o sinal da corrente resultará em negativo, indicando que o sentido é o inverso. PORÉM, é extremamente recomendável que o sentido arbitrado para TODAS AS CORRENTES seja O MESMO: ou horário, ou anti-horário, sob pena de duas correntes terem seus sentidos arbitrados errado, e o erro de uma anular o erro da outra.

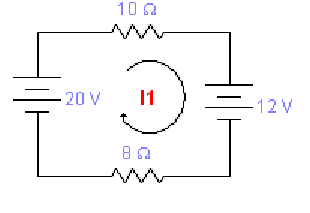
Exemplo 1: Análise de Malhas para circuito série

Analmalhas2.png

Como este circuito só contém uma malha, a análise se dará como segue:

1) Arbitre uma corrente elétrica percorrendo toda aquela malha 

→ Ok! Arbitrada a corrente I1;

2) Seguindo o sentido desta corrente, compute o somatório das tensões. 

→ -20 + 10.I1 +12 +8.I1 = 0

3)Resolva a equação. 

→ 18.I1 = 20 - 12 → 18.I1 = 8 → I1 = 8/18 

 → I1 = 0,44 A

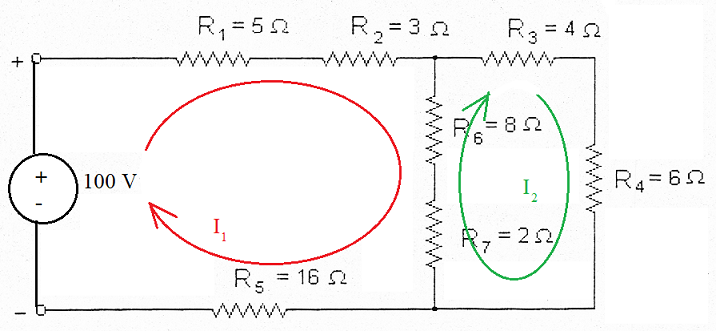
Exemplo 2: Análise de Malhas para circuito misto 1

Analmalhas3.png

Este circuito contém duas malhas, então, a análise se dará como segue:

1) Arbitre uma corrente elétrica em cada malha 

→ Ok! Arbitradas as correntes I1 e I2;

2.1) Seguindo o sentido da corrente I1, compute o somatório das tensões na malha 1:

- 100 + R1.I1 + R2.I1 + R6.(I1 -I2) + R7.(I1 -I2) + R5.I1 = 0

Ou seja:

- 100 + 5.I1 + 3.I1 + 8.(I1 -I2) + 2.(I1 -I2) + 16.I1 = 0

- 100 + 8.I1 + 8.I1 -8. I2 + 2.I1 -2. I2 + 16.I1 = 0

- 100 + 34.I1 -10. I2 = 0 

34.I1 -10.I2  = 100 (Equação I)

2.2) Seguindo o sentido da corrente I2, compute o somatório das tensões na malha 2:

R7.(I2 -I1) + R6.(I2 -I1) + R3.I2 + R4.I2 = 0

Ou seja:

2.(I2 -I1) + 8.(I2 -I1) + 4.I2 + 6.I2 = 0

2.I2 - 2.I1 + 8.I2 -8.I1 + 4.I2 + 6.I2 = 0

- 10.I1 + 20.I2 = 0

20.I2 = 10.I1 


2.I2 = I1 (Equação II)


3)Resolva o sistema de equações 

→ 34.I1 -10.I2  = 100 

 → 2.I2 = I1

Existem várias maneiras de se resolver um sistema de equações. Por exemplo:

3.1) Por substituição:

Fazendo I1 = 2.I2 e substituindo-se em: 34.I1 -10.I2 = 100, teremos:

34.(2.I2) - 10.I2 = 100

68.I2 - 10.I2 = 100

58.I2 = 100

I2 = 100/58

I2 = 1,72 A

E, por consequência:

I1 = 2.I2

I1 = 2.1,72

I1 = 3,44 A

3.2) Resolvendo o sistema de equações por soma:

Sistequ1.png

E, assim por diante.

4) A corrente I3 será dada por I1 - I2 , portanto, 3,44 - 1,72 = 1,72 A


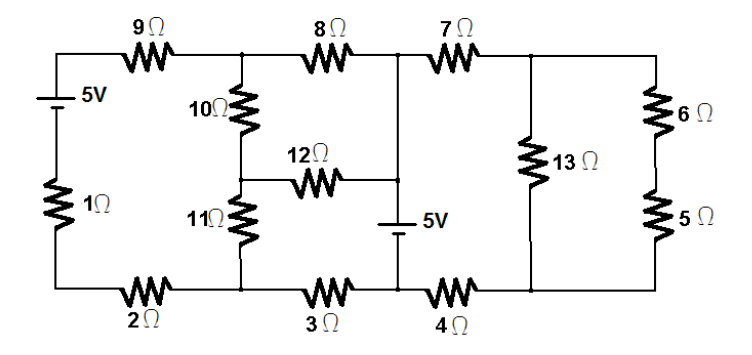
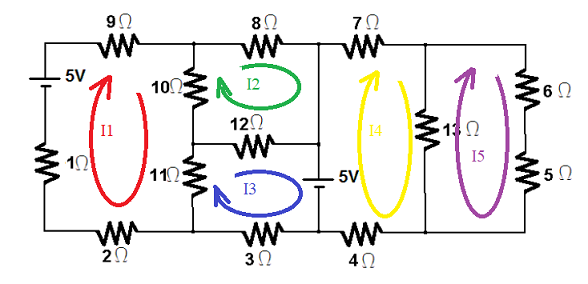
Exemplo 3: Análise de Malhas para circuito misto 2

Analmalhas5.png

Este circuito contém duas malhas, então, a análise se dará como segue:

1) Arbitre uma corrente elétrica em cada malha


Analmalhas5-1.png


2.1) Seguindo o sentido da corrente I1, compute o somatório das tensões na malha 1:

2.I1 + 1.I1 -5 + 9.I1 + 10.(I1 - I2) + 11.(I1 -I3) = 0

33.I1 - 22.I2 = 5 (Equação I)

2.2) Seguindo o sentido da corrente I2, compute o somatório das tensões na malha 2:

10.(I2 -I1) + 8.I2 + 12.(I2 - I3 = 0

- 10.I1 + 30.I2 - 12.I3) = 0(Equação II)


2.3) Seguindo o sentido da corrente I2, compute o somatório das tensões na malha 3:

11.(I3 -I1) + 12.(I3 -I2) +5 + 3.I3 = 0

- 11.I1 -12.I2 +26.I3 = -5(Equação II)


2.4) Seguindo o sentido da corrente I2, compute o somatório das tensões na malha 4:

10.(I2 -I1) + 8.I2 + 12.(I2 - I3) = 0

- 10.I1 + 30.I2 - 12.I3) = 0(Equação II)


2.5) Seguindo o sentido da corrente I2, compute o somatório das tensões na malha 5:

10.(I2 -I1) + 8.I2 + 12.(I2 - I3) = 0

- 10.I1 + 30.I2 - 12.I3) = 0(Equação II)



3)Resolva o sistema de equações 

→ 34.I1 -10.I2  = 100 

 → 2.I2 = I1

Existem várias maneiras de se resolver um sistema de equações. Por exemplo:

3.1) Por substituição:

Fazendo I1 = 2.I2 e substituindo-se em: 34.I1 -10.I2 = 100, teremos:

34.(2.I2) - 10.I2 = 100

68.I2 - 10.I2 = 100

58.I2 = 100

I2 = 100/58

I2 = 1,72 A

E, por consequência:

I1 = 2.I2

I1 = 2.1,72

I1 = 3,44 A

3.2) Resolvendo o sistema de equações por soma:

Sistequ1.png

E, assim por diante.

4) A corrente I3 será dada por I1 - I2 , portanto, 3,44 - 1,72 = 1,72 A

Fontes Bibliográficas

COMISSÃO TRIPARTITE PERMANENTE DE NEGOCIAÇÃO DO SETOR ELÉTRICO NO ESTADO DE SÃO PAULO - CPN. Eletricidade Básica - Manual de treinamento curso básico segurança em instalações e serviços com eletricidade - NR 10 . Disponível em: https://portalidea.com.br/cursos/9f2909192195f210d6c6fa89c0894301.pdf

Lemes, Andryos da Silva. APOSTILA DE ELETRICIDADE BÁSICA. MINISTÉRIO DA EDUCAÇÃO, IFSP - CAMPUS DE PRESIDENTE EPITÁCIO. Disponível em:https://pt.scribd.com/document/280039386/Apostila-Eletricidade-Basica

ROCHA, Helder da. Introdução à Eletrônica para Artistas. Apostila de curso livre. 2017. Disponível em: http://www.argonavis.com.br/cursos/eletronica/IntroducaoEletronicaArtistas.pdf.

SAMBAQUI, ANA BARBARA KNOLSEISEN; TAQUES, BÁRBARA OGLIARI. Apostila de Eletricidade. MINISTÉRIO DA EDUCAÇÃO - IFSC - CAMPUS JOINVILLE. Joinville, agosto, 2010. Disponível em: http://wiki.itajai.ifsc.edu.br/images/c/c1/Apostila_de_Eletricidade_IFSC_JOINVILE.pdf

Souza, Giovani Batista. ELETRICIDADE. MINISTÉRIO DA EDUCAÇÃO - IFSC - CAMPUS ARARANGUÁ. Edição: fev, 2009. Disponível em: https://wiki.sj.ifsc.edu.br/images/e/e6/Aru-2009-Agosto-eletricidade_basica.pdf


<<< Voltar para página principal do curso

Leis de Kirchoff << AULA 10 - ANÁLISE DE MALHAS Análise de Nós >>
Disponível em “https://wiki.ifsc.edu.br/index.php?title=AULA_10_-_Eletricidade_Básica_-_FIC&oldid=22321”