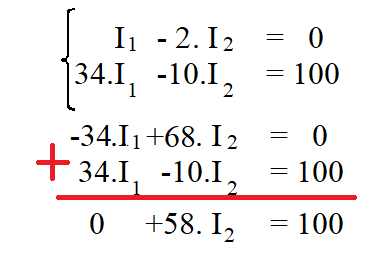AULA 10 - Eletricidade Básica - FIC

De IFSC
Revisão de 09h55min de 5 de outubro de 2022 por imported>Fargoud (→‎Análise Computacional de circuitos)
Ir para navegação Ir para pesquisar

<<< Voltar para página principal do curso



CARGA HORÁRIA: 5 h

CARGA HORÁRIA TEÓRICA: 4 h CARGA HORÁRIA PRÁTICA: 1 h


METODOLOGIA

  • Exposição dialogada dos conteúdos disponíveis, em projetor multimídia.
  • Navegação assistida em outros sites e portais, de conteúdos relacionados.
  • Montagens práticas e desenvolvimento em computador de aplicativos.
  • Testes de verificação e validação.




Circuitos Mistos

Apesar de termos estudado apenas circuitos compostos por uma única malha, ou um único par de nós, a imensa maioria dos circuitos é composta por uma combinação de malhas e nós.

Ao circuito em que existem resistências, tanto em série como em paralelo, é dado o nome de circuito misto.

Existem várias maneiras de se resolver um circuito misto.

Podem ser utilizadas as Leis de Kirchoff, ou análise das redes resistivas e Lei de Ohm.


Exemplo 1:

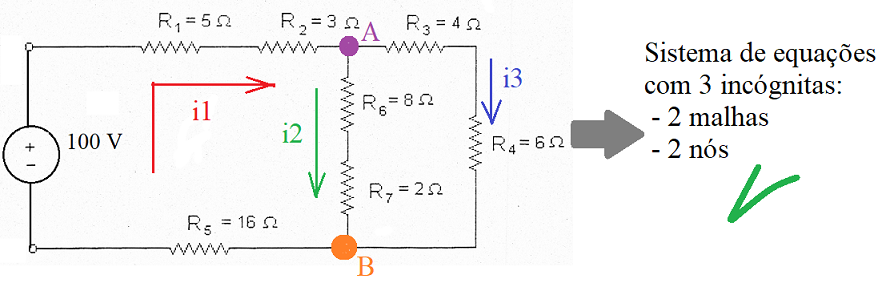
Determine as correntes nos ramos do circuito abaixo:

Circmistoex1.png

Uma maneira de resolver é:

1) Primeiramente, inspecionar quantos nós e quantas malhas tem o circuito. Observamos que o circuito tem 2 malhas e 1 nó independente (A)*, ou seja, 3 equações a serem levantadas.

2) Em seguida, arbitra-se uma corrente para cada um dos ramos. O sentido da corrente não importa porque, caso tenha sido arbitrado errado, ao final do equacionamento o valor da corrente dará negativo, indicando que o sentido era o outro. O circuito tem 3 ramos principais, o que significa que temos 3 correntes (incógnitas) a serem calculadas. 

Um circuito que tenha número de equações maior ou igual ao número de incógnitas de tensão e corrente pode ser calculado!

3) Então, aplica-se a Lei de Kirchoff das Tensões à cada uma das malhas do circuito. Isto significa definir um "ponto de partida" e ir percorrendo a malha (no sentido horário, ou antihorário), somando cada tensão de fonte ou parcela de resistor multiplicado pela corrente do ramo, à equação da malha. Quando o percurso "encontrar" o sinal negativo da fonte, esta parcela entra como negativa na equação, e vice-versa. Quando o percurso "encontrar" a corrente de frente (que está vindo, portanto, do sentido contrário), esta parcela entra como negativa na equação, e vice-versa. No presente circuito, devemos, então, levantar as 2 equações de malha.

4) Por fim, aplica-se a Lei de Kirchoff das Correntes a cada um dos nós do circuito. Sempre observando a convenção (corrente entrando no nó é adicionada como positiva e corrente saindo, como negativa). Neste circuito, devemos analisar o nó A*.

Assim:

Malha 1:

R5.I1 - 100 + R1.I1 + R2.I1 + R6.I2 + R7.I2 = 0

16.I1 - 100 + 5.I1 + 3.I1 + 8.I2 + 2.I2 = 0

(16 + 5 + 3).I1 + (8 + 2).I2 = 100

24.I1 + 10.I2 = 100 (Equação I)

Malha 2:

-R7.I2 - R6.I2 + R3.I3 + R4.I3 = 0

-2.I2 - 8.I2 + 4.I3 + 6.I3 = 0

-10.I2 + 10.I3 = 0

10.I3 = 10.I2

I3 = I2 (Equação II)

Nó A:

+I1 - I2 - I3 =0

I1= I2 + I3 (Equação III) 

* Note que o somatório das correntes no nó B seria igual ao somatório no nó A

e dado por: 

-I1 + I2 + I3 =0

I2 + I3 = I1 

  Ou seja, o nó B não é independente do nó A, e seu equacionamento não acrescenta informação ao circuito!!!

Substituindo-se (II) em (III):

I1 = I2 + (I2)

I1 = 2.I2 (Equação IV)

Substituindo-se (IV) em (I):

24.I1 + 10.I2 = 100

24.(2.I2) + 10.I2 = 100

48.I2 + 10.I2 = 100

58.I2 = 100

I2 = 100/58

I2 = I3 = 1,72 A (Equação V)

Por fim, substituindo-se (V) em (IV): 

I1 = Ifonte = 3,44 A


Além do método de inspeção e aplicação das Leis de Kirchoff, o circuito resistivo normalmente pode ser resolvido pela resolução das redes resistivas e aplicação da Lei de Ohm, como segue:

====================================

Exemplo 2:

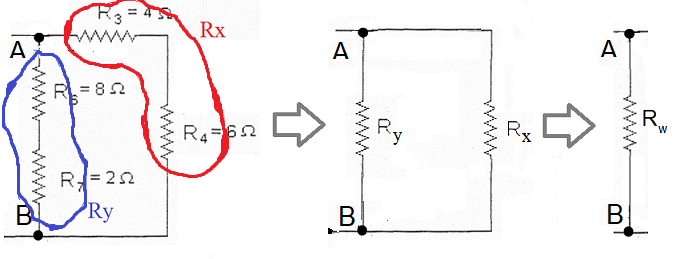
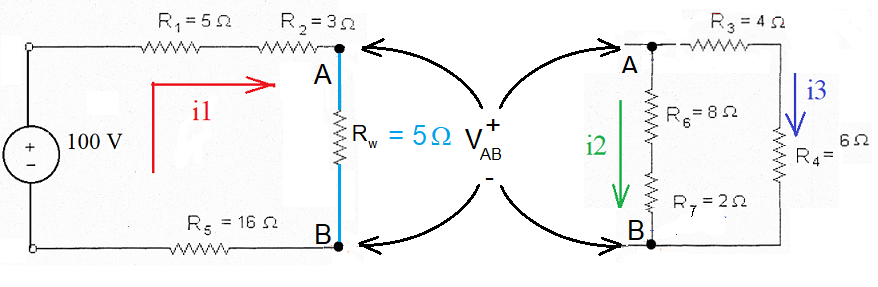
Outra maneira de resolver este circuito, é pela resolução das resistências equivalentes:

Equiv1-1.png

Fazendo Rx = R3 + R4 e Ry = R6 + R7, teremos:

Rx = 4 + 6 = 10 Ω

Ry = 8 + 2 = 10 Ω

Portanto, o equivalente do paralelo Rw = Rx//Ry:

Rw = (10.10)/(10 + 10) = 100/20

→ Rw = 5 Ω

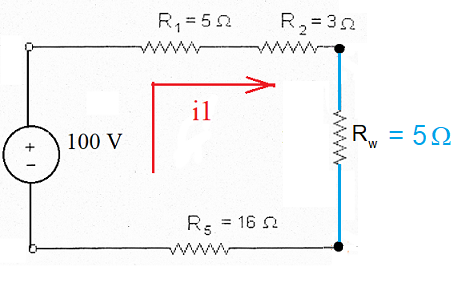
Agora fica mais fácil encontrar a corrente da fonte porque, uma vez resolvido o paralelo, o circuito fica reduzido a um circuito série:

Equiv2.png

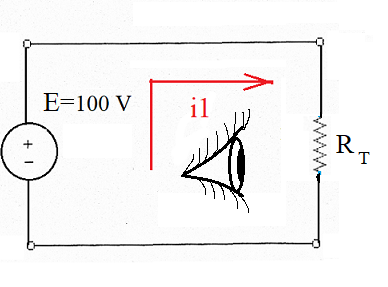
Ou, sob o ponto de vista da fonte:

Equival4.png

E a corrente da fonte I1 será dada por:

I1 = E/(RT )

, onde RT = R1 + R2 + Rw + R5 = 5 + 3 + 5 + 16 = 29 Ω

I1 = 100/29

→ I1 = 3,45 Ω

Ora, agora para calcular as correntes individuais Isub>2 e Isub>3 do paralelo, basta calcular qual a tensão VAB, a qual será dada por:

VAB = Rw.I1 = 5. 3,45 = 17,24 V

Equival3.png

Esta tensão, obviamente, será igual à

VAB = (R6 + R7).I2 e a

VAB = (R3 + R4).I3

Assim, a corrente I2 será dada por:

I2 = VAB/(R6 + R7) = 17,24/(8 + 2)

I2 = 17,24/10 → I2 = 1,72 A

E a corrente I3, por sua vez, será dada por:

I3 = VAB/(R3 + R4) = 17,24/(4 + 6)

I3 = 17,24/10 → I3 = 1,72 A

Como quisemos demonstrar!!!!!!

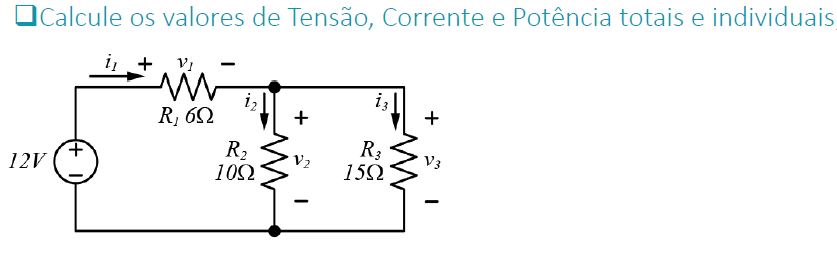
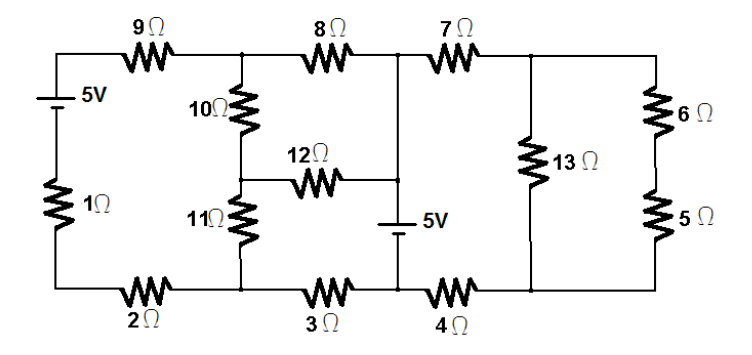
Exercício 1

Resolva o circuito abaixo utilizando as Leis de Kirchoff e Lei de Ohm:

Circmisto1.png

Solução do Exercício de Leis de Kirchoff

Análise de Malhas Generalizada

Os métodos de análise por inspeção, que utilizam Leis de Kirchoff e Lei de Ohm são bastante eficientes, mas dependem muito da expertise do profissional que está analisando o circuito.

A análise de malhas generalizada é um método sistemático que permite analisar qualquer circuito, através das suas correntes internas.

É mais apropriada para análise de circuitos com poucas malhas e com fontes de tensão, ao invés de fontes de corrente!

Não depende de identificar qual(is) o(s) melhor(es) equacionamento(s), mas apenas da aplicação correta do método.

O método consiste nos seguintes passos:


.

→ Para cada malha, faça:
  1. Arbitre uma corrente elétrica percorrendo toda aquela malha, e não para os ramos individuais, como fazíamos;
  2. Seguindo o sentido desta corrente, compute o somatório das tensões (fontes e quedas de tensões nos resistores) da seguinte maneira:
    1. A tensão da fonte de tensão será dada pelo valor da fonte e o sinal de entrada da corrente na fonte;
    2. Em ramos isolados, a queda de tensão será dada por R.Ix, onde Ix é a corrente daquela malha;
    3. Em ramos comuns a duas malhas, a queda de tensão será dada por R.(Ix - Iy), onde Ix é a corrente daquela malha, e Iy, a corrente da outra malha;
    4. Em fontes de corrente, arbitre uma tensão e depois utilize o valor da fonte para determinar a corrente naquele ramo;
  3. Iguale o somatório a zero.
→Repita o procedimento para as demais malhas.
→Resolva o sistema de equações por substituição, ou inversão de matrizes e encontre as correntes das malhas.
→As correntes dos ramos comuns à duas malhas serão calculados como a diferença entre as correntes de malhas.
→Determine as tensões de interesse.


 * Você pode escolher o sentido horário, ou antihorário, porque, caso o sentido inicial tenha sido arbitrado errado, o sinal da corrente resultará em negativo, indicando que o sentido é o inverso. PORÉM, é extremamente recomendável que o sentido arbitrado para TODAS AS CORRENTES seja O MESMO: ou horário, ou anti-horário, sob pena de duas correntes terem seus sentidos arbitrados errado, e o erro de uma anular o erro da outra.

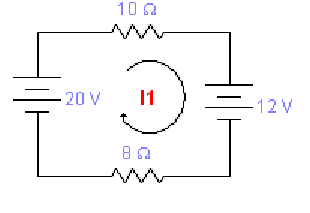
Exemplo 1: Análise de Malhas para circuito série

Analmalhas2.png

Como este circuito só contém uma malha, a análise se dará como segue:

1) Arbitre uma corrente elétrica percorrendo toda aquela malha 

→ Ok! Arbitrada a corrente I1;

2) Seguindo o sentido desta corrente, compute o somatório das tensões. 

→ -20 + 10.I1 +12 +8.I1 = 0

3)Resolva a equação. 

→ 18.I1 = 20 - 12 → 18.I1 = 8 → I1 = 8/18 

 → I1 = 0,44 A

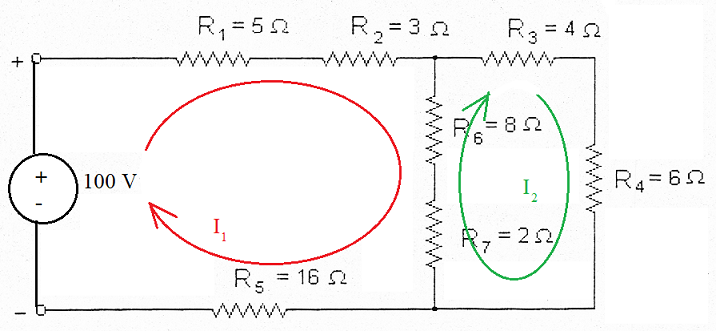
Exemplo 2: Análise de Malhas para circuito misto 1

Analmalhas3.png

Este circuito contém duas malhas, então, a análise se dará como segue:

1) Arbitre uma corrente elétrica em cada malha 

→ Ok! Arbitradas as correntes I1 e I2;

2.1) Seguindo o sentido da corrente I1, compute o somatório das tensões na malha 1:

- 100 + R1.I1 + R2.I1 + R6.(I1 -I2) + R7.(I1 -I2) + R5.I1 = 0

Ou seja:

- 100 + 5.I1 + 3.I1 + 8.(I1 -I2) + 2.(I1 -I2) + 16.I1 = 0

- 100 + 8.I1 + 8.I1 -8. I2 + 2.I1 -2. I2 + 16.I1 = 0

- 100 + 34.I1 -10. I2 = 0 

34.I1 -10.I2  = 100 (Equação I)

2.2) Seguindo o sentido da corrente I2, compute o somatório das tensões na malha 2:

R7.(I2 -I1) + R6.(I2 -I1) + R3.I2 + R4.I2 = 0

Ou seja:

2.(I2 -I1) + 8.(I2 -I1) + 4.I2 + 6.I2 = 0

2.I2 - 2.I1 + 8.I2 -8.I1 + 4.I2 + 6.I2 = 0

- 10.I1 + 20.I2 = 0

20.I2 = 10.I1 


2.I2 = I1 (Equação II)


3)Resolva o sistema de equações 

→ 34.I1 -10.I2  = 100 

 → 2.I2 = I1

Existem várias maneiras de se resolver um sistema de equações. Por exemplo:

3.1) Por substituição:

Fazendo I1 = 2.I2 e substituindo-se em: 34.I1 -10.I2 = 100, teremos:

34.(2.I2) - 10.I2 = 100

68.I2 - 10.I2 = 100

58.I2 = 100

I2 = 100/58

→ I2 = 1,72 A

E, por consequência:

I1 = 2.I2

I1 = 2.1,72

→ I1 = 3,44 A

3.2) Resolvendo o sistema de equações por soma:

Sistequ1.png

E, assim por diante.

4) A corrente I3 será dada por I1 - I2 , portanto, 3,44 - 1,72 = 1,72 A


Exemplo 3: Análise de Malhas para circuito misto 2

Analmalhas5.png


Este circuito contém duas malhas, então, a análise se dará como segue:

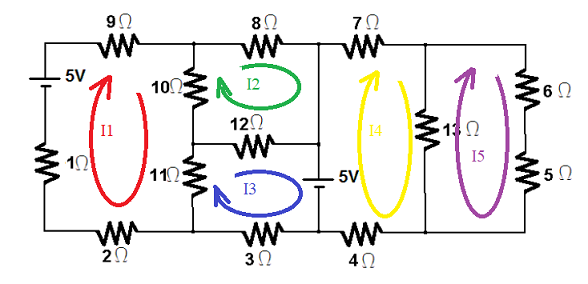
Passo 1. Arbitrando as correntes de malha

Analmalhas5-1.png


Passo 2. Levantando as tensões das malhas

2.1) Seguindo o sentido da corrente I1, compute o somatório das tensões na malha 1:

2.I1 + 1.I1 -5 + 9.I1 + 10.(I1 - I2) + 11.(I1 -I3) = 0

33.I1 - 10.I2 - 11.I3 = 5 (Equação I)

2.2) Seguindo o sentido da corrente I2, compute o somatório das tensões na malha 2:

10.(I2 -I1) + 8.I2 + 12.(I2 - I3) = 0

- 10.I1 + 30.I2 - 12.I3 = 0 (Equação II)


2.3) Seguindo o sentido da corrente I3, compute o somatório das tensões na malha 3:

11.(I3 -I1) + 12.(I3 -I2) +5 + 3.I3 = 0

- 11.I1 -12.I2 +26.I3 = -5 (Equação III)


2.4) Seguindo o sentido da corrente I4, compute o somatório das tensões na malha 4:

-5 + 7.I4+ 13.(I4 -I5) + 4.I4 = 0

24.I4 - 13.I5 = 5 (Equação IV)


2.5) Seguindo o sentido da corrente I5, compute o somatório das tensões na malha 5:

13.(I5 -I4) + 6.I5 + 5.I5 = 0

-13.I4 +24.I5 = 0 (Equação V)

Passo 3: Resolvendo o sistema de equações

Estas foram as equações identificadas: 


(I)   33.I1 - 10.I2 - 11.I3 = 5 
(II)  -10.I1 + 30.I2  - 12.I3 = 0
(III) -11.I1 -12.I2  +26.I3 = -5
(IV)   24.I4 - 13.I5  = 5
(V)   -13.I4 +24.I5  = 0

Vamos começar pelas equações (I), (II) E (III), que se relacionam entre si e resolvê-las aqui utilizando o Método da Substituição:

De (I), fazendo I1 = (5 + 10.I2 + 11.I3)/33, e substituindo em (II) e em (III):

-10.(5/33 + 10/33.I2 + 11/33.I3)+ 30.I2 - 12.I3 = 0

- 3,03.I2 - 3,33.I3 + 30.I2 - 12.I3 = 1,51 

(VI) 26,97.I2 - 15,33.I3 = 1,51


-11.(5/33 + 10/33.I2 + 11/33.I3 ) -12.I2 +26.I3 = -5

-55/33 -110/33.I2 - 121/33.I3 -12.I2 +26.I3 = -3,333 

(VII)-15,333.I2  +22,333.I3 = -3,333


Multiplicando (VI) por 1,4565 e somando com (VII):

39,28.I2 -22,333.I3 = 2,2

-15,333.I2 +22,333.I3 = -3,333 +

23,95.I2 + 0 = -1,1333

I2 = -1,1333/23,95

→ I2 = -0,04732 A = -47,32 mA


Substituindo I2 em (VI):

26,97.(-0,04732) - 15,33.I3 = 1,51

-1,27 - 15,33.I3 = 1,51

-15,33.I3 = 2,786

→ I3 = -0,18175 = -181,75 mA


Por fim, substituindo I2 e I3 em (I):

33.I1 - 10.(-0,04732) - 11.(-0,18175) = 5

33.I1 + 0,4732 + 2 = 5

33.I1 = 2,52755

→ I1 = 0,0766 = 76,6 mA


Agora, vamos investigar as duas correntes restantes: 

  24.I4 - 13.I5 = 5
 -13.I4 +24.I5  = 0

Multiplicando-se a segunda equação por 1,846:

24.I4 -13.I5 = 5

-24.I4 +44,3.I5 = 0

0 + 31,3.I5 = 5

I5 = 5/31,3

→ I5 = 0,159A = 159 mA

Substituindo-se em (IV):

24.I4 -13.0,159 = 5

24.I4 = 5 + 2,0766

→ I4 = 0,295A = 295 mA

Análise Computacional de circuitos

Note que, todos os sistemas de equações que resolvemos até agora podem ser organizados como matrizes.

Note que todos os sistemas de equações em análise de malha tomam a seguinte forma: 

 +R11.I1 - R12.I2 - R13.I3 - R14.I4  ... - R1n.In = Vx
 -R21.I1 + R22.I2 - R23.I3 - R24.I4  ... - R2n.In = Vy
 ...
 -Rn1.I1 - Rn2.I2 - Rn3.I3 - Rn4.I4  ... + Rnn.In = Vw

onde Rii é a soma das resistências da malha i (também chamada de resistência própria da malha) e Rij é a resistência entre a malha i e a malha j (ou resistência mútua a i e a j).


Todas estas equações podem ser separadas como: 

 |   R11  -R12  -R13  -R14  ... -R1n  |     | I1 |             | Vx |
 |   R21  -R22  -R23  -R24  ... -R2n  |     | I2 |             | Vy |
 |   ...                              | .   | ... |   =  | ... |  
 |   Rn1  -Rn2  -Rn3  -Rn4  ... -Rnn  |     | In |             | Vw |

ou 

  R . I = V

onde:

  • R é a matriz de resistências, de ordem nxn do circuito, onde n é o número de correntes de malha;
  • I é a matriz de correntes arbitradas nas malhas, de ordem nx1, e
  • V é a matriz de fontes de tensão das malhas, também de ordem nx1.


As resistências Rii da diagonal principal da matriz sempre têm valor positivo, e as mútuas Rij (devido à diferença de sentido das correntes em malhas distintas), sempre entram com valor negativo.

Além disto, a matriz de resistências R é sempre uma matriz quadrada e simétrica. Esta matriz também, normalmente, é esparsa, o que torna sua análise ainda mais fácil.

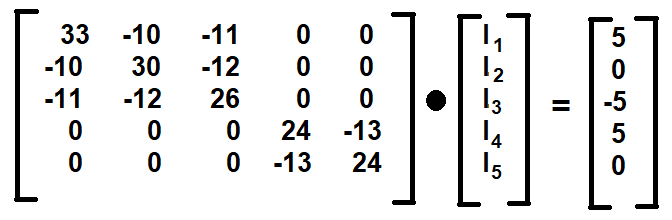
No caso deste circuito:

Sistmatrix5.png


A diagonal principal desta matriz é a soma de todas as resistências ligadas ao nó.

As outras posições i,j, são as respectivas resistências que unem aquele nó i, ao nós j adjacentes, com sinal negativo!

A matriz de correntes I de malha é sempre uma matriz coluna, de ordem n x 1.


E a matriz de fontes de tensão de malha também é uma matriz coluna, de ordem n x 1.

Se você tiver acesso a algum aplicativo de cálculo, como Matlab ou Scilab, o qual é gratuito, ou mesmo à uma planilha de cálculo, como Excel, você pode resolver o sistema de equações de uma maneira MUITO mais fácil!

Usando inversão de matriz, todo cálculo se limitará a executar a seguinte operação matricial: 

I = V/R = (R)-1 x V

Assim, para resolver o sistema, deve-se seguir os seguintes passos:

  1. Digitar a matriz R;
  2. Inverter a matriz R, criando Rinv;
  3. Digitar a matriz V;
  4. Executar a multiplicação de Rinv por V

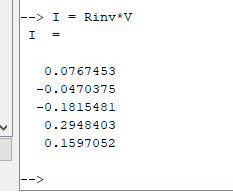
Para este circuito, fizemos o cálculo utilizando o Scilab, desta forma:


No Matlab ou Scilab 

> R = [33 -10 -11 0 0 
-10 30 -12 0 0
-11 -12 26 0 0
0 0 0 24 -13
0 0 0 -13 24]

> V = [5
 0
-5
5
0]

> Ri = inv(R)

> I = Ri*V

ou:

Sistmatrix6.png
Sistmatrix7.png

Fontes Bibliográficas

COMISSÃO TRIPARTITE PERMANENTE DE NEGOCIAÇÃO DO SETOR ELÉTRICO NO ESTADO DE SÃO PAULO - CPN. Eletricidade Básica - Manual de treinamento curso básico segurança em instalações e serviços com eletricidade - NR 10 . Disponível em: https://portalidea.com.br/cursos/9f2909192195f210d6c6fa89c0894301.pdf

Lemes, Andryos da Silva. APOSTILA DE ELETRICIDADE BÁSICA. MINISTÉRIO DA EDUCAÇÃO, IFSP - CAMPUS DE PRESIDENTE EPITÁCIO. Disponível em:https://pt.scribd.com/document/280039386/Apostila-Eletricidade-Basica

ROCHA, Helder da. Introdução à Eletrônica para Artistas. Apostila de curso livre. 2017. Disponível em: http://www.argonavis.com.br/cursos/eletronica/IntroducaoEletronicaArtistas.pdf.

SAMBAQUI, ANA BARBARA KNOLSEISEN; TAQUES, BÁRBARA OGLIARI. Apostila de Eletricidade. MINISTÉRIO DA EDUCAÇÃO - IFSC - CAMPUS JOINVILLE. Joinville, agosto, 2010. Disponível em: http://wiki.itajai.ifsc.edu.br/images/c/c1/Apostila_de_Eletricidade_IFSC_JOINVILE.pdf

Souza, Giovani Batista. ELETRICIDADE. MINISTÉRIO DA EDUCAÇÃO - IFSC - CAMPUS ARARANGUÁ. Edição: fev, 2009. Disponível em: https://wiki.sj.ifsc.edu.br/images/e/e6/Aru-2009-Agosto-eletricidade_basica.pdf


<<< Voltar para página principal do curso

Leis de Kirchoff << AULA 10 - ANÁLISE DE MALHAS Análise de Nós >>
Disponível em “https://wiki.ifsc.edu.br/index.php?title=AULA_10_-_Eletricidade_Básica_-_FIC&oldid=22356”