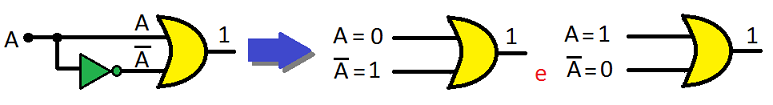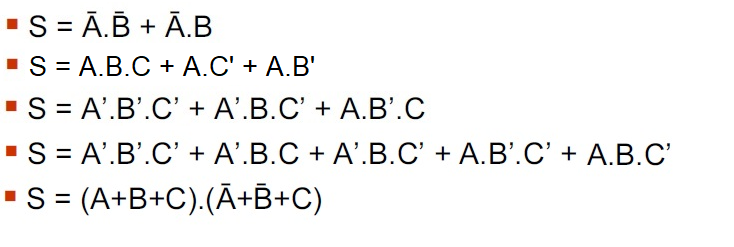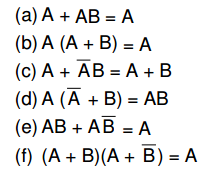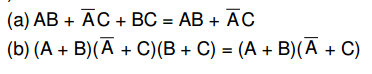AULA 5 - Eletrônica Digital 1 - Graduação

De IFSC
Revisão de 15h16min de 20 de setembro de 2016 por imported>Fargoud (→‎Exercícios propostos)
Ir para navegação Ir para pesquisar

<<= Voltar para a página principal do curso

Lógica Booleana

Infelizmente, apenas funções lógicas elementares podem ser implementadas utilizando-se poucos gates.

Além disto, vários circuitos distintos podem levar à mesma saída, para as mesmas entradas.

Então, como projetar o circuito ótimo, que vai utilizar menos portas, menos circuitos integrados (CIs), ocupar menos espaço, consumir menos energia, e mesmo assim satisfazer a função lógica que se deseja implementar???

A resposta para esta questão é exatamente o que a Álgebra Booleana tenta responder!!!!

As seções seguintes mostram que diferentes circuitos lógicos digitais podem responder exatamente do mesmo modo, às mesmas entradas e servem, principalmente, para ilustrar como o uso da lógica booleana pode REDUZIR os circuitos, em tamanho, volume, peso e custo.

Outro ponto importante, é que conhecer álgebra booleana te dá muita flexibilidade no projeto de circuitos, porque você pode substituir facilmente aquele componente que não tem disponível, no momento, por outro componente ou circuito equivalente!

É importante também o aluno entender que NÃO EXISTE uma receita de bolo para redução/simplificação de circuitos, utilizando-se lógica booleana. Quanto mais teoremos você conhecer, mais provável que vá conseguir chegar ao circuito ótimo. Mas não há uma sequência fixa de aplicação de teoremas que assegure chegar-se ao resultado ideal.

É fundamental a expertise do projetista, nesta tarefa!!!! :)

Postulados

A Álgebra booleana baseia-se na manipulação de variáveis booleanas, as quais só podem assumir valores binários (0 ou 1).

Os principais postulados da álgebra booleana são:

Tabelapostulados.jpg

Através das tabelas-verdade de cada operação lógica, é possível compreender-se e verificar-se os postulados.



TEOREMA 1:

A + 0 = A    →     0 + 0 = 0      e     1 + 0 = 1

tendo-se em vista que A, variável booleana, só pode assumir valor 0 ou 1.

Graficamente:

Teorema1.jpg

Pela tabela-verdade:

A 0 A+0
0 0 0
1 0 1



TEOREMA 2:

A + 1 = 1     →     0 + 1 = 1       e       1 + 1 = 1

tendo-se em vista que A, variável booleana, só pode assumir valor 0 ou 1.

Graficamente:

Teorema2.jpg

Pela tabela-verdade:

A 1 A+1
0 1 1
1 1 1



TEOREMA 3:

A + A = A     →     0 + 0 = 0       e       1 + 1 = 1

tendo-se em vista que A, variável booleana, só pode assumir valor 0 ou 1.

Graficamente:

Teorema3.jpg

Pela tabela-verdade:

A A A+A
0 0 0
1 1 1



TEOREMA 4:

A + A' = 1     →     0 + 1 = 1       e       1 + 0 = 1

tendo-se em vista que A, variável booleana, só pode assumir valor 0 ou 1.

Graficamente:

Teorema4.jpg

Pela tabela-verdade:

A A' A+A'
0 1 1
1 0 1



TEOREMA 5:

A . 0 = 0      →     0 . 0 = 0     e      1 . 0 = 0

tendo-se em vista que A, variável booleana, só pode assumir valor 0 ou 1.

Graficamente:

Teorema5.jpg

Pela tabela-verdade:

A 0 A.0
0 0 0
1 0 0



TEOREMA 6:

A . 1 = A       →     0 . 1 = 0       e       1 . 1 = 1

tendo-se em vista que A, variável booleana, só pode assumir valor 0 ou 1.

Graficamente:

Teorema6.jpg
A 1 A.1
0 1 0
1 1 1



TEOREMA 7:

A . A = A       →     0 . 0 = 0       e       1 . 1 = 1

tendo-se em vista que A, variável booleana, só pode assumir valor 0 ou 1.

Graficamente:

Teorema7.jpg

Pela tabela-verdade:

A A A.A
0 0 0
1 1 1



TEOREMA 8:

A . A' = 0       →     0 . 1 = 0       e       1 . 0 = 0

tendo-se em vista que A, variável booleana, só pode assumir valor 0 ou 1.

Graficamente:

Teorema08.jpg


Pela tabela-verdade:

A A' A.A'
0 1 0
1 0 0



TEOREMA 9:

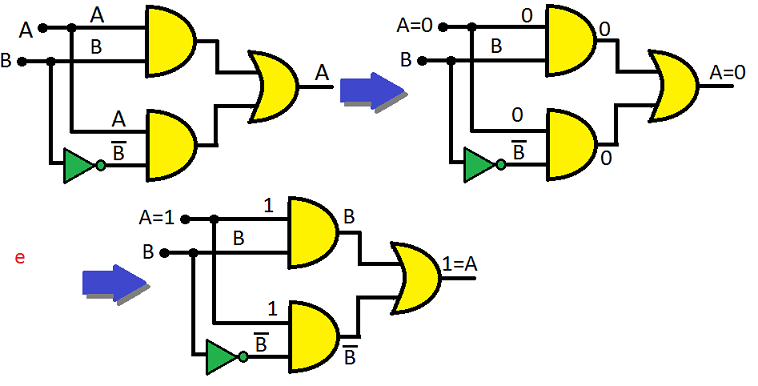
A + (A.B) = A       →     0 + (0.B) = 0 + 0 = 0      e       1 + (1.B) = 1 + B = 1

Demonstração: 

Fatorando-se a equação:   A + A.B  →   A.(1 + B)

Aplicando-se a propriedade 2:  A.(1) 
Aplicando-se a propriedade 5:  A

como quisemos demonstrar (c.q.d.)!


Graficamente:

Teorema9.jpg


Pela tabela-verdade:

A B A.B A+A.B
0 0 0 0
0 1 0 0
1 0 0 1
1 1 1 1



TEOREMA 10:

A .(A + B) = A       →     0 .(0 + B) = 0.B = 0      e       1 .(1 + B) = 1.1 = 1

Demonstração: 

Efetuando-se a multiplicação (propriedade distributiva):   A . (A + B)  →   A.A + A.B

Aplicando-se a propriedade 7:  A + A.B 
Aplicando-se a propriedade 9:  A

como quisemos demonstrar (c.q.d.)!


Graficamente:

Teorema10.jpg

Pela tabela-verdade:

A B A+B A.(A+B)
0 0 0 0
0 1 1 0
1 0 1 1
1 1 1 1



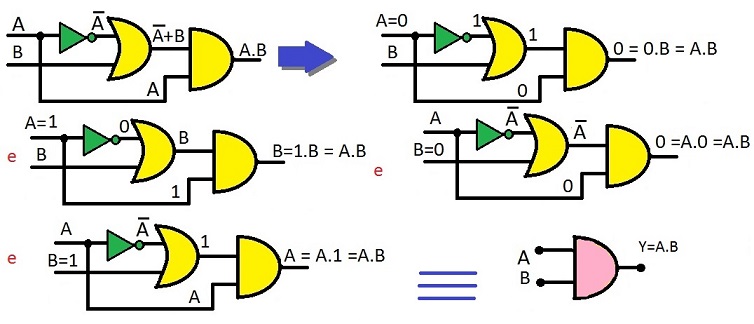
TEOREMA 11:

A.B + A.B' = A       →     0.B + 0.B' = 0 + 0 = 0        e     1.B + 1.B' = B + B' = 1

Demonstração: 

Efetuando-se a fatoração:   A.B + A.B'  →   A.(B + B')
Aplicando-se a propriedade 4:  A.(1)
Aplicando-se a propriedade 5:  A

como quisemos demonstrar (c.q.d.)!


Graficamente:

Teorema11.jpg

Pela tabela-verdade:

A B A.B A.B' A.B+A.B'
0 0 0 0 0
0 1 0 0 0
1 0 0 1 1
1 1 1 0 1



TEOREMA 12:

(A + B).(A + B') = A     →     (0 + B).(0 + B') = B.B' = 0      e       (1 + B).(1 + B') = 1.1 = 1

Demonstração: 

Efetuando-se a multiplicação (propriedade distributiva):   (A + B).(A + B')  →   A.A + A.B' + B.A + B.B'

Aplicando-se a propriedade 7:  A + A.B' + A.B + B.B'
Aplicando-se a propriedade 8:  A + A.B' + A.B + 0 = A + A.B' + A.B
Aplicando-se a fatoração: A.(1 + B' + B)
Aplicando-se as propriedades 2 (ou a 4): A.(1) 
Aplicando-se a propriedade 5:  A

como quisemos demonstrar (c.q.d.)!


Graficamente:

Teorema12.jpg

Pela tabela-verdade:

A B A+B A+B' (A+B).(A+B')
0 0 0 1 0
0 1 1 0 0
1 0 1 1 1
1 1 1 1 1



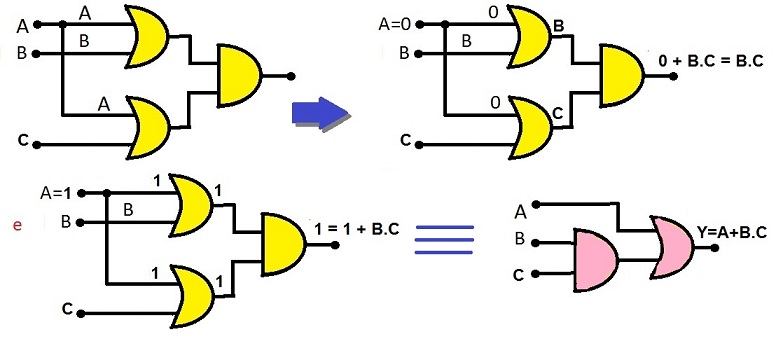
TEOREMA 13:

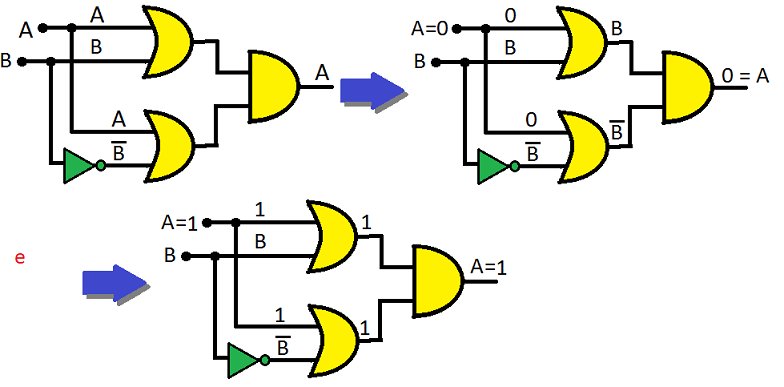
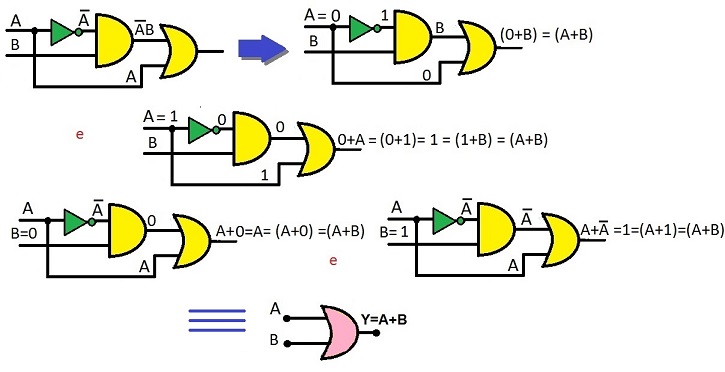
A + A'.B = A + B

Demonstração: 

Da propriedade 5 pode-se dizer que:    A + A'.B    →    A.1 + A'.B
Da propriedade 4 pode-se dizer que: A.(B + B') + A'.B
Aplicando-se a propriedade distributiva:  A.B + A.B' + A'.B  
Da propriedade 3 pode-se dizer que:  A.B + A.B + A.B' + A'.B
Aplicando-se a fatoração: A.(B' + B) + B.(A + A')
Aplicando-se a propriedade 4: A.(1) + B.(1)
Aplicando-se a propriedade 5: A + B

como quisemos demonstrar (c.q.d.)!


Graficamente:

Teorema013.jpg

Pela tabela-verdade:

A B A' A'.B A + A'.B A+B
0 0 1 0 0 0
0 1 1 1 1 1
1 0 0 0 1 1
1 1 0 0 1 1



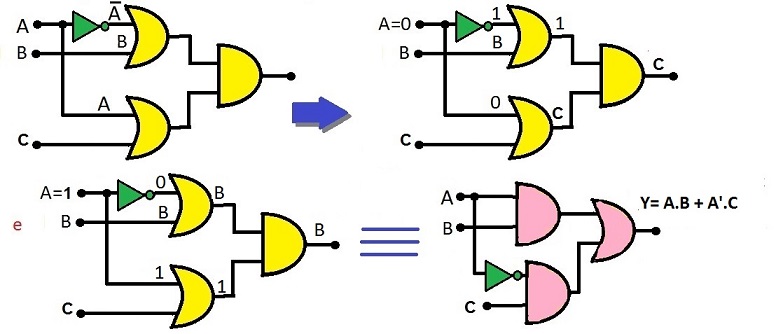
TEOREMA 14:

A .(A' + B) = A.B

Demonstração: 

Efetuando-se a multiplicação (propriedade distributiva):   A . (A' + B)  →   A.A' + A.B
Aplicando-se a propriedade 8:  0 + A.B 
Aplicando-se a propriedade 1:  A.B

como quisemos demonstrar (c.q.d.)!


Graficamente:

Teorema14.jpg

Pela tabela-verdade:

A B A' A'+B A.(A'+B) A.B
0 0 1 1 0 0
0 1 1 1 0 0
1 0 0 0 0 0
1 1 0 1 1 1



TEOREMA 15:

(A + B).(A + C) =  A + B.C

Note que esta proposição, ao contrário das outras, envolve 3 VARIÁVEIS BOOLEANAS, o que não é nada demais, mas exige um pouco mais de atenção.

Variáveis booleanas, como já foi descrito, nada mais são do que pontos do circuito aonde você tem que controlar os níveis de tensão. Podem ser entradas de algum componente, ou até do próprio projeto em si, ou saídas. O que diferencia este teorema dos outros, é que envolve 3 parâmetros de uma só vez; não apenas dois.

Além do circuito ter mais uma entrada, a sua Tabela-Verdade tem que ser construída de forma distinta.

Veja neste link, como construir-se TVs de 3 ou mais variáveis: Tabelas-verdade de 3 variáveis

Demonstração: 

Efetuando-se a multiplicação (propriedade distributiva):   (A + B).(A + C)  →   A.A + A.C + B.A + B.C
Aplicando-se a propriedade 7:  A + A.C + A.B + B.C 
Aplicando-se a propriedade 5:  A.1 + A.C + A.B + B.C
Extraindo-se A dos termos:  A.(1 + C + B) + B.C
Aplicando-se a propriedade 2: A.(1) + B.C
Aplicando-se a propriedade 5:  A + B.C

como quisemos demonstrar (c.q.d.)!


Graficamente:

Teorema15.jpg

Pela tabela-verdade:

A B C A+B A+C (A+B).(A+C) B.C A+B.C
0 0 0 0 0 0 0 0
0 0 1 0 1 0 0 0
0 1 0 1 0 0 0 0
0 1 1 1 1 1 1 1
1 0 0 1 1 1 0 1
1 0 1 1 1 1 0 1
1 1 0 1 1 1 0 1
1 1 1 1 1 1 1 1


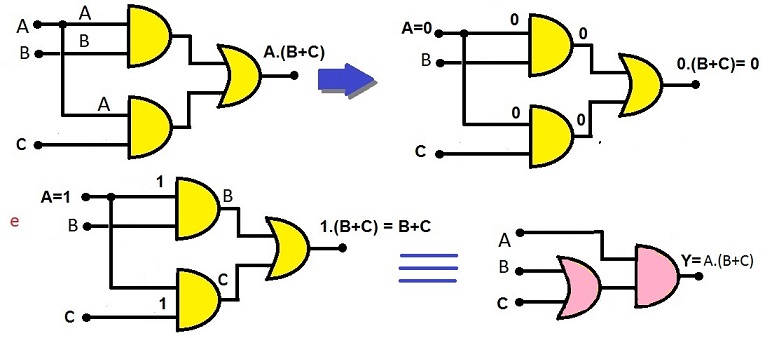
TEOREMA 16:

 A.B + A.C = A.(B+C)      →     0.B + 0.C = 0.(B+C) = 0      e       1.B + 1.C = 1.(B+C) = B + C

Demonstração: 

Efetuando-se a fatoração:   A.B + A.C   →     A.(B + C)


como quisemos demonstrar (c.q.d.)!


Graficamente:

Teorema16.jpg


Pela tabela-verdade:

A B C A.B A.C A.B + A.C B+C A.(B+C)
0 0 0 0 0 0 0 0
0 0 1 0 0 0 1 0
0 1 0 0 0 0 1 0
0 1 1 0 0 0 1 0
1 0 0 0 0 0 0 0
1 0 1 0 1 1 1 1
1 1 0 1 0 1 1 1
1 1 1 1 1 1 1 1



TEOREMA 17:

A.B + A'.C = (A + C).(A' + B)     →     0.B + 1.C = (0 + C).(1 + B) = C     e   1.B + 0.C =  (1 + C).(0 + B) = B

Demonstração: 

Efetuando-se a multiplicação (propriedade distributiva):   (A + C).(A' + B)   →   A.A' + A.B + A'.C + B.C
Aplicando-se o teorema 8: 0 + A.B + A'.C + B.C = A.B + A'.C + B.C
Aplicando-se o teorema 5: A.B + A'.C + B.C.(1)
Aplicando-se o teorema 4: A.B + A'.C + B.C.(A + A')
Efetuando-se a multiplicação (distributiva): A.B + A'.C + A.B.C + A'.B.C
Efetuando-se a fatoração dos termos comuns: A.B.(1 + C) + A'.C.(1 + B)
Aplicando-se o teorema 2: A.B.(1) + A'.C.(1)
Aplicando-se o teorema 5: A.B + A'.C

como quisemos demonstrar (c.q.d.)!



Graficamente:

Teorema17.jpg

Pela tabela-verdade:

A B C A' A.B A'.C A.B + A'.C A+C A'+B (A+C).(A'+B)
0 0 0 1 0 0 0 0 1 0
0 0 1 1 0 1 1 1 1 1
0 1 0 1 0 0 0 0 1 0
0 1 1 1 0 1 1 1 1 1
1 0 0 0 0 0 0 1 0 0
1 0 1 0 0 0 0 1 0 0
1 1 0 0 1 0 1 1 1 1
1 1 1 0 1 0 1 1 1 1



TEOREMA 18:

(A + B).(A' + C) = A.C + A'.B     →  (0 + B).(1 + C) = B     e   (1 + B).(0 + C) = C

Demonstração: 

Efetuando-se a multiplicação (propriedade distributiva):   (A + B).(A' + C)   →   A.A' + A.C + A'.B + B.C
Aplicando-se o teorema 8: 0 + A.C + A'.B + B.C = A.C + A'.B + B.C
Aplicando-se o teorema 5: A.C + A'.B + B.C.(1)
Aplicando-se o teorema 4: A.C + A'.B + B.C.(A + A')
Efetuando-se a multiplicação (distributiva): A.C + A'.B + A.B.C + A'.B.C
Efetuando-se a fatoração dos termos comuns: A.C.(1 + B) + A'.B.(1 + C)
Aplicando-se o teorema 2: A.C.(1) + A'.B.(1)
Aplicando-se o teorema 5: A.C + A'.B

como quisemos demonstrar (c.q.d.)!



Graficamente:

Teorema18.jpg


Pela tabela-verdade:

A B C A' A+B A'+C (A+B).(A'+C) A.C A'.B A.C + A'.B
0 0 0 1 0 1 0 0 0 0
0 0 1 1 0 1 0 0 0 0
0 1 0 1 1 1 1 0 1 1
0 1 1 1 1 1 1 0 1 1
1 0 0 0 1 0 0 0 0 0
1 0 1 0 1 1 1 1 0 1
1 1 0 0 1 0 0 0 0 0
1 1 1 0 1 1 1 1 0 1



TEOREMA 19:

A.B + A'.C + B.C = A.B + A'.C  →  0.B + 1.C + B.C = C + B.C = C.(1 + B) = C  e  1.B + 0.C + B.C = B + B.C = B.(1 + C) = B

Demonstração: 

Aplicando-se o teorema 5: A.B + A'.C + B.C.(1)
Aplicando-se o teorema 4: A.B + A'.C + B.C.(A + A')
Efetuando-se a multiplicação (distributiva): A.B + A'.C + A.B.C + A'.B.C
Efetuando-se a fatoração dos termos comuns: A.B.(1 + B) + A'.C.(1 + C)
Aplicando-se o teorema 2: A.B.(1) + A'.C.(1)
Aplicando-se o teorema 5: A.B + A'.C

como quisemos demonstrar (c.q.d.)!


Graficamente:

Teorema19.jpg

Pela tabela-verdade:

A B C A' A.B A'.C B.C AB+A'C+BC AB+A'C
0 0 0 1 0 0 0 0 0
0 0 1 1 0 1 0 1 1
0 1 0 1 0 0 0 0 0
0 1 1 1 0 1 1 1 1
1 0 0 0 0 0 0 0 0
1 0 1 0 0 0 0 0 0
1 1 0 0 1 0 0 1 1
1 1 1 0 1 0 1 1 1



TEOREMA 20:

(A + B).(A' + C).(B + C) = (A + B).(A' + C)  →  (0 + B).(1 + C).(B + C) = B.1.B + B.1.C = B     e 
(1 + B).(0 + C).(B + C) = 1.C.B + 1.C.C = C

Demonstração: 

Efetuando-se a multiplicação (propriedade distributiva):   (A + B).(A' + C).(B + C) 
→   (A.A' + A.C + A'.B + B.C).(B + C) 
→   A.A'.B + A.A'.C + A.C.B + A.C.C + A'.B.B + A'.B.C + B.C.B + B.C.C
Aplicando-se o teorema 8: 0.B + 0.C + A.C.B + A.C.C + A'.B.B + A'.B.C + B.C.B + B.C.C 
= A.C.B + A.C.C + A'.B.B + A'.B.C + B.C.B + B.C.C
Aplicando-se o teorema 7: A.C.B + A.C + A'.B + A'.B.C + B.C + B.C
Fatorando-se os termos comuns: A.C.(B + 1) + A'.B.(1 + C) + B.C.(1 + 1) 
Aplicando-se o teorema 2: A.C + A'.B + B.C
que é igual a (A + B).(A' + C), após a multiplicação dos fatores


como quisemos demonstrar (c.q.d.)!


Graficamente:

Teorema20.jpg


Pela tabela-verdade:

A B C A' A+B A'+C B+C (A+B)(A'+C)(B+C) (A+B)(A'+C)
0 0 0 1 0 1 0 0 0
0 0 1 1 0 1 1 0 0
0 1 0 1 1 1 1 1 1
0 1 1 1 1 1 1 1 1
1 0 0 0 1 0 0 0 0
1 0 1 0 1 1 1 1 1
1 1 0 0 1 0 1 0 0
1 1 1 0 1 1 1 1 1




Exercícios propostos

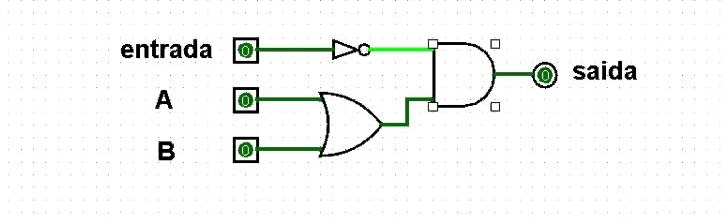
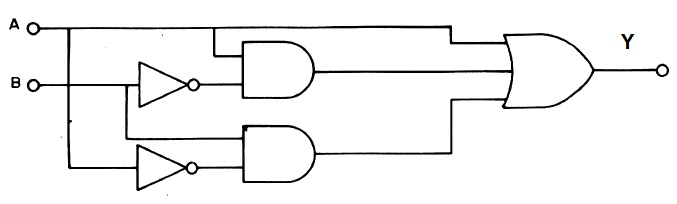
  1. No circuito abaixo, qual será a expressão para saída? Escreva também a tabela-verdade do circuito.
    Exerc1log.jpg
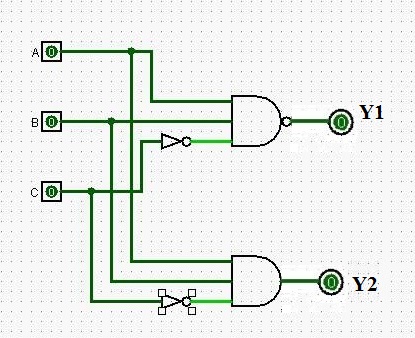
  2. No circuito abaixo, quais serão as saídas Y1 e Y2, para as entradas A = 0, B = 0 e C = 1. Escreva também a tabela-verdade do circuito.
    Exerc2log.jpg
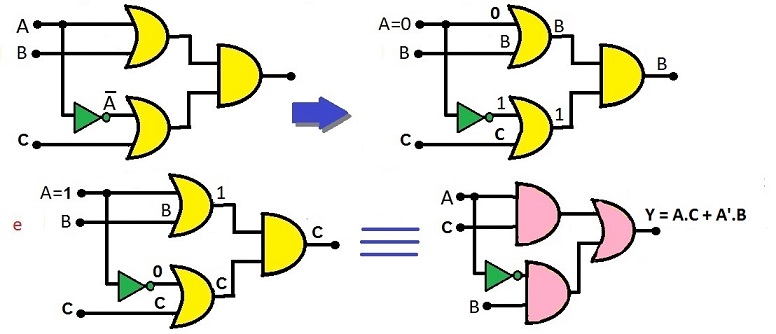
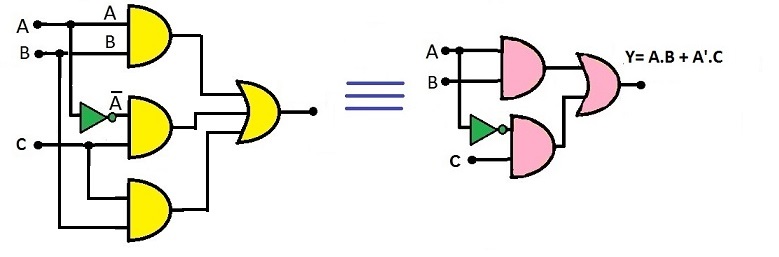
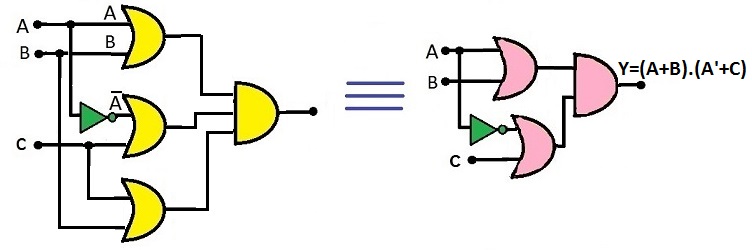
  3. Escreva a expressão de saída para o circuito abaixo e também a tabela-verdade que o descreve.
    Exerc3logs.jpg
  4. Utilizando os teoremas de Lógica Booleana, tente reduzir o circuito acima.
  5. Utilizando os teoremas de Lógica Booleana, tente minimizar o circuito Y = (A'.B + A.B').(A'.C + A.C')
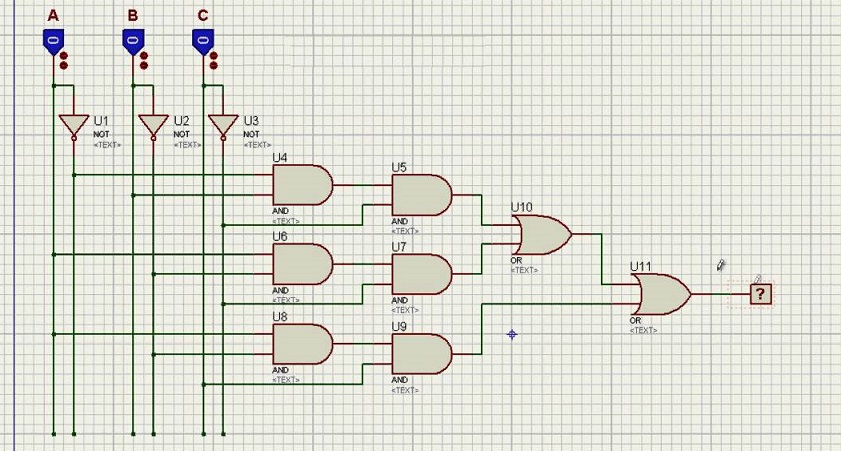
  6. Encontre a expressão que descreve o circuito abaixo e minimize-a, se possível. Em seguida, desenhe o circuito minimizado correspondente.
    Exerc6log.jpg
  7. Utilizando os teoremas de Lógica Booleana, tente minimizar as cinco expressões abaixo:
    Exerc5log.jpg
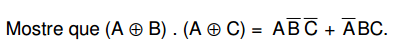
  8. Exercc5n8.jpg
  9. Demonstre os teoremas abaixo:
    Exercc5n10.jpg
  10. Demonstre os teoremas abaixo:
    Exercc5n11.jpg
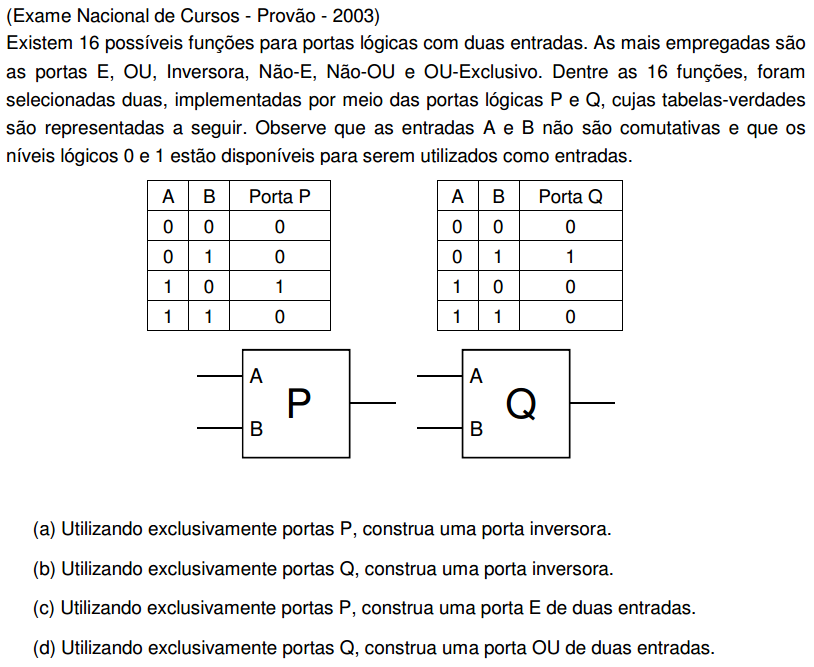
  11. Exercc5n12.jpg
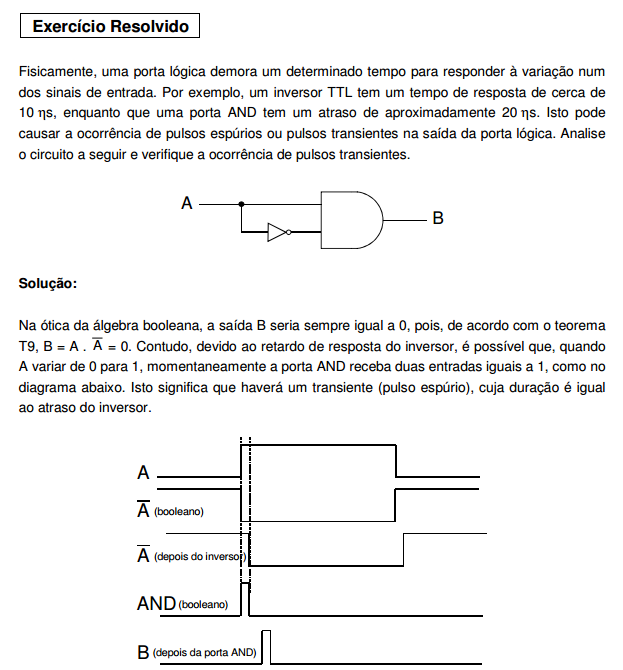
  12. Analise a resposta dos circuitos booleanos básicos no tempo:
    Exercc5n13.jpg
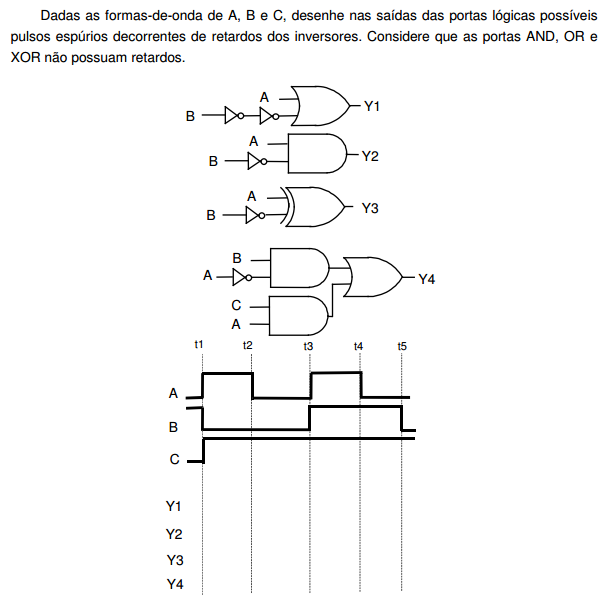
  13. Com base no exercício anterior, responda:
    Exercc5n14.jpg
<< Portas Lógicas Básicas AULA 5 - Lógica booleana >> Teoremas de De Morgan

<<= Página do curso

Disponível em “https://wiki.ifsc.edu.br/index.php?title=AULA_5_-_Eletrônica_Digital_1_-_Graduação&oldid=9989”